求最短路暂时掌握了4种,但感觉就dijkstra复杂度能用;
1 floyd算法:
就是暴力的三重循环,以每个点为中转点,每次遍历所有的点,看看能不能通过这个中转点更新最短路径;
优点:n<200时用这种方法,用邻接矩阵存图 ,可求任意的两点的最短路;而且好写;
缺点:复杂度太高,O(n^3)的复杂的,太多不必要的计算;

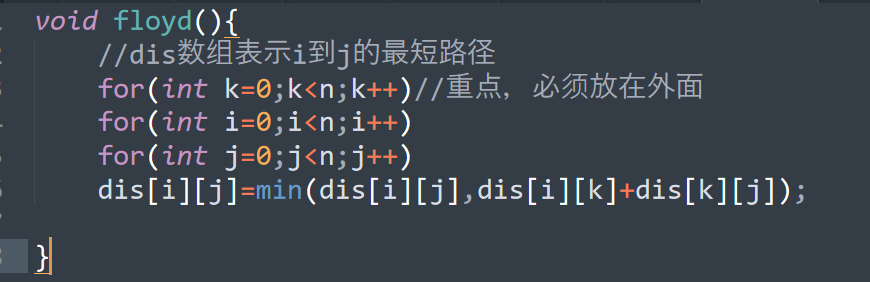
void floyd(){ //dis数组表示i到j的最短路径 for(int k=0;k<n;k++)//重点,必须放在外面 for(int i=0;i<n;i++) for(int j=0;j<n;j++) dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]); }
2 bellman-floyd算法:
解决单源最短路,就是循环n次,每次检查每一条边,看看是否能通过邻居更新最短的路径
优点:n<1e7可以考虑这种方法,用结构体数组存图即可,然后这是并行式计算,循环怎么搞都行,
缺点:复杂度还是蛮高的,每个点 O(n*m)的复杂度;

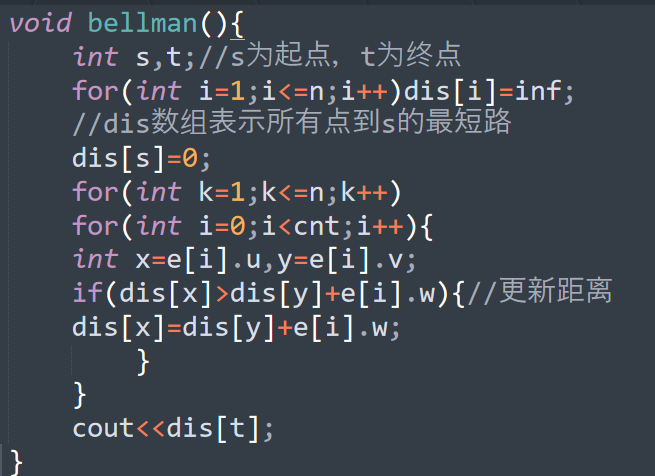
void bellman(){ int s,t;//s为起点,t为终点 for(int i=1;i<=n;i++)dis[i]=inf; //dis数组表示所有点到s的最短路 dis[s]=0; for(int k=1;k<=n;k++) for(int i=0;i<cnt;i++){ int x=e[i].u,y=e[i].v; if(dis[x]>dis[y]+e[i].w){//更新距离 dis[x]=dis[y]+e[i].w; } } cout<<dis[t]; }
3 SPFA :
缺点:不稳点,
算法:和广搜很像;
学了再更新;
4 dijkstra:
算法:基于贪心思想,就是每次更新之后,路径最短的那个点一定是最终的最短路径,因为借道去其他点必定比这个距离大;一次次迭代;
优点:考虑用邻接表存图,复杂度可以接受,而且稳定;解决单源最短路问题,复杂度O(m*log(n));

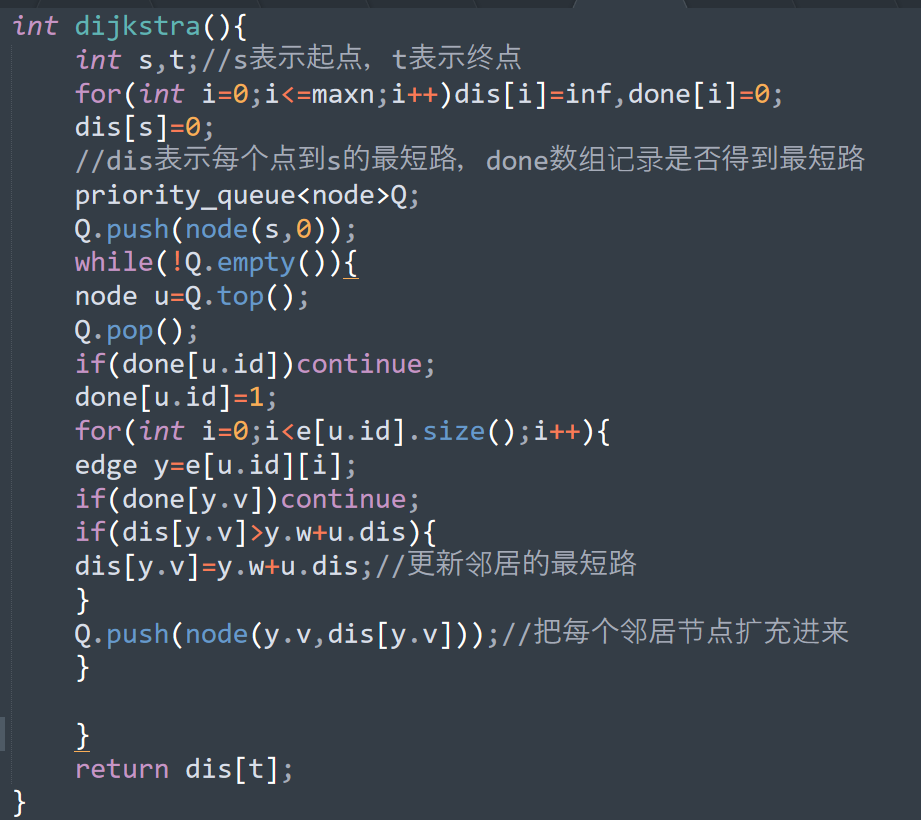
int dijkstra(){ int s,t;//s表示起点,t表示终点 for(int i=0;i<=maxn;i++)dis[i]=inf,done[i]=0; dis[s]=0; //dis表示每个点到s的最短路,done数组记录是否得到最短路 priority_queue<node>Q; Q.push(node(s,0)); while(!Q.empty()){ node u=Q.top(); Q.pop(); if(done[u.id])continue; done[u.id]=1; for(int i=0;i<e[u.id].size();i++){ edge y=e[u.id][i]; if(done[y.v])continue; if(dis[y.v]>y.w+u.dis){ dis[y.v]=y.w+u.dis;//更新邻居的最短路 } Q.push(node(y.v,dis[y.v]));//把每个邻居节点扩充进来 } } return dis[t]; }
判负圈的问题,学了再补充;
