题目链接:http://poj.org/problem?id=2135
今天学习最小费用流。模板手敲了一遍。
产生了一个新的问题:对于一条无向边,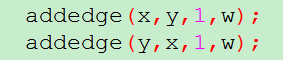 这样修改了正向边容量后,反向边不用管吗?
这样修改了正向边容量后,反向边不用管吗?
后来想了想,得出了个结论。路径所选的边只会包括正反中的一条。

#include <iostream> #include <cstdio> #include <cstring> #include <vector> #include <queue> #include <algorithm> using namespace std; const int maxn = 2e3; const int INF = 1e9; int dist[maxn]; int pv[maxn],pe[maxn]; struct edge { int to, cap, rev; int cost; edge(int a, int b, int c, int d) { to = a, cap = b, cost = c, rev = d; } }; vector<edge> g[maxn]; void addedge(int from,int to,int cap,int cost) { g[from].push_back(edge(to,cap,cost,g[to].size())); g[to].push_back(edge(from,0,-cost,g[from].size()-1)); } int n; int vis[maxn]; void SPFA(int s, int t) { for(int i = 1; i < maxn; i++) dist[i] = INF; memset(vis, 0, sizeof(vis)); dist[s] = 0, vis[s] = 1; queue<int> q; q.push(s); while(!q.empty()) { int u = q.front(); q.pop(); vis[u] = 0; for(int i = 0; i < g[u].size(); i++) { edge &e = g[u][i]; if(e.cap > 0 && (dist[e.to] - (dist[u] + e.cost)) > 0) { pv[e.to] = u, pe[e.to] = i; dist[e.to] = dist[u] + e.cost; if(!vis[e.to]) { vis[e.to] = 1; q.push(e.to); } } } } } int min_cost_flow(int s,int t,int f,int& max_flow) { int ret = 0.0; while(f>0) { SPFA(s, t); if(dist[t] == INF) return ret;///同一目的地,每次增广路都是最小费用 ///当所有边的流量都流净后,即没有残余网络,返回。 int d = f; for(int v=t;v!=s;v=pv[v]) { d = min(d,g[pv[v]][pe[v]].cap); } f -= d; max_flow += d; ret += (int)d*dist[t]; ///走一单位就消耗dist[t] for(int v=t;v!=s;v=pv[v]) { edge &e = g[pv[v]][pe[v]]; e.cap -= d; g[v][e.rev].cap += d; } } return ret; } int main() { int n,m; scanf("%d %d",&n,&m); int s=0,t=n+1; addedge(s,1,2,0); addedge(n,t,2,0); for(int i=1;i<=m;i++) { int x,y,w; scanf("%d %d %d",&x,&y,&w); addedge(x,y,1,w); addedge(y,x,1,w); } // printf("%d ",e[6].cap); ///反向边不用管它,因为路径只会选择正反里面的一条边 int maxflow = 0; int ans = min_cost_flow(s,t,INF,maxflow); for(int i = 0; i < maxn; i++) g[i].clear(); printf("%d ",ans); return 0; }
