2017.7.10~7.16
做好题
一题多解
自己多思考
第一种解法:快速幂。
F(x,m) mod k ≡ c可以转换为 x*(10^m-1)/9%k = c,进一步转换为x*(10^m-1)%(9*k) = 9*c%(9*k).

1 #include <iostream> 2 #include <cmath> 3 #include <algorithm> 4 #include <cstring> 5 using namespace std; 6 typedef long long ll; 7 ll quick_pow(ll a,ll m,ll mod) 8 { 9 ll res = 1; 10 while(m) 11 { 12 if(m%2) res = res*a%mod; 13 m /= 2; 14 a = a*a%mod; 15 } 16 return res; 17 } 18 int main() 19 { 20 int n,kase = 0; 21 cin>>n; 22 while(n--) 23 { 24 ll x,m,k,c; 25 cin>>x>>m>>k>>c; 26 ll mod = 9*k; 27 ll ans = quick_pow(10,m,mod); 28 if(ans==0) 29 { 30 ans = mod-1; 31 } 32 else 33 { 34 ans -= 1; 35 } 36 ll l1 = ans*x%mod; 37 ll l2 = c*9%mod; 38 cout<<"Case #"<<++kase<<":"<<endl; 39 if(l1==l2) 40 { 41 cout<<"Yes"<<endl; 42 } 43 else 44 { 45 cout<<"No"<<endl; 46 } 47 } 48 return 0; 49 }
第二种解法:矩阵快速幂
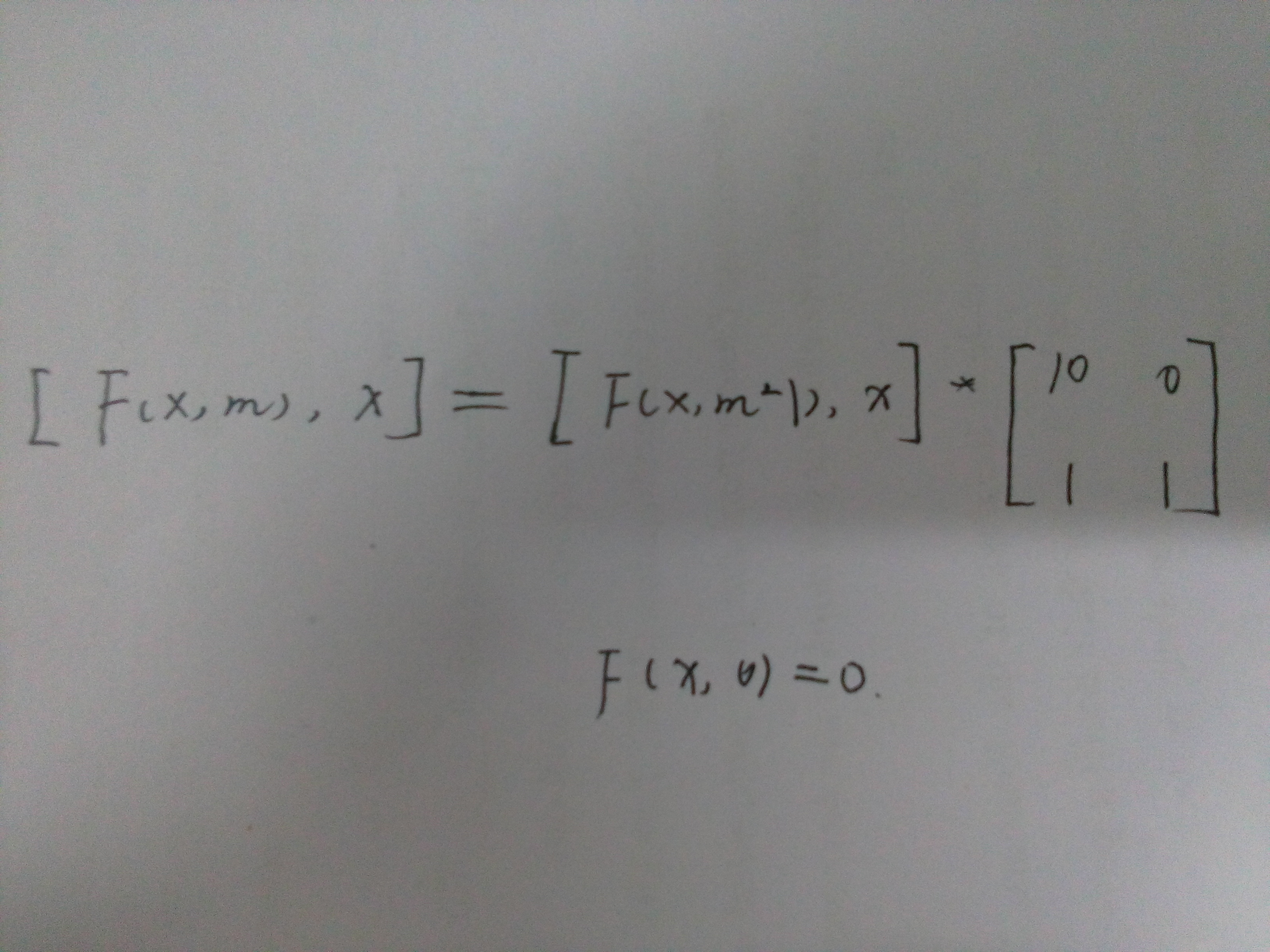
(不会在博客园上写公式,/(ㄒoㄒ)/~~)

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; struct matrix { int n; long long m[2][2]; }base,res; ll x,m,k,c; matrix multi(matrix a,matrix b) { matrix temp; memset(temp.m,0,sizeof(temp.m)); temp.n = a.n; for(int i=0;i<a.n;i++) { for(int j=0;j<b.n;j++) { for(int kk=0;kk<2;kk++) { temp.m[i][j] = (temp.m[i][j]+a.m[i][kk]*b.m[kk][j]%k)%k; } } } return temp; } ll quick_pow(ll n) { res.m[0][0] = 0,res.m[0][1] = x; res.n = 1; base.m[0][0] = 10,base.m[0][1] = 0; base.m[1][0] = 1,base.m[1][1] = 1; base.n = 2; while(n) { if(n%2) { res = multi(res,base); } n /= 2; base = multi(base,base); } return res.m[0][0]; } int main() { int T,kase = 0; cin>>T; while(T--) { cin>>x>>m>>k>>c; cout<<"Case #"<<++kase<<":"<<endl; if(quick_pow(m)==c) { cout<<"Yes"<<endl; } else { cout<<"No"<<endl; } } return 0; }
