Claris and XOR
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 332 Accepted Submission(s): 135
Problem Description
Claris
loves bitwise operations very much, especially XOR, because it has many
beautiful features. He gets four positive integers a,b,c,d that satisfies a≤b and c≤d. He wants to choose two integers x,y that satisfies a≤x≤b and c≤y, and maximize the value of x X. But he doesn't know how to do it, so please tell him the maximum value of x X.
Input
The first line contains an integer T——The number of the test cases.
For each test case, the only line contains four integers a,b,c,d. Between each two adjacent integers there is a white space separated.
For each test case, the only line contains four integers a,b,c,d. Between each two adjacent integers there is a white space separated.
Output
For each test case, the only line contains a integer that is the maximum value of x X.
Sample Input
2
1 2 3 4
5 7 13 15
Sample Output
6
11
Hint
In the first test case, when and only when $x=2,y=4$, the value of $x~XOR~y$ is the maximum.
In the second test case, when and only when $x=5,y=14$ or $x=6,y=13$, the value of $x~XOR~y$ is the maximum.
昨天的B题,我的理解力,我都惭愧了,自己写了好几个样例才完全搞懂。
从最高位到最低位贪心。
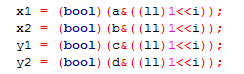
贪心时,如果x走到此地方
x y
b 1 1 0 0 0 d 1 0 0 1 1
a 1 0 0 0 0 c 1 0 0 0 1
此时x1 = x2, y1 =y2 而且x1 = y1,所以有唯一解,取 0. 如果y系列等于0 有唯一解 1
x y
b 1 0 1 0 1 1 d 1 0 0 0 0 0
a 1 0 0 0 0 c 1 0 0 0 0 0x1 != x2, y1 == y2,贪心使其为1. 如果y = 1,所以x = 0,此时二进制有五位数,设其为C, 所以10000 <= c <= 11111, 所以让b = ((ll)1<<i) - 1. 同理。
x y
b 1 0 1 0 1 1 d 1 0 0 0 0 0
a 1 0 0 0 0 c 0 1 0 0 0 0此时x1 != x2, y1 != y2, 0 1可任意取, 前面取 11111 后面取100000 ,跳出。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<queue> 6 #include<algorithm> 7 using namespace std; 8 typedef long long ll; 9 void solve(){ 10 int t; 11 scanf("%d",&t); 12 while(t--){ 13 ll a,b,c,d; 14 cin>>a>>b>>c>>d; 15 int x1,x2,y1,y2; 16 ll ans = 0; 17 for(int i = 63; i>=0; i--){ 18 x1 = (bool)(a&((ll)1<<i)); 19 x2 = (bool)(b&((ll)1<<i)); 20 y1 = (bool)(c&((ll)1<<i)); 21 y2 = (bool)(d&((ll)1<<i)); 22 if(x1 == x2&&y1 == y2){ 23 if(x1 != y1){ 24 ans += ((ll)1<<i); 25 } 26 } 27 else if(x1 != x2&&y1 == y2){ 28 ans += ((ll)1<<i); 29 if(y1 == 1){ 30 b = ((ll)1<<i) - 1; 31 } 32 else{ 33 a = ((ll)1<<i); 34 } 35 } 36 else if(x1 == x2&&y1 != y2){ 37 ans += ((ll)1<<i); 38 if(x1 == 1){ 39 d = ((ll)1<<i) - 1; 40 } 41 else{ 42 c = ((ll)1<<i); 43 } 44 } 45 else if(x1 != x2&&y1 != y2){ 46 ans += ((ll)1<<(i+1))-1; 47 break; 48 } 49 } 50 cout<<ans<<endl; 51 } 52 } 53 int main() 54 { 55 solve(); 56 return 0; 57 }
