动态规划

动态规划

（参考灯神视频）

1.fibnacci(热身)

fibnacci问题如果我们直接递归求解，则花费时间复杂度为O(n^2)，但是我们只要进行保存状态，则可以转化为O(n)

// O(n^2)
int fibnacci_recrusion(int n) {
    if(n == 1 || n == 2) return 1;
    return fibnacci_recrusion(n - 1) + fibnacci_recrusion(n - 2);
}
// O(n)
int fibnacci_loop(int n) {
    int arr[99999];
    arr[1] = arr[2] = 1;
    for(int i = 3; i <= n; i++) 
        arr[i] = arr[i - 1] + arr[i - 2];
    return arr[n];
}

这就是重叠子问题

2.任务

每个任务占用以下时间片，每个任务可以赚红字的钱，我们如何利用dp进行求解

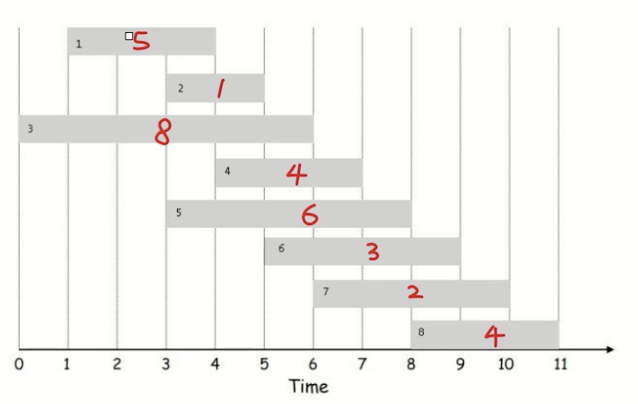
思路，我们对每个任务都有选和不选两种。然后进行递归求解，v代表

[Opt(i) = max(v(i) + opt(i - 1), v(i-1)) ]

我们还需要一个prev最优解

i           1  2  3  4  5  6  7  8  (选中)
prev(i)     0  0  0  1  0  2  3  5  (前面紧跟的)
opt(i)      5  5  8  9  9  9  10 13 

3.选数字

从4 1 1 9 1，选出不相邻的两个，并且和最大，我们也是同样的思路，找prev，和优化的数组，进行循环

#include <iostream>
using namespace std;
int arr[] = { 4, 1, 1, 9, 1 };
int _prev[] = { 0, 0, 1, 2, 3, 4 };
int optimize[5];
int main() {
    optimize[0] = optimize[1] = max(arr[0], arr[1]);
    for(int i = 2; i < sizeof(arr); i++)
        optimize[i] = max(optimize[i - 1], arr[i] + optimize[i - 2]);
    printf("%d", optimize[4]);
    return 0;
}

4.特定子列和

从3，34，4，12，2找找有无可能会有n个数相加和为9，如果有，则打印true

思考：我们选，前面的subset则要是减去这个数，否则是直接子列

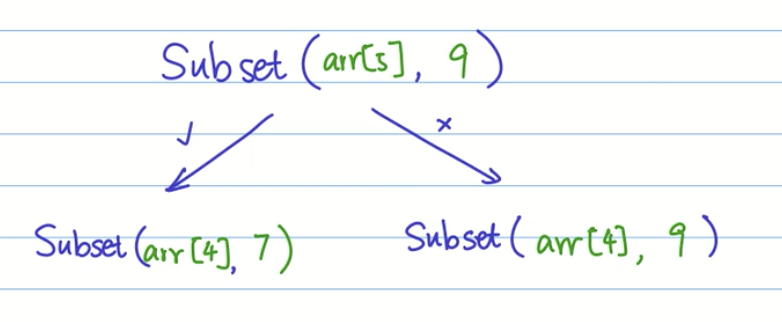
#include <iostream>
using namespace std;
int arr[] = { 3, 34, 4, 12, 2 };
bool subset(int i, int sum) {
    if(sum == 0) return true;
    else if(i == 0) return arr[0] == sum;
    else if(arr[i] > sum) return subset(i - 1, sum);
    else return subset(i - 1, sum - arr[i]) || subset(i - 1, sum);
}
int main() {
    printf("%d", subset(4, 4));
    return 0;
}
// 我们也可以转换成循环