树的总结（遍历，BST，AVL原型，堆，练习题）

树

@

目录

• 树
  • 一.抽象数据类型
  • 二、二叉树的性质
  • 三、二叉树的遍历
    • 3.1.递归
    • 3.2.非递归
    • 3.3.利用队列进行层序遍历
    • 3.4.已知先序中序求后序
    • 3.5.已知中序后序求先序
    • 3.6.先序构建树
  • 三、活用树的遍历
    • 3.1.PAT Advanced 1020 Tree Traversals
    • 3.2.PAT Advanced 1086 Tree Traversals Again 参考PAT官网原题
  • 四、BST树
    • 原型以及增删
  • 五、AVL树
    • 5.1.AVL树概念
    • 5.2.AVL树原型
    • 5.3.AVL树LL旋转
    • 5.4.AVL树LR旋转
    • 5.5.AVL树插入函数
  • 六、BST树和AVL树练习
    • 6.1.浙大习题7-4 是否是同一棵二叉搜索树
    • 6.2.PAT Advanced 1066 Root of AVL Tree (25 分) 参考PAT官网
  • 七、堆
    • 7.1.创建堆
    • 7.2.向下调整
    • 7.3.删除堆顶元素
    • 7.4.增加一个元素
    • 7.5.向上调整
    • 7.6.堆排序
    • 7.7.复用型heap.h文件
    • 7.8.测试文件

一.抽象数据类型

1.顺序存储

使用数组存储
父亲索引为 n
左孩子 2*n 右孩子 2*n+1

2.链式存储

typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
struct TNode{ /* 树结点定义 */
    ElementType Data; /* 结点数据 */
    BinTree Left;     /* 指向左子树 */
    BinTree Right;    /* 指向右子树 */
};

二、二叉树的性质

1.二叉树第i层最大结点数为：2^(i-1),i>=1

2.深度为k的二叉树最大结点总数为：2^k-1,k>=1

3.对任何非空二叉树T，若n0表示叶子结点个数、n2是度为2的非叶子结点个数，那么二者满足关系n0=n2+1

三、二叉树的遍历

3.1.递归

void PreOrderTraversal(BinTree BT){
	if(BT){
		printf("%d",BT->Data);
		PreOrderTraversal(BT->Left);
		PreOrderTraversal(BT->Right);
	}
}

中序后序同理，把打印放在中间和后面，这里不加以赘述。

3.2.非递归

以链式中序为例

void InOrderTraversal(BinTree BT){
	BinTree T=BT;
	Stack S=CreatSatck(MaxSize);
	while(T||!IsEmpty(S)){
		Push(S,T);
		T=T->Left;
	}
	if(!IsEmpty(S)){
		T=Pop(S);
		printf("%5d",T->Data);
		T=T->Right;
	}
}

3.3.利用队列进行层序遍历

void levelOrderTraversal(Tree *tr){
    queue<Tree*> que;
    Tree *t=tr;
    if(t==NULL) return;
    que.push(t);
    while(!que.empty()){
        t=que.front();
        que.pop();
        printf("%d
",t->val);
        if(t->left!=NULL) que.push(t->left);
        if(t->right!=NULL) que.push(t->right);
    }
}

3.4.已知先序中序求后序

#include <cstdio>
using namespace std;
int post[] = {3, 4, 2, 6, 5, 1};
int in[] = {3, 2, 4, 1, 6, 5};
void pre(int root, int start, int end) {
    if(start > end) return ;
    int i = start;
    while(i < end && in[i] != post[root]) i++;
    printf("%d ", post[root]);
    pre(root - 1 - end + i, start, i - 1);
    pre(root - 1, i + 1, end);
}
 
int main() {
    pre(5, 0, 5);
    return 0;
}

3.5.已知中序后序求先序

#include <cstdio>
using namespace std;
int pre[] = {1, 2, 3, 4, 5, 6};
int in[] = {3, 2, 4, 1, 6, 5};
void post(int root, int start, int end) {
    if(start > end) 
        return ;
    int i = start;
    while(i < end && in[i] != pre[root]) i++;
    post(root + 1, start, i - 1);
    post(root + 1 + i - start, i + 1, end);
    printf("%d ", pre[root]);
}

int main() {
    post(0, 0, 5);
    return 0;
}

3.6.先序构建树

TreeNode* buildTree(int root, int start, int end) {
    if(start > end) return NULL;
    int i = start;
    while(i < end && in[i] != pre[root]) i++;
    TreeNode* t = new TreeNode();
    t->left = buildTree(root + 1, start, i - 1);
    t->right = buildTree(root + 1 + i - start, i + 1, end);
    t->data = pre[root];
    return t;
}

三、活用树的遍历

3.1.PAT Advanced 1020 Tree Traversals

参考 https://pintia.cn/problem-sets/994805342720868352/problems/994805485033603072

这是一道考察树的构成，后序中序转前序，前序构造树，树层序遍历的一道题目，知识点考察很多

原题翻译：
已知后序遍历，中序遍历，求层序遍历
输入：一共有多少值
第一行为后序遍历，第二行为中序遍历
输出：层序遍历

Sample Input:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
Sample Output:
4 1 6 3 5 7 2

根据二中的方法，我们可以进行活用

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

struct TreeNode{//树的抽象类型
    int val;
    TreeNode *left;
    TreeNode *right;
};

vector<int> pre,in,post,ans;
queue<TreeNode*> que;

void preOrder(int root,int start,int end){//由中序后序建立前序
    if(start>end) return;
    int i=0;
    while(i<=end&&in[i]!=post[root]) i++;
    pre.push_back(post[root]);
    preOrder(root-1-end+i,start,i-1);
    preOrder(root-1,i+1,end);
}

TreeNode* buildTree(int root,int start,int end){//由前序中序构建树
    if(start>end) return NULL;
    int i=0;
    TreeNode *t=new TreeNode();
    while(i<=end&&in[i]!=pre[root]) i++;
    t->val=pre[root];
    t->left=buildTree(root+1,start,i-1);
    t->right=buildTree(root+1+i-start,i+1,end);
    return t;
}

void levelOrder(TreeNode *tree){//层序遍历树
    que.push(tree);
    while(!que.empty()){
        TreeNode *tmp=que.front();
        ans.push_back(tmp->val);
        que.pop();
        if(tmp->left!=NULL) que.push(tmp->left);
        if(tmp->right!=NULL) que.push(tmp->right);
    }

}
int main()
{
    int N;
    scanf("%d",&N);
    post.resize(N);in.resize(N);
    for(int i=0;i<N;i++) scanf("%d",&post[i]);
    for(int i=0;i<N;i++) scanf("%d",&in[i]);
    preOrder(N-1,0,N-1);
    TreeNode *tree=buildTree(0,0,N-1);
    levelOrder(tree);
    for(int i=0;i<ans.size();i++)
        if(i!=ans.size()-1) cout<<ans[i]<<" ";
        else cout<<ans[i];
    system("pause");
    return 0;
}

查看柳婼大神的博客，我们可以知道，有更简单的方法，仅仅加一个索引值，便可以达到相同的效果，代码如下：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
struct node{
    int index;
    int val;
};
bool cmp(node n1,node n2){
    return n1.index<n2.index;
}
vector<int> in,post;
vector<node> ans;

void preOrder(int root,int start,int end,int index){
    if(start>end) return;
    int i=0;
    while(i<=end&&in[i]!=post[root]) i++;
    ans.push_back({index,post[root]});
    preOrder(root-1-end+i,start,i-1,2*index+1);
    preOrder(root-1,i+1,end,2*index+2);
}
int main()
{
    int N;
    scanf("%d",&N);
    post.resize(N);in.resize(N);
    for(int i=0;i<N;i++) scanf("%d",&post[i]);
    for(int i=0;i<N;i++) scanf("%d",&in[i]);
    preOrder(N-1,0,N-1,0);
    sort(ans.begin(),ans.end(),cmp);
    for(int i=0;i<N;i++)
        if(i!=N-1) printf("%d ",ans[i].val);
        else printf("%d",ans[i].val);
    system("pause");
    return 0;
}

3.2.PAT Advanced 1086 Tree Traversals Again 参考PAT官网原题

这道题比上面一题简单，简单叙述

给先序遍历的进栈出栈过程，求后序遍历。
输入：数量 进栈出栈过程
输出：后序遍历

Sample Input:
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
Sample Output:
3 4 2 6 5 1

我们可以知道，先序遍历的出栈就是中序遍历打印，于是代码如下：

#include <iostream>
#include <vector>
#include <stack>
#include <cstring>

using namespace std;

vector<int> pre,in,post,val;

void postorder(int root,int start,int end){//中序，后序找前序
    if(start>end) return ;
    int root_index=0;
    while(root_index<=end&&in[root_index]!=pre[root]) root_index++;
    postorder(root+1,start,root_index-1);
    postorder(root+1+root_index-start,root_index+1,end);
    post.push_back(pre[root]);
}
int main()
{
    stack<int> sta;
    int k=0,N;
    char ch[5];int num;
    scanf("%d",&N);
    while(~scanf("%s",&ch)){
        if(strlen(ch)==4) {
            scanf("%d",&num);
            pre.push_back(num);
            sta.push(num);
        }else{
            in.push_back(sta.top());
            sta.pop();
            //if(in.size()==N) break;//测试代码的时候，可以把这句加上，因为官方使用的是文件测，所以支持~scanf的写法
        }
    }
    postorder(0,0,N-1);
    for(int i=0;i<N;i++)
        if(i!=N-1) printf("%d ",post[i]);
        else printf("%d",post[i]);

    system("pause");
    return 0;
}

四、BST树

原型以及增删

C语言BST树原型，BST树在进行增删的时候效率没有链表高，但是在查找的时候比较快，这边以BST原型，用C程序构造一个BST树。

#ifndef BSTTREE_H_INCLUDED
#define BSTTREE_H_INCLUDED

#define ElementType int
#define Position BSTTree*


typedef struct BSTTree{
    ElementType Data;
    struct BSTTree *Left;
    struct BSTTree *Right;
}BSTTree;



Position FindMin(BSTTree *bstTree){//递归查找
    if(!bstTree) return NULL;
    else if(!bstTree->Left) return bstTree;
    else return FindMin(bstTree->Left);
}

Position FindMax(BSTTree *bstTree){//循环查找
    if(bstTree)
        while(bstTree->Right) bstTree=bstTree->Right;
    return bstTree;
}

BSTTree* Insert(ElementType x,BSTTree *bstTree){
    if(bstTree){
        bstTree=malloc(sizeof(struct BSTTree));
        bstTree->Data=x;
        bstTree->Left=NULL;
        bstTree->Right=NULL;
    }else{
        if(x<bstTree->Data) bstTree->Left=Insert(x,bstTree->Left);
        else if(x>bstTree->Data) bstTree->Right=Insert(x,bstTree->Right);
        //else 啥也不做
    }
    return bstTree;
}

BSTTree* Delete(ElementType x,BSTTree *bstTree){
    Position Tmp;
    if(!bstTree) printf("not find");
    else if(x<bstTree->Data) bstTree->Left=Delete(x,bstTree->Left);//左递归删除
    else if(x>bstTree->Data) bstTree->Right=Delete(x,bstTree->Right);//右递归删除
    else
        if(bstTree->Left&&bstTree->Right){//左右两个孩子
            Tmp=FindMin(bstTree->Right);//右子树找最小元素填充删除节点
            bstTree->Data=Tmp->Data;
            bstTree->Right=Delete(bstTree->Data,bstTree->Right);//继续删除右子树最小元素
        }else{//有一个孩子或者没有孩子
            Tmp=bstTree;
            if(!bstTree->Left)
                bstTree=bstTree->Right;//直接赋值有孩子
            else if(!bstTree->Left)
                bstTree=bstTree->Left;//直接赋值左孩子
            free(Tmp);//进行释放
        }
    return bstTree;
}
#endif // BSTTREE_H_INCLUDED

五、AVL树

5.1.AVL树概念

什么是AVL树，比BST树多了一个平衡因子（Balance Factor），简称BF：BF(T)=hl-hr,其中hl和hr为左右子树的高度。

当平衡因子大于1的时候，我们就可以进行旋转操作

1.RR旋转（右单旋）

2.LL旋转（左单旋）

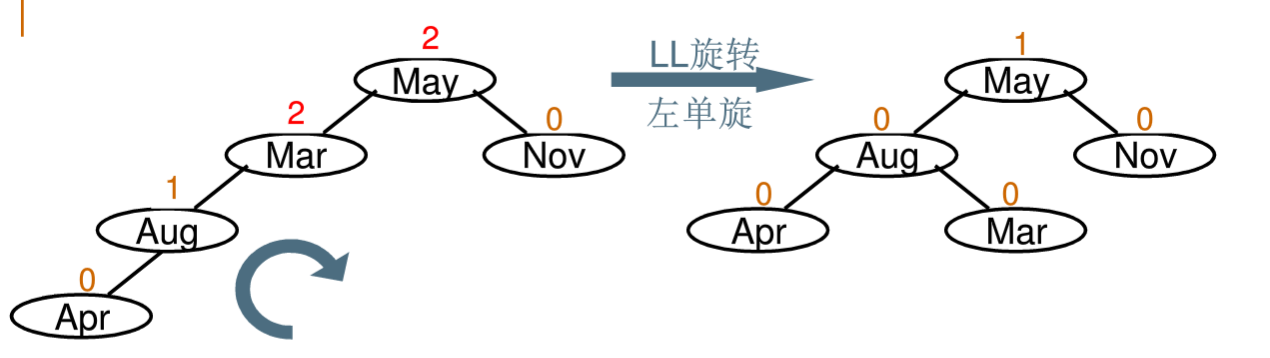
3.LR旋转（左右双旋）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-46YFPG97-1571396745491)(C:Users74302AppDataRoamingTypora ypora-user-images1571053306116.png)]

5.2.AVL树原型

#define ElementType int
typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode{
    ElementType Data; /* 结点数据 */
    AVLTree Left;     /* 指向左子树 */
    AVLTree Right;    /* 指向右子树 */
    int Height;       /* 树高 */
};

5.3.AVL树LL旋转

AVLTree SingleLeftRotation(AVLTree A){
/* 注意：A必须有一个左子结点B */
/* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */
    AVLTree B = A->Left;
    A->Left = B->Right;
    B->Right = A;
    A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
    B->Height = Max( GetHeight(B->Left), A->Height ) + 1;

    return B;
}

5.4.AVL树LR旋转

AVLTree DoubleLeftRightRotation ( AVLTree A )
{ /* 注意：A必须有一个左子结点B，且B必须有一个右子结点C */
  /* 将A、B与C做两次单旋，返回新的根结点C */

    /* 将B与C做右单旋，C被返回 */
    A->Left=SingleRightRotation(A->Left);
    /* 将A与C做左单旋，C被返回 */
    return SingleLeftRotation(A);
}

5.5.AVL树插入函数

AVLTree Insert( AVLTree T, ElementType X )
{ /* 将X插入AVL树T中，并且返回调整后的AVL树 */
    if ( !T ) { /* 若插入空树，则新建包含一个结点的树 */
        T = (AVLTree)malloc(sizeof(struct AVLNode));
        T->Data = X;
        T->Height = 0;
        T->Left = T->Right = NULL;
    } /* if (插入空树) 结束 */

    else if ( X < T->Data ) {
        /* 插入T的左子树 */
        T->Left = Insert( T->Left, X);
        /* 如果需要左旋 */
        if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
            if ( X < T->Left->Data )
               T = SingleLeftRotation(T);      /* 左单旋 */
            else
               T = DoubleLeftRightRotation(T); /* 左-右双旋 */
    } /* else if (插入左子树) 结束 */

    else if ( X > T->Data ) {
        /* 插入T的右子树 */
        T->Right = Insert( T->Right, X );
        /* 如果需要右旋 */
        if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
            if ( X > T->Right->Data )
               T = SingleRightRotation(T);     /* 右单旋 */
            else
               T = DoubleRightLeftRotation(T); /* 右-左双旋 */
    } /* else if (插入右子树) 结束 */

    /* else X == T->Data，无须插入 */

    /* 别忘了更新树高 */
    T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;

    return T;
}

六、BST树和AVL树练习

6.1.浙大习题7-4 是否是同一棵二叉搜索树

给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

输入格式:

输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L，分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数，作为初始插入序列。最后L行，每行给出N个插入的元素，属于L个需要检查的序列。

简单起见，我们保证每个插入序列都是1到N的一个排列。当读到N为0时，标志输入结束，这组数据不要处理。

输出格式:

对每一组需要检查的序列，如果其生成的二叉搜索树跟对应的初始序列生成的一样，输出“Yes”，否则输出“No”。

输入样例:

4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0

输出样例:

Yes
No
No

这道题，仅仅需要进行构造一棵BST树，然后进行判断先序遍历的打印即可，AC代码如下。

#include <iostream>

using namespace std;

string traver_ini,traver_cmp;

struct BST{
    int val;
    BST *left;
    BST *right;
};
BST *ini,*cmp;
BST* BST_insert(BST *b,int val){
    if(b==NULL) {
        b=new BST();
        b->val=val;
        return b;
    }
    if(val<b->val) b->left=BST_insert(b->left,val);
    else if(val>b->val) b->right=BST_insert(b->right,val);
    return b;
}
void pre(BST *b,string& str){
    if(b==NULL) return;
    str+=(b->val+'0');
    pre(b->left,str);
    pre(b->right,str);
}
int main()
{
    int M,N,tmp;
    while(1){
        scanf("%d",&M);
        if(M==0) break;
        scanf("%d
",&N);
        ini=NULL;
        for(int i=0;i<M;i++){
            scanf("%d",&tmp);
            ini=BST_insert(ini,tmp);
        }
        traver_ini="";
        pre(ini,traver_ini);
        while(N--){
            cmp=NULL;
            for(int i=0;i<M;i++){
                scanf("%d",&tmp);
                cmp=BST_insert(cmp,tmp);
            }
            traver_cmp="";
            pre(cmp,traver_cmp);
            if(traver_cmp==traver_ini) printf("Yes
");
            else printf("No
");
        }
    }
    return 0;
}

6.2.PAT Advanced 1066 Root of AVL Tree (25 分) 参考PAT官网

简单叙述：
给定插入元素个数n
插入n个元素后，输出根节点元素值
Sample Input 1:
5
88 70 61 96 120
Sample Output 1:
70
Sample Input 2:
7
88 70 61 96 120 90 65
Sample Output 2:
88

解题方法，构造一棵AVL树，然后插入，求根即可

#include <iostream>

using namespace std;

struct node{//AVL节点原型
    int val;
    node *left,*right;
};
node *rotateRight(node *root){//右多，进行RR旋转
    node *t=root->right;
    root->right=t->left;
    t->left=root;
    return t;
}
node *rotateLeft(node *root){//左多，进行LL旋转
    node *t=root->left;
    root->left=t->right;
    t->right=root;
    return t;
}
node *rotateLeftRight(node *root){//左多，进行LR旋转
    root->left=rotateRight(root->left);
    return rotateLeft(root);
}
node *rotateRightLeft(node *root){//右多，进行RL旋转
    root->right=rotateLeft(root->right);
    return rotateRight(root);
}
int getHeight(node *root){//获得高度
    if(root==NULL) return 0;
    return max(getHeight(root->left),getHeight(root->right))+1;
}
node *insert(node *root,int val){
    if(root==NULL){//空的时候
        root=new node();
        root->val=val;
        root->left=root->right=NULL;
    }else if(val<root->val){//插左边
        root->left=insert(root->left,val);
        if(getHeight(root->left)-getHeight(root->right)==2)
            root=val<root->left->val?rotateLeft(root):rotateLeftRight(root);
            //如果比左还要小，只需要进行LL旋转，否则需要LR旋转
    }else{//插右边
        root->right=insert(root->right,val);
        if(getHeight(root->right)-getHeight(root->left)==2)
            root=val>root->right->val?rotateRight(root):rotateRightLeft(root);
            //如果比右还要打，只需进行RR旋转，否则需要RL旋转
    }
    return root;
}
int main()
{
    int n,tmp;cin>>n;
    node* root=NULL;
    for(int i=0;i<n;i++){
        cin>>tmp;
        root=insert(root,tmp);
    }
    cout<<root->val;
    system("pause");
    return 0;
}

七、堆

7.1.创建堆

void createHeap(){
    for(int i=n/2;i>=1;i--)
        downAjust(i,n);
}

7.2.向下调整

思想是，low代表孩子，high代表极限。我们在[low,high]范围进行调整，low和low+1为2*low的孩子。如果没有交换，那就break掉，交换了还要和上面父亲去比较。

void downAdjust(int low,int high){
    int i=low,j=i*2;//i为要调整的节点，j为左孩子
    while(j<=high){
        if(j+1<=high && heap[j+1]>heap[j]) j=j+1;
        if(heap[j]>heap[i]){
            swap(heap[j],heap[i]);
            i=j;j=i*2;
        }else break;
    }
}

7.3.删除堆顶元素

void deleteTop(){
    heap[1]=heap[n--];//用第n个数进行覆盖
    downAdjust(1,n);//之后进行向下调整第一个数
}

7.4.增加一个元素

void insert(int x){
    heap[++n]=x;
    upAdjust(1,n);
}

7.5.向上调整

void upAdjust(int low,int high){
    int i=high,j=i/2;
    while(j>=low){
        if(heap[j]<heap[i]){
            swap(heap[j],heap[i]);
            i=j;j=i/2;
        }else break;
    }
}

7.6.堆排序

void heapSort(){
    createHeap();
    for(int i=n;i>=2;i--){
        swap(heap[i],heap[1]);
        downAdjust(1,i-1);
    }
}

7.7.复用型heap.h文件

#ifndef HEAP_H_INCLUDED
#define HEAP_H_INCLUDED

#define maxn 1000

using namespace std;//这里面有swap函数

int heap[maxn];

void upAdjust(int low,int high){
    int i=high,j=i/2;
    while(j>=low){
        if(heap[j]<heap[i]){
            swap(heap[j],heap[i]);
            i=j;j=i/2;
        }else break;
    }
}

void downAdjust(int low,int high){
    int i=low,j=i*2;//i为要调整的节点，j为左孩子
    while(j<=high){
        if(j+1<=high && heap[j+1]>heap[j]) j=j+1;
        if(heap[j]>heap[i]){
            swap(heap[j],heap[i]);
            i=j;j=i*2;
        }else break;
    }
}

void createHeap(int n){
    for(int i=n/2;i>=1;i--)
        downAdjust(i,n);
}


void deleteTop(int n){
    heap[1]=heap[n--];//用第n个数进行覆盖
    downAdjust(1,n);//之后进行向下调整第一个数
}

void insert(int x,int n){
    heap[++n]=x;
    upAdjust(1,n);
}


void heapSort(int n){
    createHeap(n);
    for(int i=n;i>=2;i--){
        swap(heap[i],heap[1]);
        downAdjust(1,i-1);
    }
}
#endif // HEAP_H_INCLUDED

7.8.测试文件

#include <iostream>
#include "heap.h"
using namespace std;
int main(){
    extern int heap[maxn];
    extern int n;
    scanf("%d",&n);
    /**我们的堆序列是从[1,n]的*/
    for(int i=1;i<=n;i++) scanf("%d",&heap[i]);
    createHeap();//生成大根堆
    insert(4);//插入堆顶元素
    deleteTop();//删除堆顶
    heapSort();//排序
    for(int i=1;i<=n;i++) printf("%d%s",heap[i],i==n?"
":" ");
    system("pause");
    return 0;
}