AcWing 1319. 移棋子游戏

题目传送门

一、\(SG\) 函数

首先定义 \(mex\) 函数，这是施加于一个集合的函数，返回最小的不属于这个集合的非负整数

例：\(mex({1,2})=0,mex({0,1})=2,mex({0,1,2,4})=3\)

在一张有向无环图中，对于每个点 \(u\)，设其所有能到的点的 \(SG\) 函数值集合为集合 \(A\)，那么 \(u\) 的 \(SG\) 函数值为 \(mex(A)\)，记做 \(SG(u)=mex(A)\)
例图：

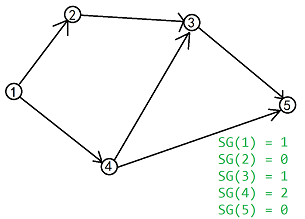
例图解释：
\(SG(5)=mex({∅})=0\)
\(SG(3)=mex({SG(5)})=mex({0})=1\)
\(SG(4)=mex({SG(5),SG(3)})=mex({0,1})=2\)
\(SG(2)=mex({SG(3)}=mex({1})=0\)
\(SG(1)=mex({SG(2),SG(4)})=mex({0,2})=1\)

---

二、本题思路

那么 \(SG\) 函数的定义说完了，这题和 \(SG\) 函数又有什么关系呢？
下面先说本题做法，再证明该方法正确性。

做法：求出每个棋子所在的点的 \(SG\) 函数值，将所有值异或起来。若异或值不为 \(0\)，则输出\(win\)，否则输出\(lose\)

证明：
首先，由于这是一张有向无环图，所以游戏最后一定会结束，也就是说每个棋子最后都会移动到一个点上，且该点没有任何能到达的点。

那么根据定义，结束状态的所有点的 \(SG\) 函数值异或起来为 \(0\)，做法对于结束状态可行。

所以接下来，只要证明出

• 证明I：任何一种每个棋子所在点的 \(SG\) 函数值异或起来非 \(0\) 的情况，一定能通过一次移动棋子，到达一个 每个棋子所在点的 \(SG\) 函数值异或起来为 \(0\) 的情况

• 证明II：任何一种每个棋子所在点的 \(SG\) 函数值异或起来为 \(0\) 的情况，一定不能通过一次移动棋子，到达一个每个棋子所在点的 \(SG\) 函数值异或起来为 \(0\) 的情况

那么做法就是对的

证明I：

设每个棋子所在点的 \(SG\) 函数值分别为 \(a_1,a_2,⋯,a_n\)

设 \(x=a_1 ∧ a_2 ∧ ⋯ ∧ a_n\)，设 \(x\) 的最高位为第 \(k\) 位，那么在 \(a_1,a_2,⋯,a_n\) 中，一定有一个值\(a_i\)的第 \(k\) 位为 \(1\)

由于 \(x\) 的第 \(k\) 位和 \(a_i\) 的第 \(k\) 位都是 \(1\)，且第 \(k\) 位是 \(x\) 的最高位，所以 \(a_i ∧ x\) 一定小于 \(a_i\)

又因为 \(a_i\) 是其中一个棋子所在点的 \(SG\) 函数值，那么根据 \(SG\) 函数值的定义，该点能到达的所有点中，一定存在一个点的 \(SG\) 函数值为 \(a_i ∧ x\)

那么我们就可以将该点上的棋子，移到一个 \(SG\) 函数值为 \(a_i ∧ x\) 的点上去

移完之后，原来每个棋子所在点的 \(SG\) 函数异或值就变为了

\(a_1 ∧ a_2 ∧ ⋯ ∧ a_{i−1} ∧ (a_i ∧ x) ∧ a_{i+1} ⋯ ∧ a_n =(a_1 ∧ a_2 ∧ ⋯ ∧ a_n) ∧ x=x ∧ x=0\)

证毕

证明II：

反证法:设将点 \(u\) 上的棋子移动到点 \(v\) 上后，每个棋子所在点的 \(SG\) 函数值仍然为 \(0\)
那就说明 \(SG(u)=SG(v)\)，不符合 \(SG\) 函数的定义，不成立

证毕

所以做法是正确的。

---

三、如何求出每个点的 \(SG\) 函数值

记忆化搜索就好啦~

每层记忆化搜索中，如果该点的 \(SG\) 函数值已经被计算出，那就直接返回该值。否则用一个 \(set\) 记录每个点能到的所有点的 \(SG\) 函数值集合，然后从 \(0\) 开始遍历，找到第一个 \(set\) 里面没有的数，将该值记录在该点上并返回。

四、时间复杂度

最坏情况下，每个点都会被遍历一次，时间复杂度为 \(O(n)\)。

对于每个点，我们会将其所能到达的所有点扔到一个 \(set\) 中。

而每个点能到达的点的数量，取决于从该点出发的边的数量。

所以总共我们会往 \(set\) 中插入 \(m\) 次。

但是对于每个 \(set\)，我们至多只会往其中插入 \(n - 1\) 个数。

所以对于 \(set\) 的总复杂度为 \(O(mlogn)\)。

那么本题的总时间复杂度即为 \(O(n+mlogn)\)。

五、实现代码

#include <bits/stdc++.h>

using namespace std;
const int N = 2010, M = 6010;

// SG函数模板题
int n, m, k;
int f[N];

int h[N], e[M], ne[M], idx;
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int sg(int u) {
    //记忆化搜索
    if (f[u] != -1) return f[u];

    //找出当前结点u的所有出边，看看哪个sg值没有使用过
    set<int> S;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        S.insert(sg(j));
    }

    //找到第一个没有出现的过的自然数， 0,1,2,3,4,...
    for (int i = 0;; i++)
        if (S.count(i) == 0) {
            f[u] = i;
            break;
        }

    return f[u];
}

int main() {
    memset(h, -1, sizeof h); //初始化邻接表

    scanf("%d%d%d", &n, &m, &k);
    while (m--) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }

    memset(f, -1, sizeof f); //初始化sg函数的结果表
    int res = 0;
    for (int i = 0; i < k; i++) {
        int u;
        scanf("%d", &u);
        res ^= sg(u); //计算每个出发点的sg(u)，然后异或在一起
    }

    if (res) //所有出发点的异或和不等于0,先手必胜
        puts("win");
    else //所有出发点的异或和等于0，先手必败
        puts("lose");

    return 0;
}