AcWing 1315. 网格

题目传送门

• 用求卡特兰数的方法分析一下这个题目就可以得到答案，关于卡特兰数的分析：网址

• 我们需要求出点(\(n, m\))关于\(y = x + 1\)对称的点的坐标，假设为\((a, b)\)，则任何一种不合法的方案都可以转化为到达\((a, b)\)的路径，如下图：

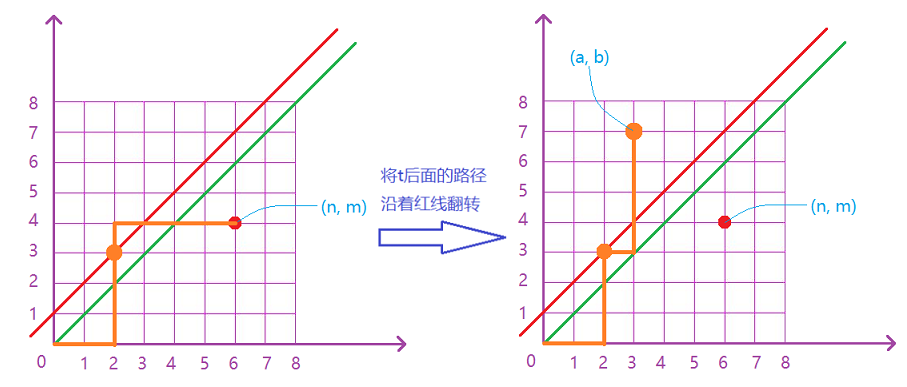
则答案为：\(\large \displaystyle C_{m+n}^n-C_{m+n}^a\)，问题就转变为了如何求解坐标\((a, b)\)

这种对称，\(yxc\)大佬给出的方法是：平移对称轴

• 将直线\(y=x+1\)、点\((n,m)\)全部向下移动一个单位，就变成了一条直线\(y=x\)和点\((n,m-1)\)
• 求\((n,m-1)\)关于直线\(y=x\)的对称点就是\((m-1,n)\)
• 再将直线和点全部上移回去，就得到\((m-1,n+1)\)

因此，答案： \(\LARGE \displaystyle C_{m+n}^n-C_{m+n}^{m-1}\)

本题需要使用到高精度求解，如果递推的话计算量为\(10000^2=1×10^8\)，再加上高精度计算会超时，因此这里求解阶乘的方式然后带入公式求组合数，类似于AcWing 888. 求组合数 IV。

#include <bits/stdc++.h>

using namespace std;

//运行时间：78 ms
const int N = 100010;
int a[N], b[N]; //两个整数数组保存高精度计算的结果

//问题1：本题是用静态数组计算的高精度，而不是用的基础课中教的vector办法，性能更好。但问题是，这样还可以压位吗？
//问题2：既然可以用静态数组来计算卡特兰数+高精度，那么，基础课的那道01序列的题，是不是也应该可以使用静态数组+高精度来实现？

//欧拉筛
int primes[N], cnt;
bool st[N];
void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

//计算n！中包含质数p的个数
int get(int n, int p) {
    int s = 0;
    while (n) s += n / p, n /= p;
    return s;
}

//高精度乘低精度
void mul(int a[], int b, int &len) {
    int t = 0;
    for (int i = 1; i <= len; i++) {
        t += a[i] * b;
        a[i] = t % 10;
        t /= 10;
    }
    while (t) {
        a[++len] = t % 10;
        t /= 10;
    }
}

//高精减高精
void sub(int a[], int b[], int &len) {
    for (int i = 1, t = 0; i <= len; i++) {
        a[i] -= t + b[i];
        if (a[i] < 0)
            a[i] += 10, t = 1;
        else
            t = 0;
    }
    while (len > 1 && !a[len]) len--;
}

// C(a,b)的结果，高精度保存到c数组，同时，返回c数组的长度len
int C(int a, int b, int c[]) {
    //高精度的基底，乘法的基数是1
    c[1] = 1;
    int len = 1; //由于高精度数组中只有一位，是1，所以长度也是1

    for (int i = 0; i < cnt; i++) { //枚举区间内所有质数
        int p = primes[i];
        /*
        C(a,b)=a!/(b! * (a-b)!)
        a!中有多少个质数因子p
        减去(a-b)!的多少个质数因子p,
        再减去b!的质数因子p的个数，就是总个数
        s记录了p这个质数因子出现的次数
        */
        int s = get(a, p) - get(b, p) - get(a - b, p);
        while (s--) mul(c, p, len); // 不断的乘p,结果保存到数组c中。len将带回c的有效长度
    }
    return len; //返回结果数组c的数位长度
}

int main() {
    //加快读入
    ios::sync_with_stdio(false);

    //筛质数
    get_primes(N - 1);

    int n, m;
    cin >> n >> m;
    int al = C(n + m, m, a);     // C(n+m,m)，将高精度结果记录到a数组中,返回数组有效长度al
    int bl = C(n + m, n + 1, b); // C(n+m,n+1)，将高精度结果记录到b数组中

    sub(a, b, al); //计算a-b的高精度减法
    //输出结果，注意是倒序
    for (int i = al; i >= 1; i--) printf("%d", a[i]);
    return 0;
}