引理一
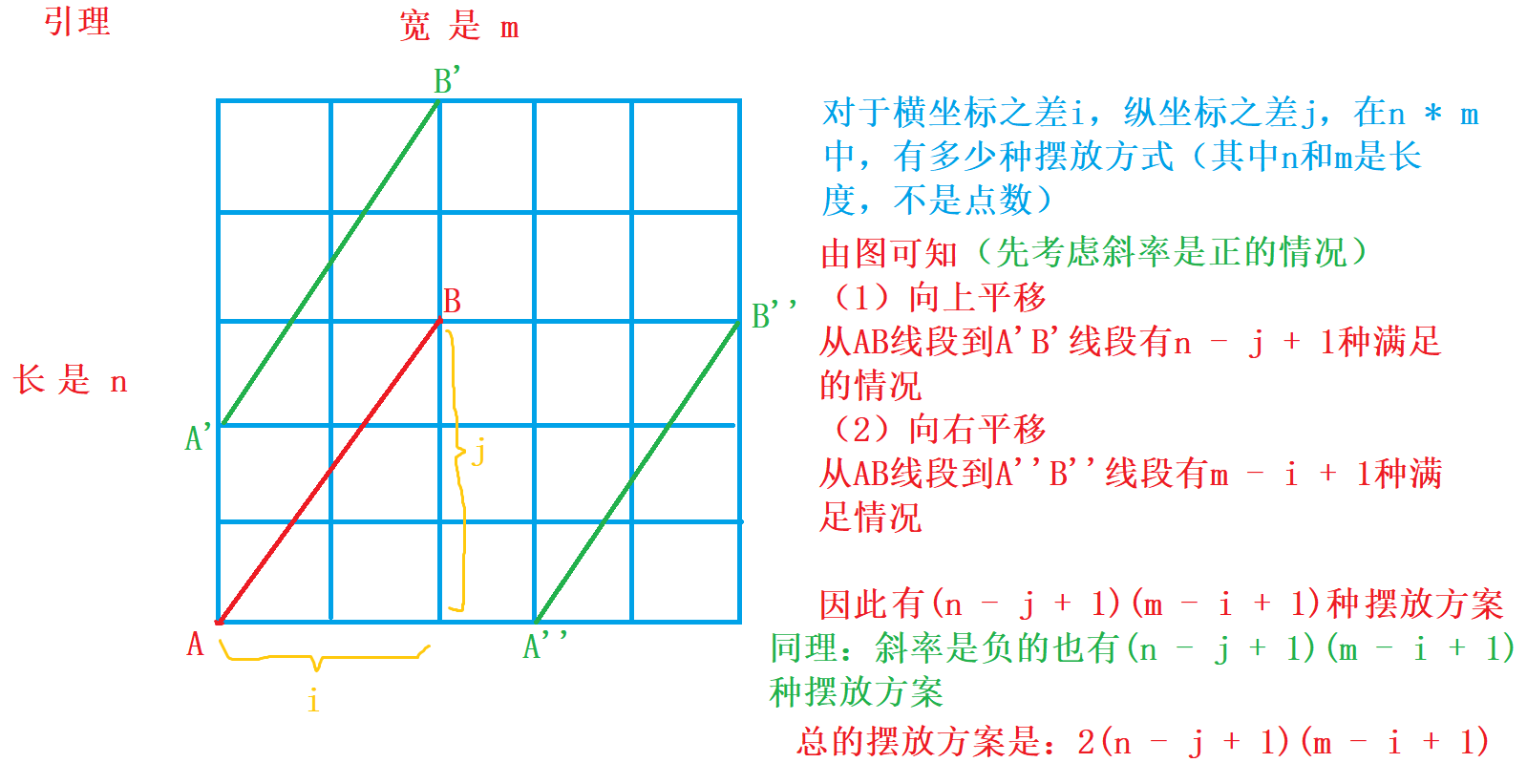
引理二
\(gcd(i,j)−1\)的证明
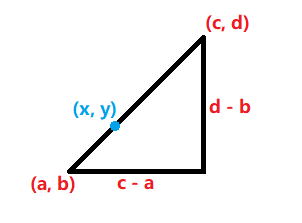
对于斜边上的任何一点 \((x,y)\), 其满足:
\[\large \frac{y-b}{x-a}=\frac{d-b}{c-a}
\]
注意:\(a≤x≤c,b≤y≤d\)
可知:$$\large \displaystyle y=\frac{d-b}{c-a}(x-a)+b=\frac{\frac{d-b}{gcd(d-b,c-a)}}{\frac{c-a}{gcd(d-b,c-a)}}(x-a)+b
\
\Rightarrow
\
y=\frac{d-b}{gcd(d-b,c-a)}*\frac{x-a}{\frac{c-a}{gcd(d-b,c-a)}}+b \ \ \ x \in Z^+
\[
那么如果使得 $y∈Z^+$ 的话,必须使得 $\large \displaystyle \frac{c-a}{gcd(d-b,c-a)}|(x-a)$,即:
$$\large x=\frac{c-a}{gcd(d-b,c-a)}*q+a\]
对于条件 \(b≤y≤d\) 上述式子是由直线方程推出的,因此其在方程中等价于 \(a≤x≤c\), 因此我们只需要考虑 \(x\) 的范围限制即可:
\[\large a≤x=\frac{c-n}{gcd(d-b,c-a)}*q+a≤c
\\
\Rightarrow
0 ≤ q ≤ gcd(d-b,c-a)
\]
\(q\) 可以取这个区间中的所有整数,因此数量为 \(gcd(d−b,c−a)+1\)
然后我们分析对于区间中的任意一个点 \((x,y)\), 由于上面 \(q\) 的范围可知 \(a≤x≤c\), 因此均在斜边上不加上两个端点的话,就是 \(gcd(d−b,c−a)−1\)
算法分析
本题使用 容斥原理 的思想
题目给定长是\(n\),宽是\(m\)的矩形,因此总端点数有\((n + 1) * (m + 1)\)个,从总端点数选\(3\)个点的情况有
\(\large \displaystyle C_{(n+1)∗(m+1)}^3\)种,再将不符合三角形规则的情况减去即可,即 三角形的数目 = \(\large \displaystyle C_{(n+1)∗(m+1)}^3\)- 不满足要求的情况(三点共线)
不满足的情况
- 1、 斜率不存在:\((m+1)C_{n+1}^3\)
- 2、 斜率为\(0\):\((n+1)C_{m+1}^3\)
- 3、斜率存在且不为 \(0\):由两个端点 \(A,B\) 组成的横坐标之差是 \(i\) ,纵坐标之差是 \(j\) 的线段共有 \(2(n−j+1)(m−i+1)\) 条,对于每一条线段斜率上共有 \(gcd(i,j)+1\) 个端点,减去 \(A,B\) 两个端点,即第三个点有 \(gcd(i,j)−1\) 种满足情况,因此总方案数是 \(2(gcd(i,j)−1)(n−j+1)(m−i+1)\)