一、二次筛法
这里的区间范围给定的最大值是\(2^{31} - 1\),而用线性筛法求的是\([1,n]\)中的所有质数,因此直接用线性筛法求肯定会直接\(gg\),因此需要通过挖掘某些性质,才能有技巧性的完成。
二、挖掘性质
-
性质\(1\):
若一个数\(n\)是一个合数,必然存在\(2\)个因子\(d\),\(\frac{n}{d}\),假设\(d <=\frac{n}{d}\),则\(d <= \sqrt{n}\),因此必然存在一个小于等于 \(\sqrt{n}\)的因子 -
性质2
若\(x∈[L,R]\),且\(x\)是合数,则一定存在\(P <= \sqrt{2^{31}-1} (< 50000)\),使得\(P\)能整除\(x\),其中\(P < x\)。
\(\sqrt{2147483647}=46340\),这个值是小于\(50000\)的,所以,\(yxc\)一般喜欢使用直接写上上限值\(50000\),就是因为这个数字够用,而且够大,好记。
三、实现步骤
- 找出\(1 \sim \sqrt{2^{31}-1}\) \((< 50000)\)中的所有质因子
- 对于\(1 \sim 50000\) 中每个质数\(P\),将\([L,R]\)中所有\(P\)的倍数筛掉(至少\(2\)倍,\(1\)倍的就是自己,是质数不是合数)
找到大于等于\(L\)的最小的\(P\)的倍数\(P_0\),找下一个倍数时只需要\(+= P\)即可
四、引理
在寻找大于\(L\)的第一个\(P\)的倍数时,采用了下面的引理:
引理(分数的上取整转换下取整)
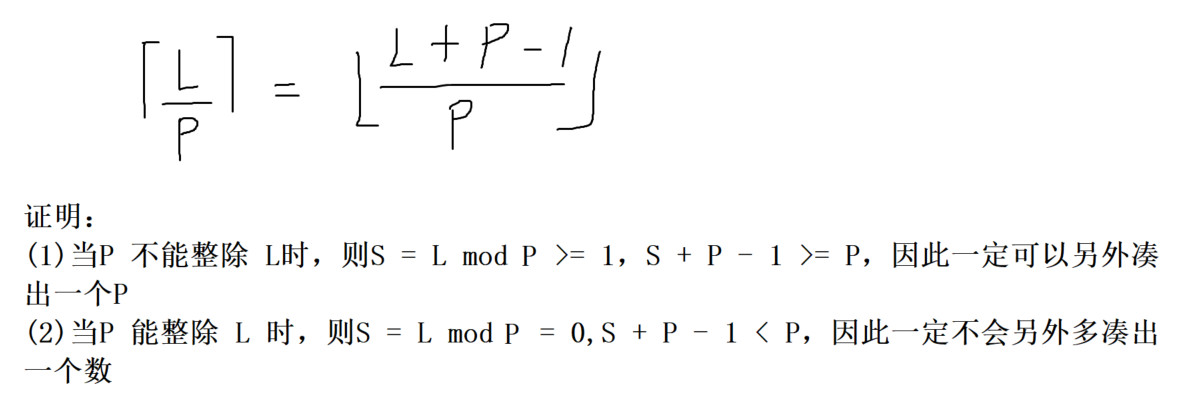
五、细节
\(Q\): 每个质数是\(2\sim 50000\)中的数,为啥 LL p = primes[i]; 这里的p的LL啊, int 不就够了吗?
\(A\): LL p = primes[i],这里p用LL是因为如果p也是用int类型,本身l也是用int类型,如果l取得足够大,下面的l + p - 1会有可能直接爆int 变成负数
\(Q\): for (LL j = max(p * 2, (l + p - 1) / p * p); j <= r; j += p) 这里的 j 是小于等于 r 的,而 r 的取值范围是小于\(2 ^ {31}\),也是在int 范围内啊, 这里为啥用LL啊?
\(A\): 这里的 j 是小于等于 r 的,而 r 的取值范围是小于\(2 ^ {31}\),这里确实是这样,可是这个循环跳出的条件是j <= r,也就是说如果r是最大的int,那么当j += p,要超过最大的int的时候需要比它还大才能跳出循环,因此直接爆int变成负数,然后j <= r依然成立,会一直死循环下去。其实本质上这个问题与问题\(1\)是一回事,在做数论时一次要小心\(LL\)和\(int\)的加法、乘法,小心爆\(int\)是一条死规则,尽量多想想是不是应该用\(LL\)来设置变量~
\(Q\): 我知道这里是复用st数组,但是在用之前都初始化为\(0\)了啊,为什么init(50000); 放在while (cin >> l >> r) 的外面(也就是最前面)代码不行啊?
\(A\):放在最前面也是可以的,\(y\)总的代码中判断从\([1,50000]\)中谁是质数和在区间\([L,R]\)中谁是质数直接复用\(st[]\)数组,就不用再开一个数组去存了,也可以把init()放在前面,用一个专门的数组去记录区间\([L,R]\)中谁是质数
\(Q\): 为什么要写上常数\(50000\)呢?
\(A\):
- 写法\(1\):
get_primes(50000) - 写法\(2\):
get_primes(sqrt(r)) - 写法\(3\):
get_primes(sqrt(INT32_MAX))
其实都行,但有了经验后,发现,直接写\(50000\)最简单粗暴效果好~
\(Q\): 为什么要使用偏移量st[j - l] = true?
\(A\): 因为数据范围太大,直接用数组进行桶计数,会超空间,需要离散化一下,就是把\(1e6\)范围内的数据映射到\(0\sim 1e6\)
\(Q\):为什么for (int i = 0; i < cnt - 1; i++) 这里要用cnt-1呢?为什么不是cnt呢?
\(A\):\(cnt\)个质数,下标是\([0,cnt-1]\),因为现在枚举的是前一个质数,要保证还有后一个,所以取不到\(cnt-1\)
\(Q\):实测\(STL\)中的\(unordered\_map\)用来替换\(st\)数组做桶,\(TLE\)!看来以后用桶尽量用数组模拟,如果范围大,就用偏移量才是王道!
六、时间复杂度
\(O(n)\)
七、实现代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
//欧拉筛
const int N = 1e6 + 10;
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n) {
memset(st, 0, sizeof st);
cnt = 0;
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] * i <= n; j++) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int main() {
int l, r; //起始值,终止值
while (~scanf("%d%d", &l, &r)) { //注意,这里在while循环中使有scanf,必须要使用~
get_primes(50000);
memset(st, 0, sizeof st); //给st数组以新的定义,用于判断[l,r]之间某个数字是不是可以被枚举的小质数因子筛掉
for (int i = 0; i < cnt; i++) { //枚举筛出的所有小质数因子
LL p = primes[i];
//将[l,r]之内,找出P的第一个整数倍(>=2)的数字,
for (LL j = max(p * 2, (l + p - 1) / p * p); j <= r; j += p)
st[j - l] = true; //防止数组越界,采用了一个偏移l的办法,可以理解为离散化
}
cnt = 0; //清空了primes数组,废物利用啊
for (int i = 0; i <= r - l; i++) //这里也使用了偏移l的办法
if (!st[i] && i + l >= 2) //如果i+l没有被筛掉,表示是质数,并且>=2,表示是真的质数
primes[cnt++] = i + l; //将数字i+l记录到质数数组中
if (cnt < 2)
puts("There are no adjacent primes."); //如果质数数量不足2个
else {
int minp = 0, maxp = 0;
// cnt个质数,下标是[0,cnt-1],因为现在枚举的是前一个质数,要保证还有后一个,所以取不到cnt-1
for (int i = 0; i < cnt - 1; i++) {
int d = primes[i + 1] - primes[i]; //计算相邻两个质数的差值
if (d < primes[minp + 1] - primes[minp]) minp = i; //对比记录最小质数差位置
if (d > primes[maxp + 1] - primes[maxp]) maxp = i; //对比记录最大质数差位置
}
printf("%d,%d are closest, %d,%d are most distant.\n",
primes[minp], primes[minp + 1],
primes[maxp], primes[maxp + 1]);
}
}
return 0;
}
八、桶的性能分析
上文中,采用了静态数组+偏移量的办法来模拟范围在\(1e6\)之间的数据情况,类似于桶排的思路。其实,\(STL\)中的\(unordered_map\)也可以实现相同的功能,而且不用考虑偏移问题,不是更好吗?实际情况是\(unordered_map\)在性能上和内存使用上都远不如静态数组!!在性能上大约慢35倍左右!!!!以后在算法竞赛中,应该忘记\(STL\)中的这个东东,不是\(TLE\)就是\(MLE\),要学会使用用数组模拟的思想和常用办法(离散化、偏移量等)
下面的是测试的情况:
#include <unordered_map>
#include <sys/time.h>
#include <iostream>
using namespace std;
const int N = 1010;
unordered_map<int, int> _map;
int times = 10000;
/*
Use unordered_map:time = 0.611364
Use static array:time = 0.018988
约是35倍左右,性能相差太大,以后在C++的算法竞赛中,避免使用unordered_map,采用离散化(偏移量)后在静态数组应对!
*/
int a[N], b[N];
int main() {
for (int i = 0; i < N; ++i) {
_map[i] = i;
a[i] = i;
b[i] = (i * 11 + i * i) % N;
}
int sum = 0;
struct timeval t1, t2;
double timeuse;
gettimeofday(&t1, NULL);
for (int i = 0; i < times; ++i)
for (int j = 0; j < N; ++j)
sum += _map[j];
gettimeofday(&t2, NULL);
timeuse = (t2.tv_sec - t1.tv_sec) + (double)(t2.tv_usec - t1.tv_usec) / 1000000.0;
cout << "Use unordered_map:time = " << timeuse << endl;
sum = 0;
gettimeofday(&t1, NULL);
for (int i = 0; i < times; ++i)
for (int j = 0; j < N; ++j)
sum += a[j];
gettimeofday(&t2, NULL);
timeuse = (t2.tv_sec - t1.tv_sec) + (double)(t2.tv_usec - t1.tv_usec) / 1000000.0;
cout << "Use static array:time = " << timeuse << endl;
return 0;
}