AcWing 253. 普通平衡树

题目传送门

一、题目解析

平衡树，\(Treap\)
众所周知\(Treap = BST + heap\)

堆不多说了。

说说这个\(BST\)，就是说一个根节点\(p\)，左儿子一定小于他，右儿子大于它。

也就是\(BST\)的中序遍历是严格单调递增的。

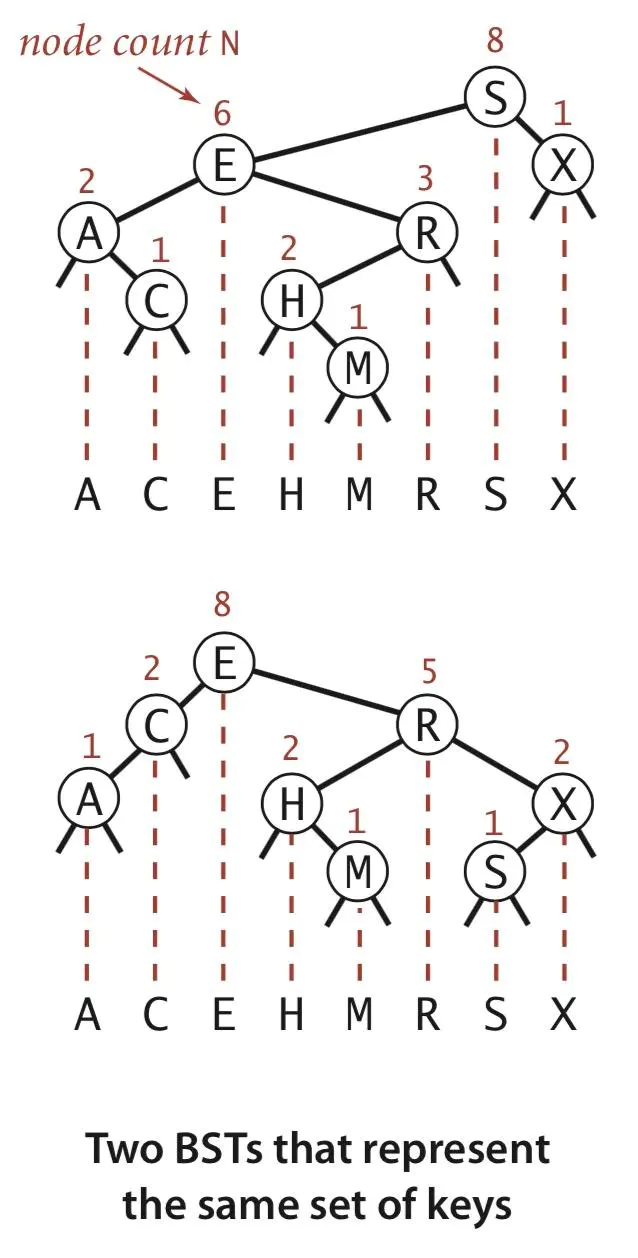
那么就可以进行一些操作了。

• 左旋与右旋

  首先为了维护这个\(BST\)我们需要一个左旋\(zag\)和右旋\(zig\)，分别表示将根节点和左右儿子交换位置，使交换后还满足\(BST\)的性质。

  这个相当于一个模拟了，代码放在后面。

• 插入

  这个可以从根节点开始，看看往左儿子走还是往右儿子走，一直走到空或者和自己相等的节点，然后进行插入。

• 删除
  从根节点走，走到了这个节点就删除掉，如果走到的节点为空，那就不用管了，因为这个节点不存在。

  还有就是删除的时候如果遇到了叶节点可以直接删除，不会影响\(BST\)的性质。

• 最大最小
  就是一直往左走或者一直往右走。

• 查排名和排名对应的数

  排名可以一点点走，然后分类讨论，这个可以看代码注释。

  排名对应的数也是一样，但这个得判断一下个数，所以\(BST\)里要有\(cnt\)和\(size\)两个变量表示节点个数和当前这个节点有多少个。

• 前驱和后继
  具体定义参见题目描述。

  方法也是一样，前驱就是左边最大的，后继就是右边最小的，可以用递归写，会简单很多。

  但是有的时候\(BST\)会退化成一条链，时间复杂度就大大升高了，但是只要\(BST\)够随机，期望高度就是\(log_2n\)。

  所以的话就把它和堆集合在了一起，变成了平衡树。

  其他的注释我放到代码里了。

二、实现代码

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
const int INF = 0x3f3f3f3f;
int n;
struct Node {
    int l, r; //左儿子右儿子的节点号
    int key;  //在BST中的数值
    int val;  //堆中的编号
    int cnt;  //当前节点是数字的个数
    int size; //以当前节点为根的子树中数字的总个数
} tr[N];
//比如tr[1] 就是1号节点，一般用来放根

int root, idx;

//上传节点信息，更新size
void pushup(int u) {
    //递归统计，左儿子数量+右儿子数量+自己本身节点上记录的数量
    tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + tr[u].cnt;
}

//创建新点,k为在BST中的数值
int newnode(int k) {
    tr[++idx].key = k;    //新开一个空间++idx,值k=k
    tr[idx].val = rand(); //尽量随机，随手给个就行
    tr[idx].cnt = tr[idx].size = 1; //叶子节点，所以此位置的数字个数为1，以它为根的子树中所有数字个数和也为1
    return idx;                     //返回节点号
}

void zig(int &u) //左右旋，没啥好说的，自己在纸上画一下就知道了
{
    int q = tr[u].l;
    tr[u].l = tr[q].r;
    tr[q].r = u;
    u = q;
    pushup(tr[u].r);
    pushup(u); //最后一定要记得上传，不然完了
}
void zag(int &u) {
    int q = tr[u].r;
    tr[u].r = tr[q].l;
    tr[q].l = u;
    u = q;
    pushup(tr[u].l);
    pushup(u);
}
//建树操作，为了正确性增加两个哨兵，防止越界
void build() {
    newnode(-INF), newnode(INF);          //初始化两个哨兵，一个值是-INF,一个值是INF，利用左右旋打开局面
    root = 1, tr[1].r = 2;                //初始化一下,根是1号结点，根的右儿子是2号节点
    pushup(root);                         //上传信息
    /*
        x               y
       / \  右旋zig    / \
      y   tt   ->     hh  x
     / \      <-         / \
    hh  z   左旋zag     z   tt
    */
    if (tr[1].val < tr[2].val) zag(root); //不平衡了就左旋一下,这两个点也要PK一下大小王，如上图，可理解为将右儿子变根
}
//在以u为根的子树中插入一个数字k,因为根可能在操作过程中左旋或右旋等变更根，所以u就以引用方式传入的
void insert(int &p, int key) {
    if (!p)
        p = newnode(key); //如果走到空了，就新建一个值为k的节点,并记录到u中，u似乎更像一个游标
    else {
        if (tr[p].key == key)
            tr[p].cnt++; //如果找到了相同的节点，就cnt++
        else {
            if (tr[p].key > key) {                       //看看是在左边还是在右边
                insert(tr[p].l, key);                    //准备向左边递归执行插入动作
                if (tr[tr[p].l].val > tr[p].val) zig(p); //插入完，不平衡立马调整，左侧插入右旋
            } else {
                insert(tr[p].r, key);                    //准备向右边递归执行插入动作
                if (tr[tr[p].r].val > tr[p].val) zag(p); //插入完，不平衡立马调整，右侧插入左旋
            }
        }
    }
    pushup(p); //最后上传一下，是不是和线段树有点像啊？
}

//删除操作
void del(int &p, int key) {
    if (p == 0) return;     //如果没了说明节点不存在，就不管了。
    if (tr[p].key == key) { //如果找到了这个点
        if (tr[p].cnt > 1)
            tr[p].cnt--;                           //大于一好说，直接cnt --
        else {                                     //不大于一
            if (tr[p].l || tr[p].r) {              //先看看是不是叶节点
                if (!tr[p].r || tr[tr[p].l].val) { //如果右儿子为空，或者 左侧随机值不为零
                    zig(p);                        //右旋
                    del(tr[p].r, key);             //在右边删除k
                } else {
                    zag(p);            //左旋
                    del(tr[p].l, key); //在左边删除k
                }
            } else
                p = 0; //直接删除
        }
    } else if (tr[p].key > key)
        del(tr[p].l, key); //在左侧删除
    else
        del(tr[p].r, key); //在右侧删除

    pushup(p); //上传更改
}

//获取k的排名,查询时，不需要修改游标u,不用按&地址符传递引用
int get_rank_by_key(int p, int key) {
    if (!p) return 0;                                                    //是0随便返回就行
    if (tr[p].key == key) return tr[tr[p].l].size + 1;                   //相等了那排名应该就是左边的数量加上自己
    if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);           //大了找左边
    return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key(tr[p].r, key); //找右边
}

//按rank排名查询值
int get_key_by_rank(int p, int rank) {
    if (!p) return INF;
    if (tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank);  //找左边
    if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;           //如果满足条件就直接return
    return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt); //不然就找右边
}

//前驱:找到严格小于key的最大数
int get_prev(int p, int key) {
    if (!p) return -INF;
    if (tr[p].key >= key) return get_prev(tr[p].l, key); //找左边
    return max(get_prev(tr[p].r, key), tr[p].key);       //可能是右边可能是这个数，所以用个max
}

//后继:找到严格大于key的最小数
int get_next(int p, int key) {
    if (!p) return INF; //后继的写法和前驱相反，大家可以注意一下
    if (tr[p].key <= key) return get_next(tr[p].r, key);
    return min(get_next(tr[p].l, key), tr[p].key);
}
int main() {
    build(); //建树，要是忘了就凉了
    scanf("%d", &n);
    while (n--) {
        int op, x;
        scanf("%d%d", &op, &x);

        if (op == 1) //插入一个数x
            insert(root, x);
        else if (op == 2) //删除一个数x
            del(root, x);
        else if (op == 3)
            printf("%d\n", get_rank_by_key(root, x) - 1); //获取数x的排名，因为有两个哨兵，一前一后，所以前面有1个
        else if (op == 4)
            printf("%d\n", get_key_by_rank(root, x + 1)); //按排名查值，因为有一个前置哨兵，在Treap中，实际的排名需要+1
        else if (op == 5)
            printf("%d\n", get_prev(root, x)); //获取x的前驱
        else
            printf("%d\n", get_next(root, x)); //获取x的后继
    }
    return 0;
}