\(AcWing\) \(372\). 棋盘覆盖
一、题目描述
给定一个 \(N\) 行 \(N\) 列的棋盘,已知某些格子禁止放置。
求最多能往棋盘上放多少块长度为 \(2\) 、宽度为 \(1\) 的骨牌,骨牌的边界与格线重合(骨牌占用 \(2\) 个格子),并且任意两张骨牌都不重叠。
二、二分图应用【匈牙利算法求最大匹配】
前置知识
-
匹配:二分图中两个点集中各取一点进行连边
-
最大匹配:二分图中左右两边匹配后边的最大数量
-
匹配点:属于其中一个匹配边的其中一个端点
-
增广路径:左边点集中的一个非匹配点,沿着非匹配边走到右边点集中的一个匹配点,再沿着匹配边走到左边点集中的一个匹配点,再沿着非匹配边走到右边点集中的一个匹配点 …… 最终走到右边点集中的一个非匹配点。
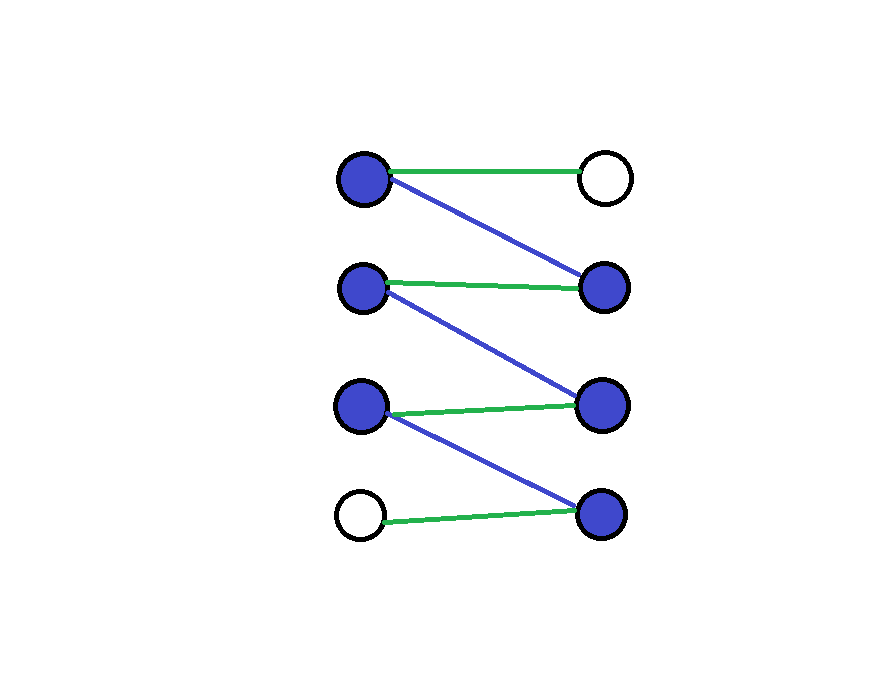
增广路径的起点和终点一定都是非匹配点,增广路径意味着我们可以将所有蓝色(匹配边)和绿色边(非匹配边)互换,这样匹配边的数量就加 \(1\)。
结论
一个最大匹配 ⟺ 不存在增广路径
替无可替,现在最大!
三、题目分析
这题乍一看是状压\(DP\),但是题目数据范围是\(100\)比较大,所以要考虑别的思路,由于卡片只能放到相邻的两个格子当中,我们把每个格子看作一个点,相邻两个格子连出一条边,于是这个题就抽象成了最多选多少条边,所有选出的边之间没有公共点,这就是最大匹配问题。
就比如下面这个图,黑色区域是禁止放置的
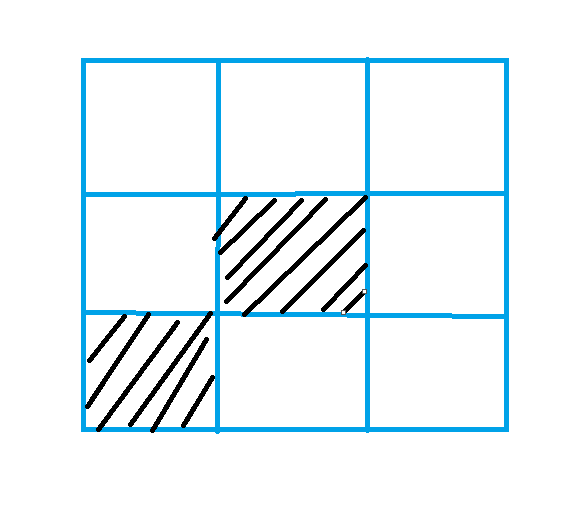
经过匹配之后:

求最大匹配问题可以用匈牙利算法求解,但是用匈牙利算法前提需要图是二分图,所以我们需要判断一下是不是二分图。
一个\(n*n\)的矩阵,我们通过染色把黑色区域看作一个集合,白色区域看作一个集合。
两个集合当中每个点相邻的点的颜色都是不同的,通过染色法判定我们发现这就是一个二分图。而且黑色区域每个点坐标和为偶数,白色区域每个点坐标和为奇数,因此我们就可以用匈牙利算法进行求解最大匹配问题。
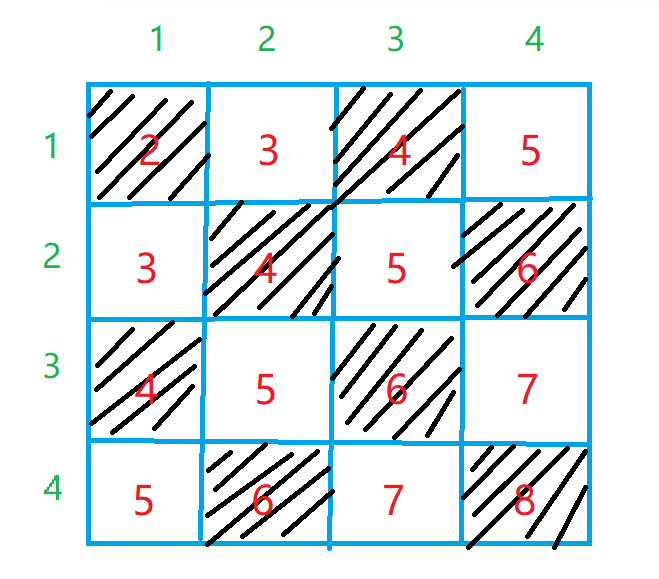
实现步骤:
- 建图(标记禁止放置的点)
- 对二分图中的黑色区域集合进行匹配并且更新答案
- 输出最大匹配数
考虑一个格子\((i,j)\):
- \(i+j\)为偶数:不妨记这样的格子为 白格子
- \(i+j\)为奇数:不妨记这样的格子为 黑格子
如果这个白格子没有被禁止,那么就让它向周围没有被禁止的黑格子连有向边,表示:
如果选择这条边(在这两个格子上放骨牌)会对答案有\(1\)的贡献
显然白格子周围都是黑格子,所以白格子之间不会有边.那么这就是一个 二分图最大匹配的模型 ,跑一下就好了.
时间复杂度
最多\(O(n^2)\)个点,\(O(n^2)\)条边,所以时间复杂度\(O(n^4)\)
三、实现代码
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int n; // n*n的矩阵
int m; // t为禁止放置的格子的数量
int g[N][N]; //某个格子是否是坏点
bool st[N][N]; //在本轮的匹配过程中,是不是已经匹配过了
PII match[N][N]; //和谁匹配
int dx[] = {-1, 0, 1, 0}; //上右下左
int dy[] = {0, 1, 0, -1}; //上右下左
//匈牙利算法求二分图最大匹配 奇数点白,偶数点黑
bool find(int x, int y) {
//这里就看出使用邻接矩阵的优势了,要不怎么上下左右?
for (int i = 0; i < 4; i++) {
int a = x + dx[i], b = y + dy[i];
if (a < 1 || a > n || b < 1 || b > n) continue;
if (st[a][b] || g[a][b]) continue;
st[a][b] = true; //有人相中了
// match[j] == 0:如果j女生以前没有男朋友,那OK,可以
// find(match[j]):如果j的男朋友match[j]可以找其它女生
//白点一伙,黑点一伙,求白向黑的最大匹配边数量
//(a,b)黑点坐标,match[a][b]:此黑点与哪个坐标的白点匹配
// t.x==0 因为N行N列,并且N>=1,所以横纵坐标都是>=1,t.x=0表示说(a,b)这个点还没有被匹配过
//或者,已经被匹配过了白点,但是,可以通过 商量的办法,让其更改男友成功,也是可以牵手的
PII t = match[a][b];
if (t.x == 0 || find(t.x, t.y)) {
//设置女生(a,b)的男朋友是(x,y),逆袭成功!
match[a][b] = {x, y};
return true;
}
}
return false;
}
int main() {
scanf("%d %d", &n, &m);
// m为禁止放置的格子的数量
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
g[a][b] = 1;
}
int res = 0;
// 这里枚举奇数点,枚举偶数点是一样的
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
//如果是奇数点,并且,没有标识为坏点
if ((i + j) % 2 && g[i][j] == 0) {
//利用匈牙利算法,求二分图的最大匹配
memset(st, 0, sizeof st);
if (find(i, j)) res++;
}
//输出最大匹配
printf("%d\n", res);
return 0;
}
四、邻接表解法
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 40010;
int n, m;
int match[N];
bool st[N], g[N];
//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
//匈牙利算法模板
bool find(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (st[j]) continue;
st[j] = true;
if (match[j] == -1 || find(match[j])) {
match[j] = u;
return true;
}
}
return false;
}
int dx[] = {-1, 0, 1, 0}; //上右下左
int dy[] = {0, 1, 0, -1}; //上右下左
int main() {
scanf("%d %d", &n, &m);
memset(h, -1, sizeof h);
memset(match, -1, sizeof match);
while (m--) {
int a, b;
scanf("%d%d", &a, &b);
a--, b--; //因为要做坐标变换,需要下标从0开始,本题下标从1开始,采用减一大法
g[a * n + b] = true;
}
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
if (g[i * n + j]) continue; //出发点有障碍物不可以
if ((i + j) % 2 == 0) continue; //出发点是黑色点不可以
for (int k = 0; k < 4; k++) {
int tx = i + dx[k], ty = j + dy[k];
if (g[tx * n + ty]) continue; //目标点有障碍物
if (tx < 0 || tx == n || ty < 0 || ty == n) continue; //目标点出界
add(i * n + j, tx * n + ty); //加边
}
}
int res = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if ((i + j) % 2 == 1) {
memset(st, 0, sizeof st);
res += find(i * n + j);
}
printf("%d\n", res);
return 0;
}