\(AcWing\) \(396\) 矿场搭建
一、题目描述
煤矿工地可以看成是由 隧道 连接 挖煤点 组成的 无向图。
为安全起见,希望在工地发生事故时 所有挖煤点的工人都能有一条出路逃到 救援出口处
于是矿主决定在 某些挖煤点 设立 救援出口,使得无论哪一个挖煤点坍塌之后,其他挖煤点的工人都有一条道路通向救援出口。
请写一个程序,用来计算 至少 需要设置几个救援出口,以及不同最少救援出口的设置方案总数。
输入格式
输入文件有若干组数据,每组数据的第一行是一个正整数 \(N\),表示工地的隧道数。
接下来的 \(N\) 行每行是用空格隔开的两个整数 \(S\) 和 \(T\),表示挖煤点 \(S\) 与挖煤点 \(T\) 由隧道直接连接。
注意,每组数据的挖煤点的编号为 \(1\)∼\(Max\),其中 \(Max\) 表示由隧道连接的挖煤点中,编号最大的挖煤点的编号,可能存在没有被隧道连接的挖煤点。
输入数据以 \(0\) 结尾。
输出格式
每组数据输出结果占一行。
其中第 \(i\) 行以 \(Case\) \(i\): 开始(注意大小写,\(Case\) 与 \(i\) 之间有空格,\(i\) 与 : 之间无空格,: 之后有空格)。
其后是用空格隔开的两个正整数,第一个正整数表示对于第 \(i\) 组输入数据至少需要设置几个救援出口,第二个正整数表示对于第 \(i\) 组输入数据不同最少救援出口的设置方案总数。
输入数据保证答案小于 \(264\),输出格式参照以下输入输出样例。
二、解题思路
加法原理 与 乘法原理
首先,这个无向图不一定是连通的,所以可以把它分成若干个连通块来讨论,对于每个连通块,标记数最少直接 累加(加法原理),方案数用 乘法原理
缩点
假设我们把所有的 点双 都 缩点, 那么我们一定可以 得到一棵树, 然后我们就会发现:
- 叶子节点( 只含有一个割点的点双 )必须建。因为叶子节点如果不建,一旦割点被爆就死翘翘了
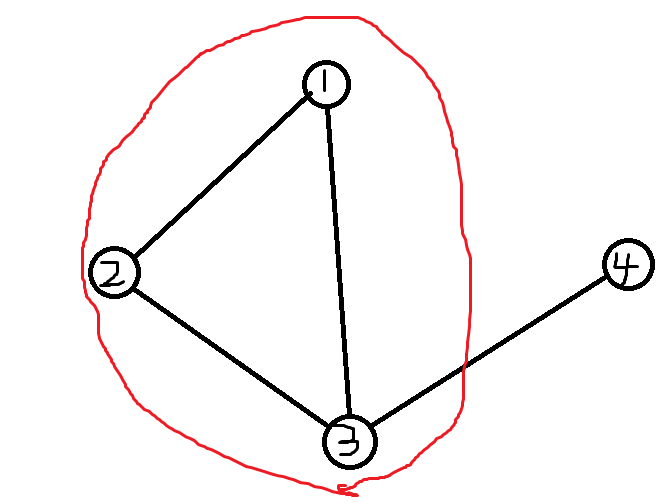
- 非叶节点(含有 两个 或 两个以上的割点 的 点双) 不用建。 因为即使一个 割点 被爆了也可以沿着另一个 割点 走到 另一个叶节点
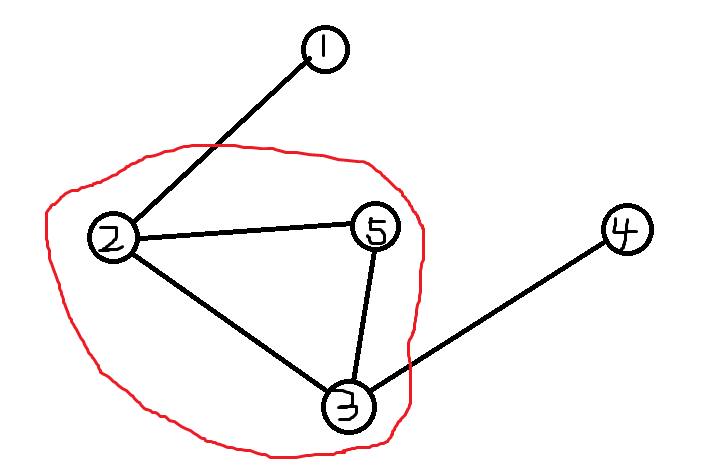
- 还有一种情况就是整个连通块都是点双(即不含割点的点双)
我们讨论点双的大小-
如果只有一个点,那么这个点必须建,数据没有卡这个的点所以我没写(其实是我忘写了 然后还过了)
-
如果有两个或两个以上的点 那么要建两个,一个被爆了还可以走另一个
-
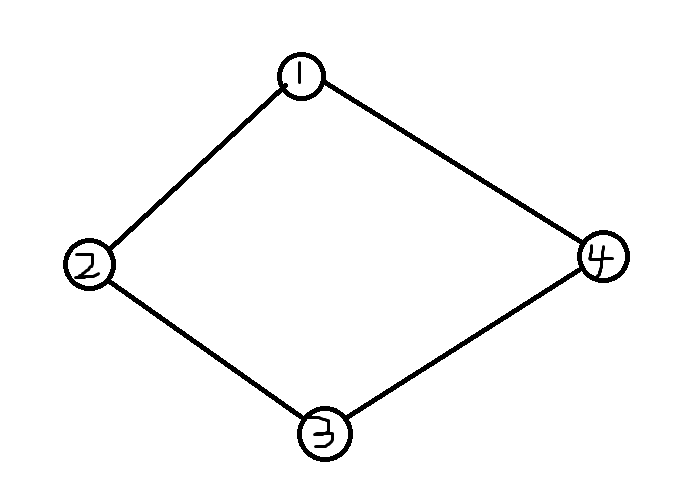
方案数就是乘法原理的问题了 注意叶节点那里出口不能建在割点上
所以先\(Tarjan\)求割点再\(dfs\)一下每个连通块就好了
三、完整代码
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
const int N = 1010, M = 1010;
int n, m;
int dfn[N], low[N], stk[N], timestamp, top, root;
int bcnt;
vector<int> bcc[N]; //双连通分量
bool cut[N]; //哪些节点是割点
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
/*
1. 用tarjan跑出所有的v_bcc和 原图中哪些点是割点
2. 遍历每个v_bcc(边双),考查边双里的割点个数:
(1). 若此边双内包含的割点数>1,则无论哪一个节点被毁,连通性依旧,不用处理。贡献为0
(2). 若此边双内包含的割点数=1,则在分量内任意一点建一个(割点处不用建),一旦分量内建立好的救援出口被毁,
可以通过割点跑到相临的分量中,走别人的救援出口,ans*=bcc.size()-1。贡献为1
(3). 若此边双内包含的割点数=0,则任建两个,ans=bcc.size()(bcc.size()-1)/2。贡献为2
*/
void tarjan(int u, int fa) {
low[u] = dfn[u] = ++timestamp;
stk[++top] = u;
int son = 0;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
if (!dfn[j]) {
son++;
tarjan(j, u);
low[u] = min(low[u], low[j]);
if (low[j] >= dfn[u]) {
int x;
//记录割点的办法
//(1) x不是根节点
//在搜索过程中发现存在x的一个子节点y,满足low[y]≥dfn[x], 那么x是割点
//(2) x是根节点
//在搜索过程中发现 至少存在两个子节点 yi,满足low[yi]≥dfn[x] ,那么x是割点
if (u != root || son > 1) cut[u] = true;
bcnt++;
do {
x = stk[top--];
bcc[bcnt].push_back(x);
} while (x != j); //将子树出栈
bcc[bcnt].push_back(u); //把割点/树根也丢到点双里
}
}
else low[u] = min(low[u], dfn[j]);
}
//特判独立点
if (fa == -1 && son == 0) bcc[++bcnt].push_back(u);
}
int main() {
int T = 1;
while (scanf("%d", &m), m) {
//每次清除上次记录的bcnt连通块中点的向量数组
for (int i = 1; i <= bcnt; i++) bcc[i].clear();
// n:这题太讨厌了,n居然让我们自己取max计算出来,shit~
idx = n = timestamp = top = bcnt = 0;
memset(h, -1, sizeof h); //链表头,全新建图
memset(dfn, 0, sizeof dfn); //每个节点的dfs序时间戳序号
memset(cut, 0, sizeof cut); //清空割点数组
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
n = max(n, a), n = max(n, b); //鄙视一下~
if (a != b) add(a, b), add(b, a);
}
for (root = 1; root <= n; root++)
if (!dfn[root]) tarjan(root, -1); //以root为根开始找出 割点 和 点双
int res = 0; //增加的救援出口个数
ULL num = 1; //增加的救援出口方案数
for (int i = 1; i <= bcnt; i++) { //枚举每个点双
int cnt = 0; //此点双中割点的数量
for (int j = 0; j < bcc[i].size(); j++)
if (cut[bcc[i][j]]) cnt++;
if (cnt == 0) { //如果没有割点
//如果点双中点的数量大于1,救援出口需要在bcc[i].size()中选择两个,一个坏了还可以走另一个
if (bcc[i].size() > 1)
res += 2, num *= bcc[i].size() * (bcc[i].size() - 1) / 2;
else
//如果点双中点的数量等于1,孤立的点,那么必须单独设立一个救援出口
res++;
} else if (cnt == 1) //如果有一个割点
res++, num *= bcc[i].size() - 1; //需要添加一个救援出口
//如果有2个或以上的割点,就不用管了,因为一旦某个割点被毁,可以走另一个
}
printf("Case %d: %d %llu\n", T++, res, num); //救援出口个数,方案数
}
return 0;
}