无向图的双连通分量
一、割点和割边
-
割点:在无向连通图中,删除一个顶点以及和它相邻的所有边,图中的连通分量个数增加,则该顶点称为 割点
-
割边(桥):在无向连通图中,删除一条边,图中的连通分量个数增加,则该条边称为 割边 或者 桥
举个栗子:
割点

割边
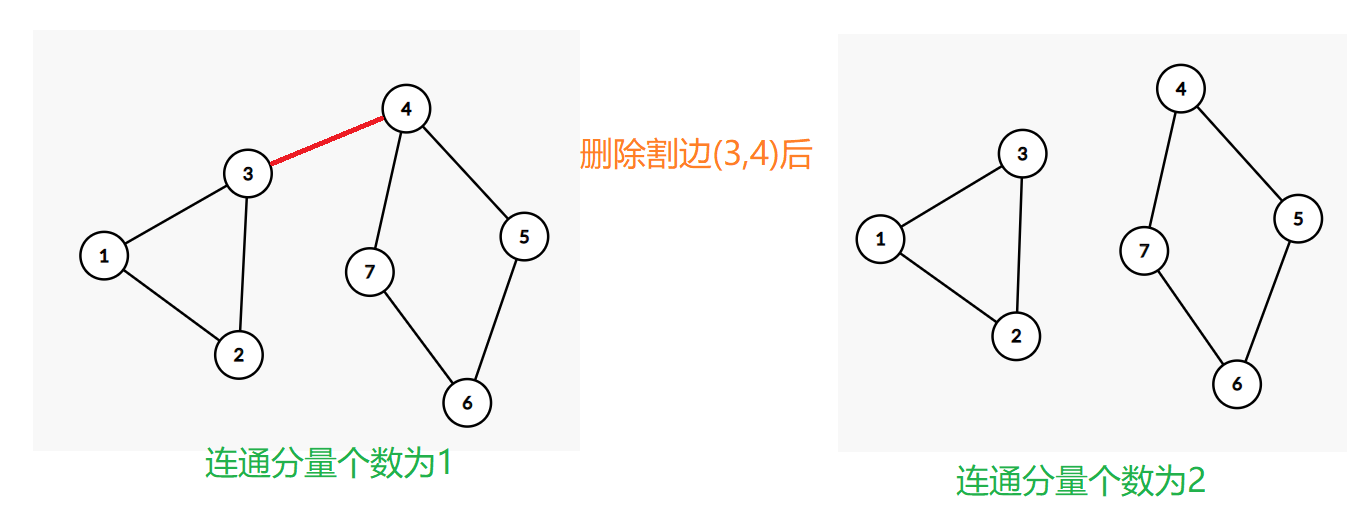
二、边双连通分量 和 点双连通分量
1.边双连通分量
先说不好理解的定义:若一个无向图的点两两间都有两条不重合的路径,那么我们就称这个无向图是 边-双连通 的。
我们看看这个定义又是什么意思,任意两点都有两条不重合的路径,就是说任意点都有两条边可以到达,那么任意去掉一条边,肯定还有另一条边连接,也就是说这个图中不存在割边。所以这个图是边双连通图。
我们画个图来理解:

所谓分支就是一个子图,那么边双连通分支就是说原图中 最大 的一个 双连通分支的子图,一定是最大不然会影响结果。比较好理解,直接上图。

这个图有两个双连通分量, 边双连通分量,就是这么多内容。我们再讲讲边双连通分量缩点。
如果将 边双连通分支 用一个点表示,那么就叫做\(E-DCC\) 缩点 。
经过缩点后建的图必然不存双连通分量,图中存在的边都不在双连通分支中,也就是说缩点后的边都是桥。

黄海感悟:因为桥是一条割边,也就是唯一的一条通路,其它有多条通路的点都缩成了一个点,剩下的这条边,一定是割边,是无向边。
2.点双连通分量
定义:任意两条边都在一个简单环中。
就是说没有割点。还是画图吧!

这两个最大连通子图就是点双联通分支,类比边双连通分支。
也就是说 经过 缩点 后的图中的点除了只有一条边的的点都是割点。
比如\(A,B\)都是缩点后形成的新点,它们俩都是只有一条边连向割点,而割点肯定有最少两条边,\(5\)就是割点。

三、求割点和割边
\(Tarjan\)算法除了栈还引入了\(2\)个数组,分别是:
- \(dfn[N]\) 节点的 时间戳,用来 标记节点访问的先后顺序 以及 是否被访问过, 理解为自己的出生日期。
- \(low[N]\) 当前 环 里最先被访问到的节点,相当于 当前这个连通分量里的根, 理解为你家老祖宗的出生日期。
割点判定
(1) \(x\)不是根节点
在搜索过程中发现存在\(x\)的一个子节点\(y\),满足\(low[y] ≥ dfn[x]\), 那么\(x\)是割点
(2) \(x\)是根节点
在搜索过程中发现 至少存在两个子节点 \(y_i\),满足\(low[y_i] ≥ dfn[x]\) ,那么\(x\)是割点
先来看 第一种,\(x\)不是根节点 ,分为以下三个式子讨论:
① 如果\(low[y] > dfn[x]\),如下图所示:

② 如果\(low[y] = dfn[x]\),如下图所示:

③ 如果\(low[y] < dfn[x]\),如下图所示:

综上可知,当 \(x\)不是根节点,并且 \(low[y] ≥ dfn[x]\)时,说明节点\(x\)是割点。
再来看 第二种: \(x\)是根节点,分两种情况讨论:
① 如果\(x\)是根节点,但是它 只有一个子节点:

② 如果\(x\)是根节点,但是它 至少有两个子节点:

割边判定
在搜索树上存在\(x\)的一个子节点\(y\),满足\(low[y] > dfn[x]\),说明 无向边\((x,y)\)是 桥 (割边)
分为以下三个式子讨论:
当\(low[y]>dfn[x]\)时:

当\(low[y]=dfn[x]\)时:

当\(low[y]<dfn[x]\)时:

综上,当\(low[y]>dfn[x]\)时,才能说明边\((x,y)\)是一条割边
四、成对变换
注意,在无向图中,求割边时,不需要考虑从子节点到父节点之间的边!!
原因如下:

为了解决这此的问题,我们使用了成对变换的办法:
对于非负整数\(n\):
当\(n\)是 偶数,\(n\) ^ \(1=n + 1\)
当\(n\)是 奇数,\(n\) ^ \(1=n − 1\)
这一性质经常用于图论邻接表中 边集 的存储。在具有无向边的图中把一条正反方向的边分别存储在邻接表数组的第\(n\)与\(n + 1\)位置(其中\(n\)是偶数),那么就可以通过 ^ \(1\)运算获得与当前边\((x,y)\)所反向的边\((y,x)\)的存储位置了(存储位置也就是这条边的编号)
如下图:

从中我们发现 成对变换 可以 帮助我们在求割边时避免从子节点走回到父节点 。
\(Q\):如何理解割边的代码模板中的i!=(from^1)呢?
答:就是为了不走回头路!
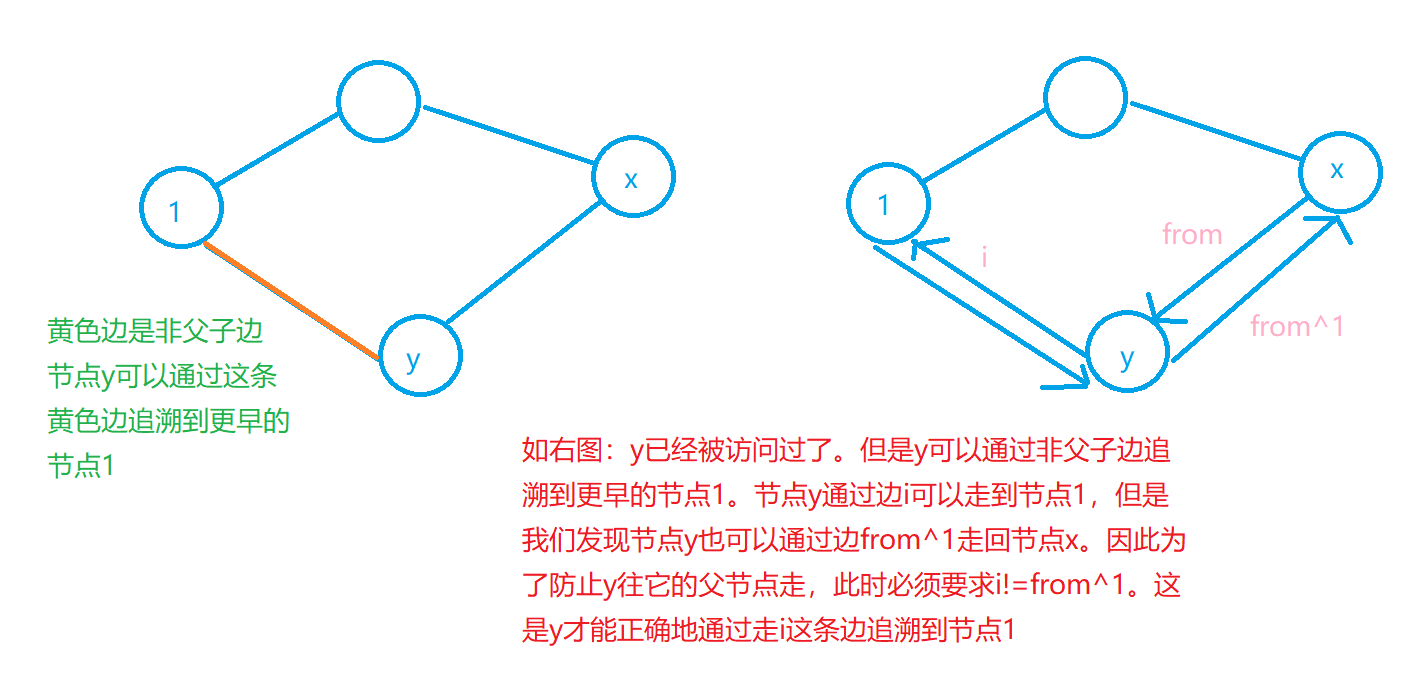
五、【模板】割边
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, M = 4e6 + 10;
//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int dfn[N], low[N], timestamp, root;
set<int> S;
void dfs(int u, int fa) {
low[u] = dfn[u] = ++timestamp;
int son = 0;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
if (!dfn[j]) {
son++;
dfs(j, u);
low[u] = min(low[u], low[j]);
//记录割点
if (u != root && low[j] >= dfn[u]) S.insert(u);
if (u == root && son >= 2) S.insert(u);
}
low[u] = min(low[u], dfn[j]);
}
}
int n, m;
int main(void) {
scanf("%d %d", &n, &m);
memset(h, -1, sizeof(h)); //链表的初始化
for (int i = 1; i <= m; i++) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
for (root = 1; root <= n; root++)
if (!dfn[root])
dfs(root, root);
printf("%d\n", S.size());
for (auto i : S)
printf("%d ", i);
return 0;
}
六、【模板】割点
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, M = 4e6 + 10;
//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int dfn[N], low[N], timestamp, root;
set<int> S;
void dfs(int u, int fa) {
low[u] = dfn[u] = ++timestamp;
int son = 0;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
if (!dfn[j]) {
son++;
dfs(j, u);
low[u] = min(low[u], low[j]);
//记录割点
if (u != root && low[j] >= dfn[u]) S.insert(u);
if (u == root && son >= 2) S.insert(u);
}
low[u] = min(low[u], dfn[j]);
}
}
int n, m;
int main(void) {
scanf("%d %d", &n, &m);
memset(h, -1, sizeof(h)); //链表的初始化
for (int i = 1; i <= m; i++) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
for (root = 1; root <= n; root++)
if (!dfn[root])
dfs(root, root);
printf("%d\n", S.size());
for (auto i : S)
printf("%d ", i);
return 0;
}
七、【模板】边双连通分量
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, M = 4e6 + 10;
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
//边双模板
int dfn[N], low[N], stk[N], is_bridge[N], timestamp, top, root;
int bcnt;
vector<int> bcc[N];
void tarjan(int u, int from) {
dfn[u] = low[u] = ++timestamp;
stk[++top] = u;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!dfn[j]) {
tarjan(j, i); // j:点,i:哪条边
low[u] = min(low[u], low[j]);
} else if (i != (from ^ 1))
low[u] = min(low[u], dfn[j]);
}
if (dfn[u] == low[u]) {
++bcnt; //边双数量+1
int x;
do {
x = stk[top--];
bcc[bcnt].push_back(x); // 记录边双中有哪些点
} while (x != u);
}
}
int n, m;
int main() {
memset(h, -1, sizeof h);
scanf("%d %d", &n, &m);
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
if (a != b) add(a, b), add(b, a);
}
for (root = 1; root <= n; root++)
if (!dfn[root]) tarjan(root, root);
//个数
printf("%d\n", bcnt);
for (int i = 1; i <= bcnt; i++) {
printf("%d ", bcc[i].size());
for (int j : bcc[i]) printf("%d ", j);
printf("\n");
}
return 0;
}
八、【模板】点双连通分量
点双连通分量的求法与边双连通分量的求法不一样。
割点可以包含在点双里。
点双连通分量的求法
1)若某个点为 孤立点,这个点肯定是点双。
2)其他的点双连通分量大小至少为\(2\)个点。
与强联通分量类似,用一个栈来维护:
1、如果这个点第一次被访问时,把该节点进栈;
2、当割点判定法则中的条件 dfn[u]<=low[j]时,无论x是否为根,都要:
- 从栈顶不断弹出节点,直至节点
j被弹出 - 刚才弹出的所有节点与节点
u一起构成一个v-DCC。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, M = 4e6 + 10;
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
//点双模板
int dfn[N], low[N], stk[N], timestamp, top, root;
vector<int> bcc[N];
int bcnt;
void tarjan(int u, int fa) {
low[u] = dfn[u] = ++timestamp;
stk[++top] = u;
int son = 0;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
if (!dfn[j]) {
son++;
tarjan(j, u);
low[u] = min(low[u], low[j]);
if (low[j] >= dfn[u]) {
int x;
bcnt++;
do {
x = stk[top--];
bcc[bcnt].push_back(x);
} while (x != j); //将子树出栈
bcc[bcnt].push_back(u); //把割点/树根也丢到点双里
}
}
low[u] = min(low[u], dfn[j]);
}
//特判独立点
if (fa == -1 && son == 0) bcc[++bcnt].push_back(u);
}
int n, m;
int main() {
memset(h, -1, sizeof h);
scanf("%d %d", &n, &m);
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
if (a != b) add(a, b), add(b, a);
}
for (root = 1; root <= n; root++)
if (!dfn[root]) tarjan(root, -1);
//个数
printf("%d\n", bcnt);
for (int i = 1; i <= bcnt; i++) {
printf("%d ", bcc[i].size());
for (int j = 0; j < bcc[i].size(); j++)
printf("%d ", bcc[i][j]);
printf("\n");
}
return 0;
}
九、常见问题
① 割点和桥之间没有任何关系
- 两个割点之间的边一定是桥吗?不一定是,如下图:
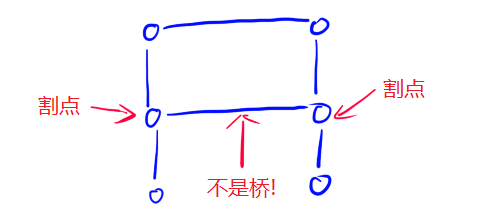
- 一个桥的两个端点一定是割点吗?不一定是,如下图:

② 边连通分量 和 点连通分量 之间也没有任何关系
- 一个图是边连通分量,则它一定是点连通分量吗?不一定是,如下图:
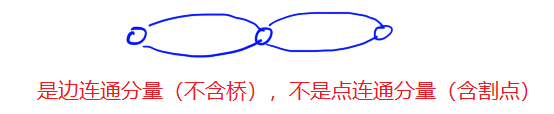
(2)一个图是点连通分量,则它一定是边连通分量吗?不一定是,如下图:

③ 对于一棵树来说,所有的边都是桥,因此树中的每个点都是一个边连通分量;
除叶节点外的所有节点都是割点,因此每条边以及边的两个端点构成的图都是点连通分量。
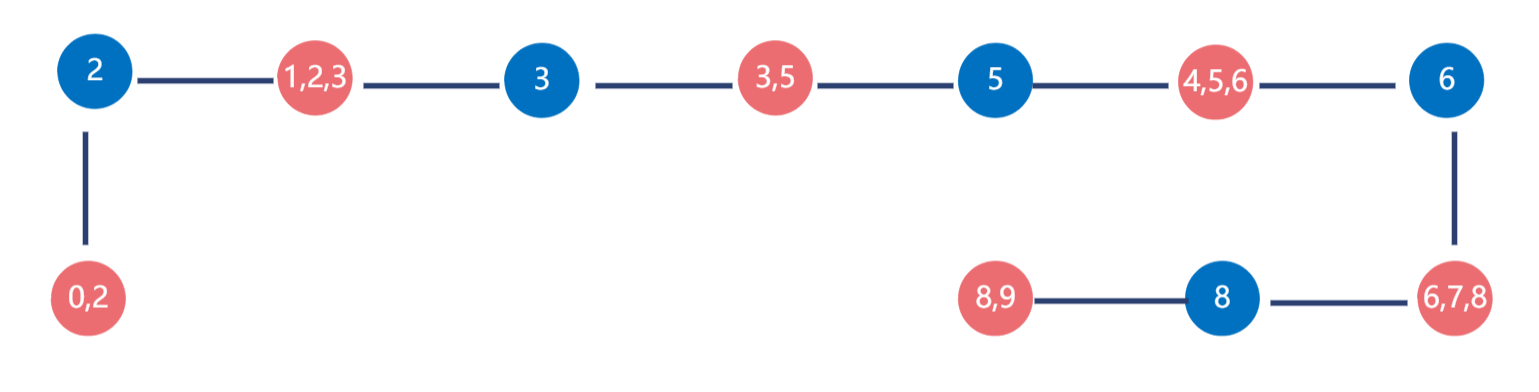
④ 点双连通分量的缩点

再来一个

将(\(1,2,3,4,5\))命名为\(1\)号连通块
将(\(1,6\))命名为\(2\)号连通块
将(\(6,7\))命名为\(3\)号连通块
将(\(6,8,9\))命名为\(4\)号连通块
将割点\(1\)命名为\(5\)号
将割点\(6\)命名为\(6\)号
将每个割点与它从前所属于的连通块进行联边,形如下:

此图也可以参考 这里
一个更复杂的样例

缩点后成为:
十、关于点双和边双的思考
点双 的判定要求比 边双 严格。
点双和边双都是一系列点构成的环, 在不考虑两点一边是点双的特殊情况下,
- ① 点双一定是边双
- ② 边双不一定是点双
- ③ 边双是由一些点双组成的
- ④ 点双内的任意两条边都在同一个简单环中
举个 栗子 方便理解:
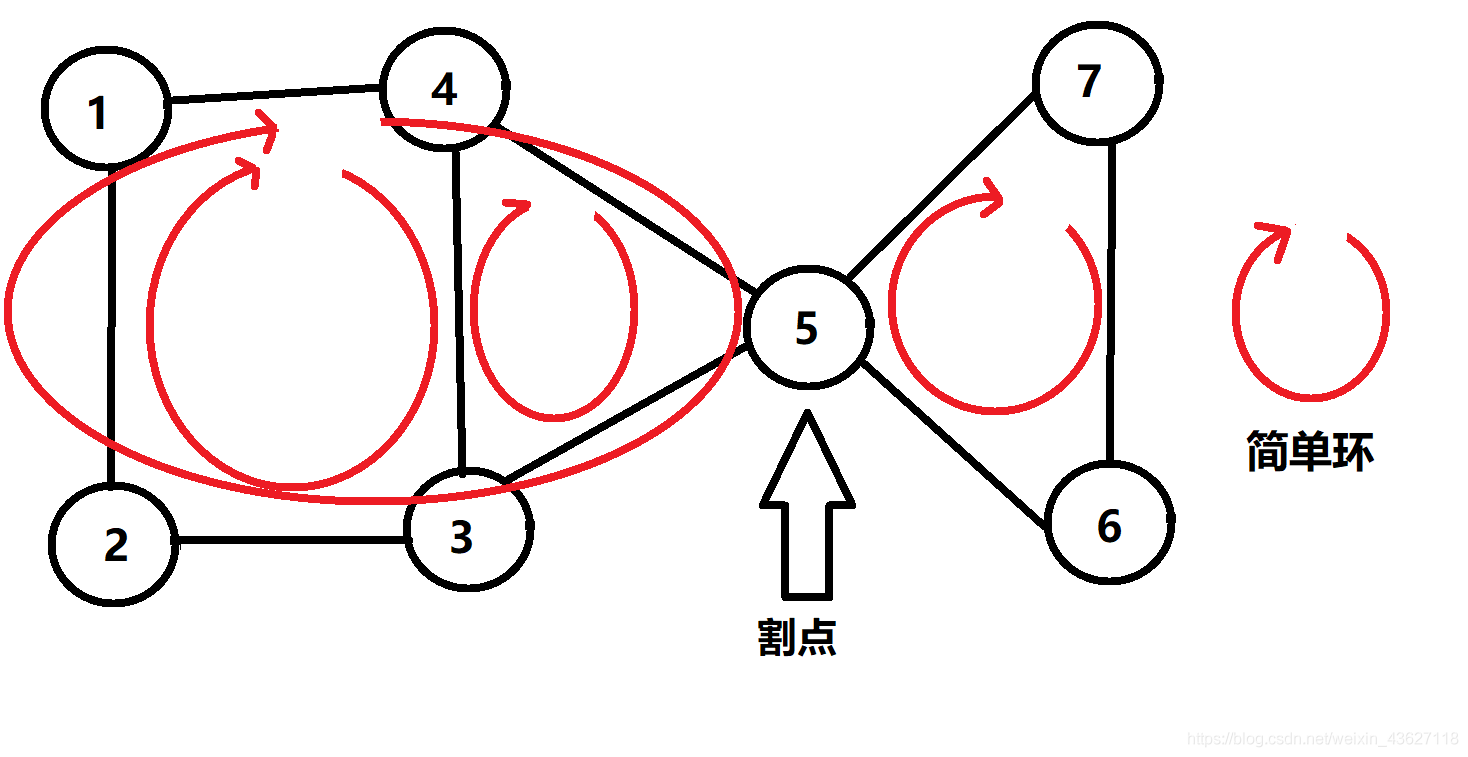
由两个点双组成的边双
十一、练习题 【感觉没有学透,除了胜利我无处可走,干就完了】
\(POJ\) \(2942\) \(Knights\) \(of\) \(the\) \(Round\) \(Table\)
https://blog.csdn.net/weixin_45697774/article/details/109280316
https://blog.csdn.net/bansi8227/article/details/101389413
[USACO06JAN]冗余路径Redundant Paths
题解
https://www.cnblogs.com/PinkRabbit/p/Introduction-to-Block-Forest.html
https://blog.csdn.net/weixin_51216553/article/details/123163433
再整理一遍模板
https://blog.csdn.net/qq_51605889/article/details/124608738