一、题目分析
首先梳理下题意,一个无向图中,有\(N - 1\)条主要边,这么多主要边构成了原图的一棵支撑树。同时还有\(M\)条附加边,每条附加边都会增加一个回路。我们需要做的就是将原图斩为两个不连通的部分,并且需要切断两条边,第一条边必须是主要边,第二条边必须是附加边。
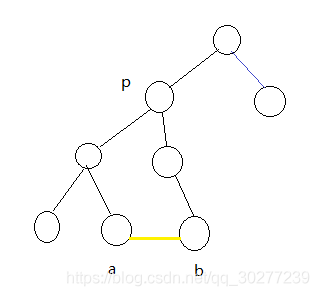
如上图所示,黑色线条连接的边就是主要边,黄色线条连接的边就是附加边。
易知主要边构成了树结构,我们可以依次考虑每个附加边(每次只考虑一条附加边,当其它附加边不存在),然后考虑附加边和树边构成的环。对于这个环上的树边而言,删掉它们之中的任一条后,只能再将那条附加边删掉才能击败\(Dark\)。
可以这样考虑,我们规定树边有一个权值,该权值初始为\(0\),每次枚举一个附加边的时候,都将其所在环的树边的权值加\(1\)。那么在枚举完毕所有附加边之后,权值为\(0\)的边是那种只要将其删去,就直接能击败\(Dark\)(因为它不在任何一个含附加边的环里),所以第一步删去它的方案数有\(M\)个;权值为\(1\)的边是那种将其删去后,还需要删掉\(1\)条附加边才能击败\(Dark\),所以第一步删去它的方案数有\(1\)个;而权值大于\(1\)的边是删去之后无法击败\(Dark\)。
所以问题转化为如何快速实现将树上的某条路径权值都加上某个数\(c\),和如何求出每条边最后的权值。这可以用树上差分(边权)来做:
构造一个差分树,该树和原树的点集和边集一模一样。先对每个点\(v\)开一个点权\(d[v]\),初始为\(0\),如果要将路径\(a\sim b\)这条树上路径的所有边权重都加上\(c\),那么我们可以将\(d[a]\)和\(d[b]\)都加上\(c\),并且\(a\)和\(b\)的最近公共祖先\(p\)的点权\(d[p]\)减去\(2c\)。那么原树某条边的边权就等于差分树中该边指向的深度更深的节点的子树点权之和。
二、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 200010;
int depth[N], f[N][22];
int n, m, d[N];
int ans;
//邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
//树上倍增
void bfs(int t) {
queue<int> q;
q.push(t);
depth[t] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!depth[j]) {
depth[j] = depth[u] + 1;
q.push(j);
f[j][0] = u;
for (int k = 1; k <= 20; k++)
f[j][k] = f[f[j][k - 1]][k - 1];
}
}
}
}
//标准lca
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
for (int i = 20; i >= 0; i--)
if (depth[f[a][i]] >= depth[b]) a = f[a][i];
if (a == b) return a;
for (int i = 20; i >= 0; i--)
if (f[a][i] != f[b][i])
a = f[a][i], b = f[b][i];
return f[a][0];
}
int dfs(int u) {
int res = d[u]; //自己的点权
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (depth[j] > depth[u]) {
int s = dfs(j);
if (s == 0)
ans += m; //删除任意一条附加条均可
else if (s == 1)
ans += 1; //删除组成环的那条附加边
res += s; //加上自己孩子的点权
}
}
return res; //以u为根的所有点的点权
}
int main() {
int a, b;
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 1; i < n; i++) {
cin >> a >> b;
add(a, b), add(b, a);
}
// lca的准备动作
bfs(1);
//读入附加边
for (int i = 0; i < m; i++) {
cin >> a >> b;
//两个端点的点权+1
d[a]++, d[b]++;
//求两个端点a,b的lca
int p = lca(a, b);
// lca的点权-2
d[p] -= 2;
}
//深度遍历一次,在树上找出所有点权为0或为1的点的个数,就是答案
dfs(1);
printf("%d\n", ans);
return 0;
}