\(AcWing\) \(1090\). 绿色通道
一、题目大意
高二数学《绿色通道》总共有 \(n\) 道题目要抄,编号 \(1,2,…,n\),抄第 \(i\) 题要花 \(a_i\) 分钟。
小 \(Y\) 决定只用不超过 \(t\) 分钟抄这个,因此必然有空着的题。
每道题要么不写,要么抄完,不能写一半。
下标连续的一些空题称为一个空题段,它的长度就是所包含的题目数。
这样应付自然会引起马老师的愤怒,最长的空题段越长,马老师越生气。
现在,小 \(Y\) 想知道他在这 \(t\) 分钟内写哪些题,才能够尽量减轻马老师的怒火。
由于小 \(Y\) 很聪明,你只要告诉他最长的空题段至少有多长就可以了,不需输出方案。
输入格式
第一行为两个整数 \(n,t\)。
第二行为 \(n\) 个整数,依次为 \(a_1,a_2,…,a_n\)。
输出格式
输出一个整数,表示最长的空题段至少有多长。
二、二分
1、给定某个长度,若该长度满足条件,就变长继续观察,不满足则变短继续观察,直到找到最小符合的长度值,因此使用二分
2、\(check\)函数中,给定最长的空题段的长度是\(mid\),求出满足题意的花费时间最小值\(res\),判断\(res <= t\)是否成立
按二分的思路,我们在\(0\sim n\)之间去尝试寻找,每次折半,努力找出一个最长的空题段长度,此时总的花费时间不超过小\(Y\)的时间限制\(t\)。
换句话说,就是这个长度假设为\(limit\),那么大于这个长度,肯定不会超过\(t\),否则一定超过\(t\)! 先来一个二分+\(DP\)的原始版本,以后思考问题,先不要想什么优化不优化的,先来简单的,理顺了之后再用常见的招式进行优化一下:
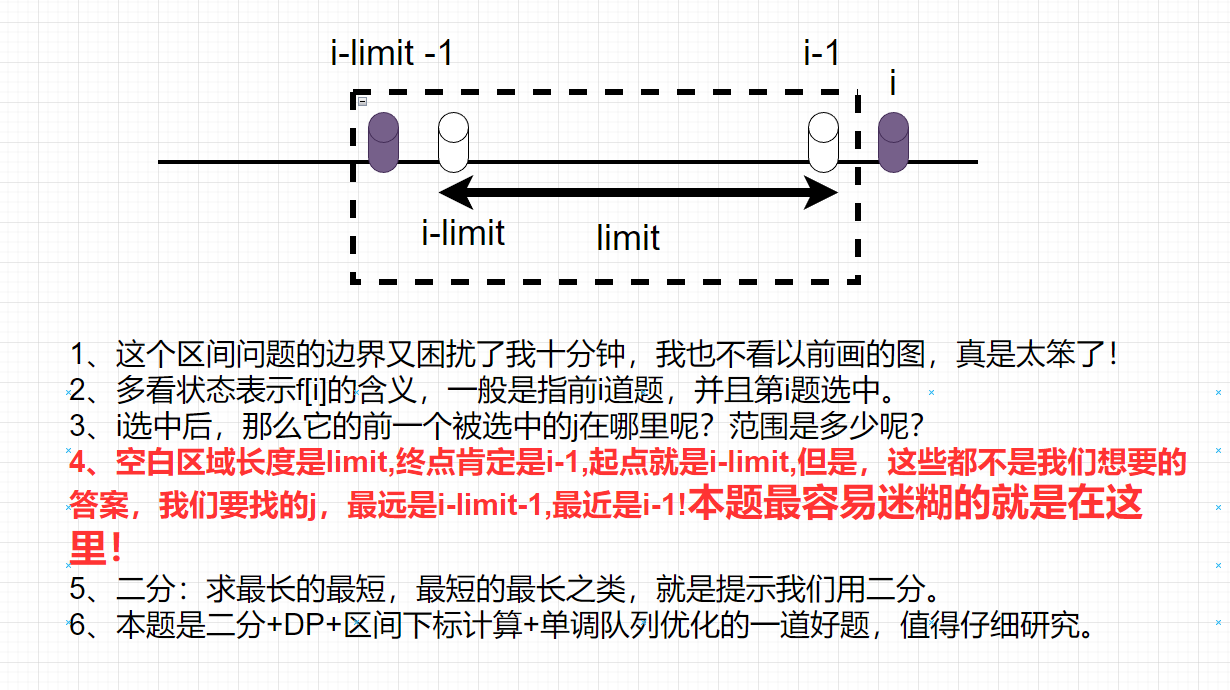
这里有一个小细节问题,就是如果\(i\)选中了,那么它前面最远的可以是哪个?此处与烽火传递不太一样,那么是 在连续 \(m\) 个烽火台中至少要有一个发出信号,翻译一下就是连续\(m\)个中必须有一个,也就是空白区最多是\(m-1\)个!此处是空白区是\(limit\)个,比那个大\(1\)。
二、二分+普通\(DP\)版本
#include <bits/stdc++.h>
using namespace std;
const int N = 50010;
const int INF = 0x3f3f3f3f;
int n, m;
int w[N];
int f[N]; //已经完成前i个,并且第i个被选中 情况下抄袭时间最小值
//暴力+DP 通过了 8/12个数据
bool check(int limit) {
//注意这个初始化,我吃了这个亏~
memset(f, 0x3f, sizeof f);
f[0] = 0;
for (int i = 1; i <= n; i++) //计算前i道题,填表填数据
//注意这个max(0,i-limit-1)
// 此处有两种写法,两种写法的效果是一样的
// 倒序枚举
// for (int j = i - 1; j >= max(0, i - limit - 1); j--)
// 正序枚举
for (int j = max(0, i - limit - 1); j <= i - 1; j++)//第i题肯定是选中的,那么它前面的是哪个位置选中呢?
//这里有区间需要思考一下,limit的含义:是空白,注意是空白,空白,空白
//现在i是选中的,举栗子理解:limit=2 i=10
//则10是选中的,应该9,8可以为空白,因为limit=2嘛
//那么要想求f[10],有这样几种情况讨论一下:
/*
A、0空白,即9被选中
B、1空白,即9不要,8选中
C、2空白,即9,8不要,7选中
共三种情况,最长空白是2,不能再长了,也就是上一个选中的位置范围为10-1=9,10-1-2=7
通用一下就是:i-1,i-1-limit
这个式子的推导练习是关键,一定要特别注意,小心避坑!
*/
f[i] = min(f[i], f[j] + w[i]);
//因为最终的时候,我们可以最后一题不答,可以最后两题不答,也可以最后三题不答,但最多是limit道题不答
//最后[n-limit,n]之间必然得有一题答了吧,这些都是合法解(因为这时可以理解为全部讨论完毕了),我们只要找出最小的就是答案
int res = INF;
for (int i = n - limit; i <= n; i++) res = min(res, f[i]);
//最小值比m小的话,那么就是有可行解,我才不管是不是有其它的值也比m小不小!
return res <= m;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i];
//最长的空题段∈[1,n]
//二分(求最长的最小)
int l = 0, r = n; //空段区间长度0~n都有可能,注意此处是带0的,因为可能老师要求每题必答,对吧,你以为隔一题空一题老师能忍,其实人家忍不了!
//事实也证明了这一点,我尝试修改为 int l=1,r=n;会挂掉一个测试点!
/*
空白时段的长度越长,花费的时间越少
空白时段的长度越短,花费的时间越长
*/
while (l < r) {
int mid = (l + r) >> 1; //一定要搞清楚mid的含义:模拟的最长空题段长度
if (check(mid)) //如果这个空白长度可以使得整体时间<=m,那么空白长度可以再小一点,这是个弯,好好想想
r = mid;
else
l = mid + 1; //如果现在的长度不能使得时间够用,只能是长度再长一点
}
printf("%d\n", l);
return 0;
}
三、DP优化
很明显。上面的思路是对的,因为可以正常通过\(12\)中的\(7\)个测试点。但其它的\(TLE\)了,我们需要优化一下时间。
因为状态转移方程定义的方式,决定了\(i\)是必选的,那么\(w[i]\)是确定要忍受的代价,整体代价要想最小,只能是前面的代价最小!而\(f[i]\)的所有可用前序状态是:\(i\)左侧\(limit+1\)个范围,也就是要找出这个范围内的\(min(f[j])\) 其中\(i-limit-1<=j<=i-1\)。
单调队列维护的是该区间的最小值,由于滑动窗口不包含\(i\),因此\(f[i]\)需要在\(while\)上方进行更新。

最后别忘了需要在\(n ~ n-limit\)之间去枚举找出最小值做为答案,因为最合理的方案,从后往前看,最后一个位置被选中的可能在上面的每个位置,共\(limit+1\)种可能。
#include <bits/stdc++.h>
using namespace std;
const int N = 50010;
const int INF = 0x3f3f3f3f;
int n, m;
int w[N];
int f[N], q[N];
bool check(int limit) {
int hh = 0, tt = 0;
for (int i = 1; i <= n; i++) {
//画图理解一下这个滑动窗口的大小(x模拟的是最大间隔)
//其实滑动窗口的长度是limit+1
while (hh <= tt && q[hh] < i - limit - 1) hh++;
//直接计算极值
f[i] = f[q[hh]] + w[i];
//i入队列
while (hh <= tt && f[q[tt]] >= f[i]) tt--;//Q:滑动窗口中保存的是什么?A:是保存着i之前limit+1个区间内的f[j]的最小值的单调上升队列!
q[++tt] = i;
}
//答案可能存在于 n,n-2,...n-m中,枚举一下求最少值即可
int res = INF;
for (int i = n - limit; i <= n; i++) res = min(res, f[i]);
//最小值比m小的话,那么就是有可行解,我才不管是不是有其它的值也比m小不小!
return res <= m;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i];
//二分(求最长的最小),就是碰一下区间的长度,大了就变小,小了就变大
int l = 0, r = n; //空段区间长度0~n都有可能
//当我们允许的空白时段的长度越长,那么花费的时间越少
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
printf("%d\n", l);
return 0;
}