AcWing 1075. 数字转换

题目传送门

一、约数和

本题要求求\(1 \sim n\)之间每个数的约数和，那么最暴力的办法：

for(int i=2;i<=n;i++){
  for(int j=1;j<=sqrt(i);j++)
       if(i%j==0) sum[i]+=j;
}

这样的办法，时间复杂度\(n*\sqrt[]{n}\),\(n<=10^5\),也是勉强可以过的。

还有更好的方法：

#include <bits/stdc++.h>

using namespace std;
//利用筛法求约数和
const int N = 1e5 + 10;
int sum[N];

int main() {
    //求约数和的经典办法[模板]
    //求2到n中每一个数的因数和，1不算是因为题意
    int n = 50;
    for (int i = 1; i <= n; i++)        //i是因数
        for (int j = 2; j <= n / i; j++)//j代表i的放大倍数
            sum[i * j] += i;            //i*j的约数和+i

    for (int i = 1; i <= n; i++) cout << sum[i] << " ";
    return 0;
}

这么写的时间复杂度是多少呢？
\(i=1-->n\)次
\(i=2-->n/2\)次
\(i=3-->n/3\)次
.... 这就是调和积数
这就是调和积数，\(n*log(n)\) 比原来的 \(n*\sqrt[]{n}\)要优化好多

二、建图

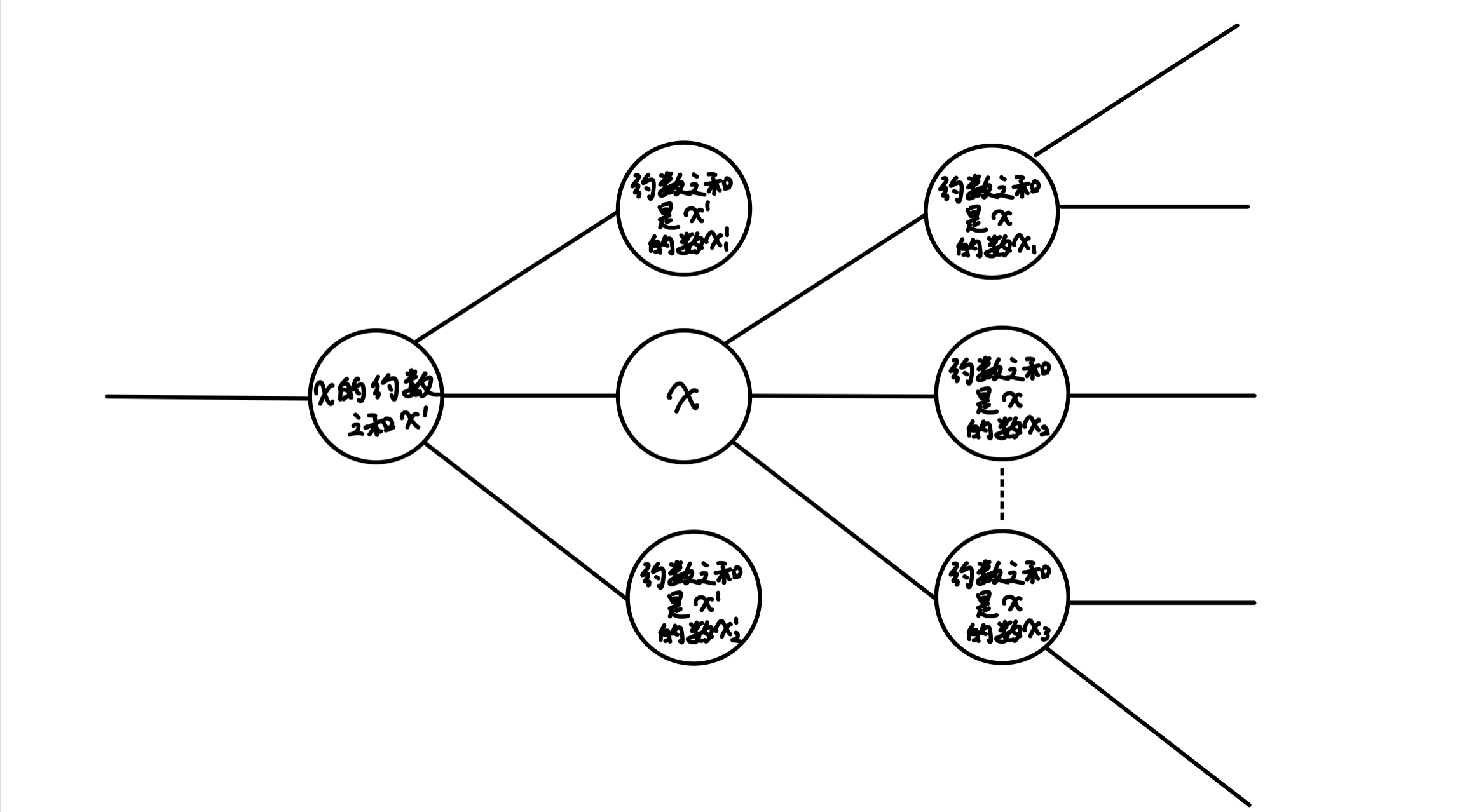每个数$x$，它的约数和$y$,在满足 $y< x$的情况下，才能实现$x->y$的转移。一旦$x$确定了，那么约数和$y$其实也是确定了，而且肯定是唯一的。 反过来，如果给了一个约数和$y$,问它是哪个数的约数和，就不一定了，因为可能有好多数的约数和都是$y$。

建好图后，本题就 等价于 找出一个森林中，直径最长 的树，并求出该树的 直径

那就要用到我们的 树形DP 了，指路 AcWing 1072. 树的最长路径【树形DP】

三、构建有向图求直径

#include <bits/stdc++.h>
//有向图解法
using namespace std;
const int N = 50010;

int n;
int sum[N];
int h[N], e[N], ne[N], idx;
int d1[N], d2[N], res;
int st[N];//标记该点是否被遍历过

//邻接表模板
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

//求树的直径
void dfs(int u) {
    st[u] = true;                       //标识遍历过了
    for (int i = h[u]; ~i; i = ne[i]) { //遍历每条出边
        int j = e[i];
        dfs(j);                       //计算子节点的最大长度
        //如果子节点j的最大长度+1,可以更新u节点的最大长度
        if (d1[j] + 1 >= d1[u]) d2[u] = d1[u], d1[u] = d1[j] + 1;
        else if (d1[j] + 1 > d2[u]) d2[u] = d1[j] + 1;//更新次长节点
    }
    res = max(res, d1[u] + d2[u]);
}

/*
将所有数的约数之和视为这个数的父节点（因为约数和的唯一性）
如果两个数在同一个树上，就代表可以相互转换得到
所以最终是求树上的最长路径
*/
int main() {
    //初始化邻接表
    memset(h, -1, sizeof h);

    cin >> n;
    //求约数和的经典办法[模板] 比试除法的效率要高
    //求2到n中每一个数的因数和，1不算是因为题意
    for (int i = 1; i <= n; i++)//i是因数
        for (int j = 2; j <= n / i; j++)//j代表i的放大倍数 n/i不会溢出
            sum[i * j] += i;    //i*j的约数和+i

    //构建森林
    /**
     每个数的约数之和是唯一的，但同一个数可能是多个数的约数之和。
     因此应该由每个数的约数之和向它本身连边，这样能保证每个点只有一个父节点，
     从而才可以形成一棵树。边反向之后就不一定是树了
     */
    for (int i = 2; i <= n; i++) //数字1没有约数和（本题要求）
        //当约数和小于原数，添加一条由约数和到原数的边，有向边.小数->大数存在边,肯定无环，不用无向图
        if (sum[i] < i) add(sum[i], i);

    //遍历所有未标识为叶子结点的点，即遍历所有根结点
    for (int i = 1; i <= n; i++)
        if (!st[i]) dfs(i);

    //输出
    printf("%d\n", res);
    return 0;
}

四、构建无向图求直径

#include <bits/stdc++.h>

using namespace std;
//无向图解法
const int N = 1e5 + 10;//因为这里是无向图创建图，所以需要记录两倍的边数量，原来的数量假定是N，现在就是2*N
int h[N], e[N], ne[N], idx; //邻接表
int sum[N];                 //约数和数组
int d1[N], d2[N];           //i结点的最长距离与i结点的次长距离
int n;                      //本题给定的数字n
int res;                    //最长转换步骤，也就是树的直径,边权为1,有同条边直径就是几
int st[N];

//邻接表模板
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

//u:从哪个节点出发
//father:上一个节点是谁，防止走加头路
/*
dp算法: 以任何一个点出发, 找到距离该点最远的2条路径, 加起来就是结果. 由于用的是无向边,
所以dfs能够遍历到所有点所有边, 只需要把结果用全局变量更新即可.
*/
void dfs(int u, int father) {
    /*因为本题要从森林中找出所有的树，但因为上面的算法描述说明：如果一个顶点在一个无向树中，则可以求出
     (1)距离该点的最长路径
     (2)距离该点的次长路径
     (3)树的直径=最长路径+次长路径
     如果在计算过程中某些点使用过了，那么就没有再次计算的必要(因为再算也是这个直径，无意义)，可以通过d1[u]是否有值来获取是否使用过。
     */
    st[u] = true;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father)continue;//不走回头路
        //走一下j这条路径
        dfs(j, u);
        //最长路转移
        //d1[u]:u结点的最长路径
        //d2[u]:u结点的次长路径
        if (d1[j] + 1 >= d1[u]) d2[u] = d1[u], d1[u] = d1[j] + 1;
        else if (d1[j] + 1 > d2[u]) d2[u] = d1[j] + 1;//次长路转移
    }
    //更新结果
    res = max(res, d1[u] + d2[u]);
}


int main() {
    //初始化邻接表
    memset(h, -1, sizeof h);
    cin >> n;
    //筛法求出不包含i本身的所有约数和
    for (int i = 1; i <= n; i++)//i是因数
        for (int j = 2; j <= n / i; j++)//j代表i的放大倍数 n/i不会溢出
            sum[i * j] += i;    //i*j的约数和+i

    //无向图建图
    //题意：如果一个数x的约数之和y（不包括他本身）比他本身小，那么x可以变成y，
    //y也可以变成 x。
    //(1)约数和小于本身，可以互相转化
    //(2)注意边界，数字1不存在不包括它本身的约数，也就是不能从数字1引出边到它的约数和
    for (int i = 2; i <= n; i++)    //本题要求:数字1没有约数和
        if (sum[i] < i) add(sum[i], i), add(i, sum[i]);


    //枚举所有根结点
    for (int i = 1; i <= n; i++)
        if (!st[i])dfs(i, -1);

    cout << res << endl;
    return 0;
}

五、理解与感悟

• \(dfs\)写法最好写成\(void\)返回，不要采用\(int\)方式，这样码风统一。此时，采用类似于记忆化的办法，利用数组\(d1[N],d2[N]\)来记录每个\(u\)结点最长距离和最短距离。采用\(int\)返回值时，还需要返回\(d1\),太麻烦了。

• 还管是有向图还是无向图，在遍历可能出现的森林时，需要用\(st[N]\)对已访问过的结点进行标识，防止重复计算，一来可以提高计算速度，二来也可能使结果出错。