AcWing 479. 加分二叉树

题目传送门

一、前导知识

一次讲清二叉树的前序、中序、后序遍历的所有细节

二、题目描述

给定一个含有 \(n\) 个结点的二叉树的 中序遍历 序列中每个节点的 权值

定义一棵 子树 的 分数 为 左子树的分数\(×\)右子树的分数\(+\)根节点的权值

额外规定 空树 的 分数 为 \(1\)

求一种满足该 中序遍历 的建树方案，使得整棵树的 分数 最大

三、解题思路

了解到了遍历情况后，我们就可以根据这些遍历的特点来分析题面。

因为中序遍历为左根右，所以，我们可以得到y总画的这个图

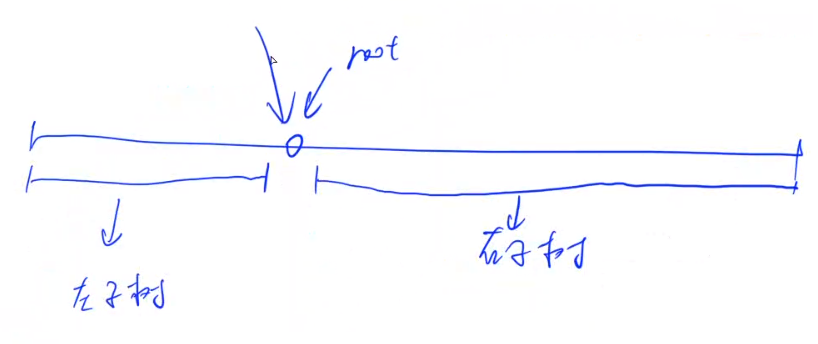
由此图可以发现，我们在找到一个根节点时，此根节点的左子树就是\([1,root-1]\)，右子树就是\([root+1,n]\)。根据这个我们就可以联想到区间\(DP\)。

类比一下最简单的区间\(D\)P试题：合并石子。在一个普遍的时刻，最后一次的中间点选择是不一样的变数，枚举最后一次的中间点选择是关键。

本题中，根的选择是关键，需要枚举根的位置。

再根据闫氏DP分析法来看

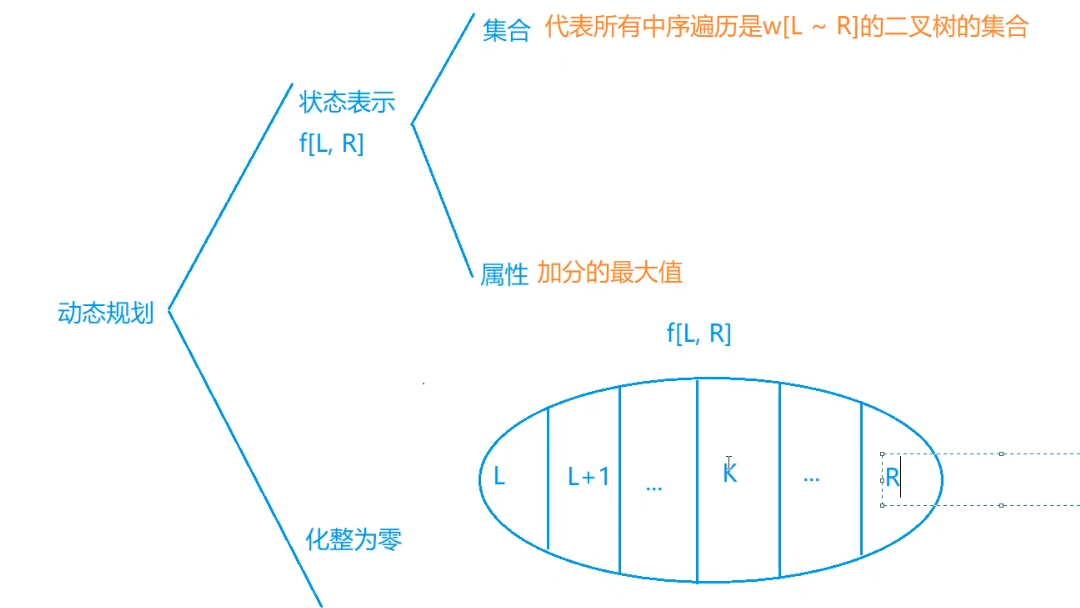
我们根据题目可知我们要求得属性为\(max\)，我们定义一个数组\(f[l][r]\)为在\([l,r]\)之间的最大加分值。
所以，我们也就得到了状态转移方程\(f[i][j]=max(f[i][k - 1]*f[k + 1][j]+a[k])\), \(k\)为根节点。所以就在枚举区间的过程中进行状态转移即可。

此题还有一个难点就是需要记录一下路径，所以我们可以开一个\(g[l][r]\)，记录\([l,r]\)上的根节点。就可以根据我们记录的根节点进行递归求先序遍历，输出即可。

四、实现代码

#include <bits/stdc++.h>

using namespace std;
//区间DP问题怎么记录路径
const int N = 50;

int n;
int w[N];       //权值
int f[N][N];    //区间DP数组
int g[N][N];    //记录i,j区间内的最大得分，是在k这个节点为根的情况下获得的

//前序遍历输出路径
void dfs(int l, int r) {
    if (l > r) return;
    int k = g[l][r];                  //根结点
    printf("%d ", k);          //输出根结点
    dfs(l, k - 1);                  //递归输出左子树
    dfs(k + 1, r);                  //递归输出右子树
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];

    //遍历每一个长度区间
    for (int len = 1; len <= n; len++)
        //遍历左端点位置
        for (int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;            //计算右端点
            for (int k = l; k <= r; k++) {  //枚举每个分界点
                //根据题意特判
                int left = k == l ? 1 : f[l][k - 1]; //左子树为空，返回1
                int right = k == r ? 1 : f[k + 1][r];//右子树为空，返回1
                //计算得分
                int score = left * right + w[k];
                if (l == r) score = w[k];//如果是叶子，叶子的加分就是叶节点本身的分数，不考虑它的空子树。
                //因为需要记录第一个取得最大的值(字典序最小)，不能使用Max
                if (f[l][r] < score) {
                    f[l][r] = score;
                    g[l][r] = k;    //记录l~r区间的最大得分是由哪个根节点k转化而来
                }
            }
        }
    //输出
    printf("%d\n", f[1][n]);
    //利用递归，输出路径
    dfs(1, n);
    return 0;
}