一、前序DP知识复习
二、闫式DP分析法
\(Q\):\(dp\)为什么能优化算法呢?
\(A\):因为它是枚举了所有方案,它枚举的比较聪明。暴搜是枚举每一种方案,它的算法复杂度是指数级别的。\(DP\)之所以能优化,是因为它用了一个数来表示一类东西。就是状态\(f[i][j]\)可以来表示一类东西,每一次都是在集合基础之上做出选择,而不是一事一议。
三、使用闫式DP分析法分析本题
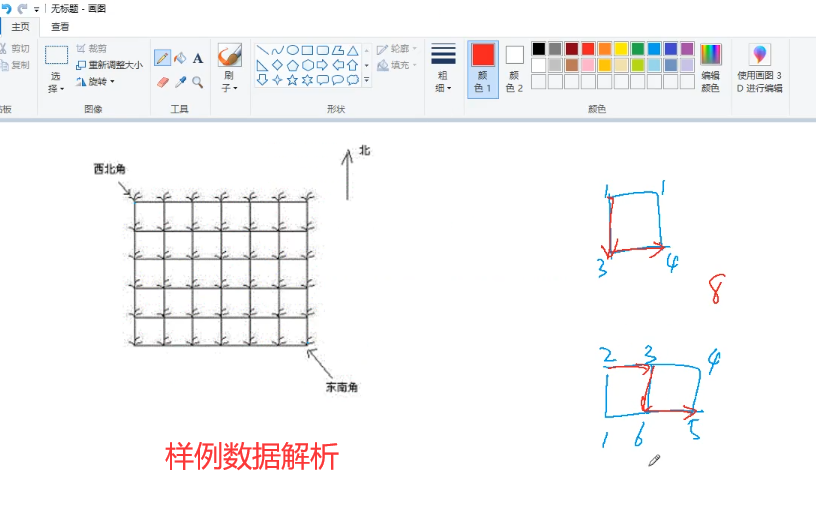
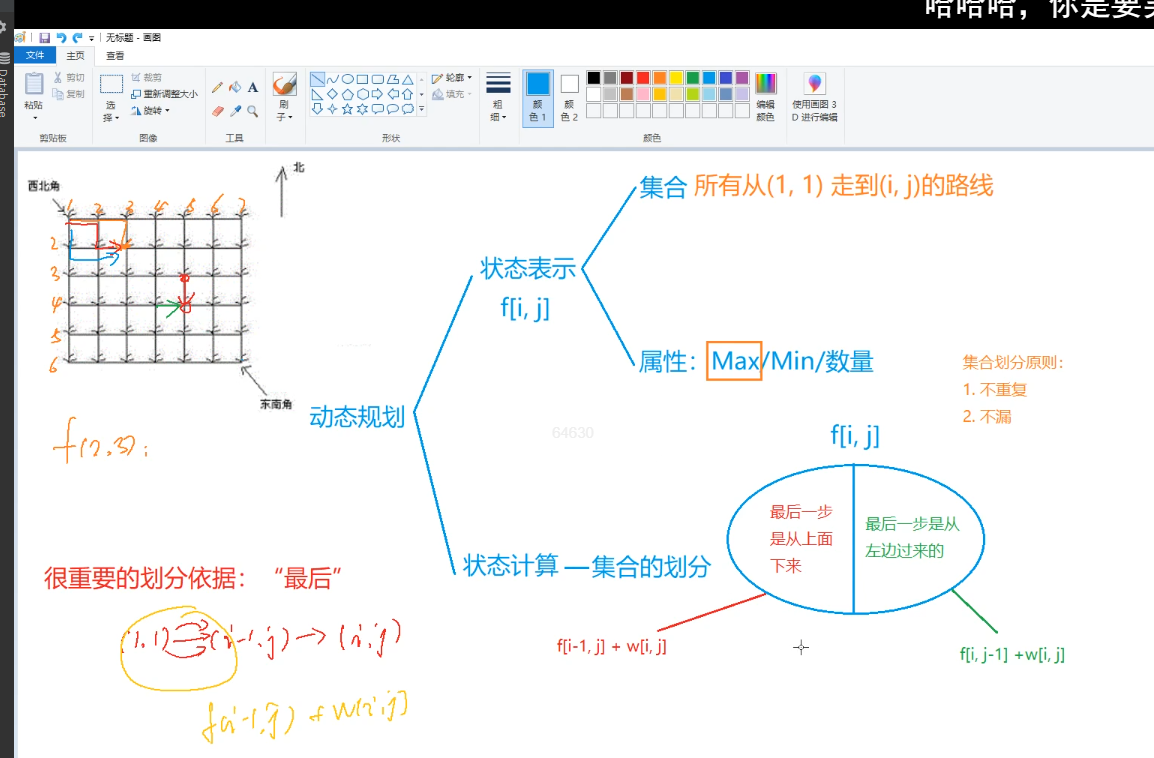
本题的集合含义\(f[i][j]\)来表示所有从\((1,1)\)走到\((i,j)\)的路线,\(f[i][j]\)的值:所有路线中花生数量之和最大值。
对比一下:
传统方式:从\((1,1)\)走到\((i,j)\)的最大值。
闫氏\(DP\)思考法:从\((1,1)\)走\((i,j)\)所有路线的最大值。
总结一下,就是多了一个中间的集合状态,所有路线,但就是因为增加了这个中间的集合,使得下一步的分析工作变得有决策性,而不是一事一议,牛就牛在这里!
结果:就是\(f[n][m]\)就是解
四、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int w[N][N]; //(i,j)位置花生的数量
int f[N][N];
int T;//一共有T组数据
int n, m;
int main() {
cin >> T;
while (T--) {
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> w[i][j];
//base case,思考递推的开始点,它的最优解是什么,一般是自己或者是0
f[1][1] = w[1][1];
//dp 从上到下,从左到右,就是小猫要走的路线, 一路递推下去就是答案
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
//每一个位置 ,都依赖它的上方元素和左侧元素,一路都在取舍
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
//输出结果
printf("%d \n", f[n][m]);
}
return 0;
}