一、算法原理

二、实例模拟
具体的我们以一组无序数列\(\{14,12,15,13,11,16 \}\)为例分解说明,如下图所示:
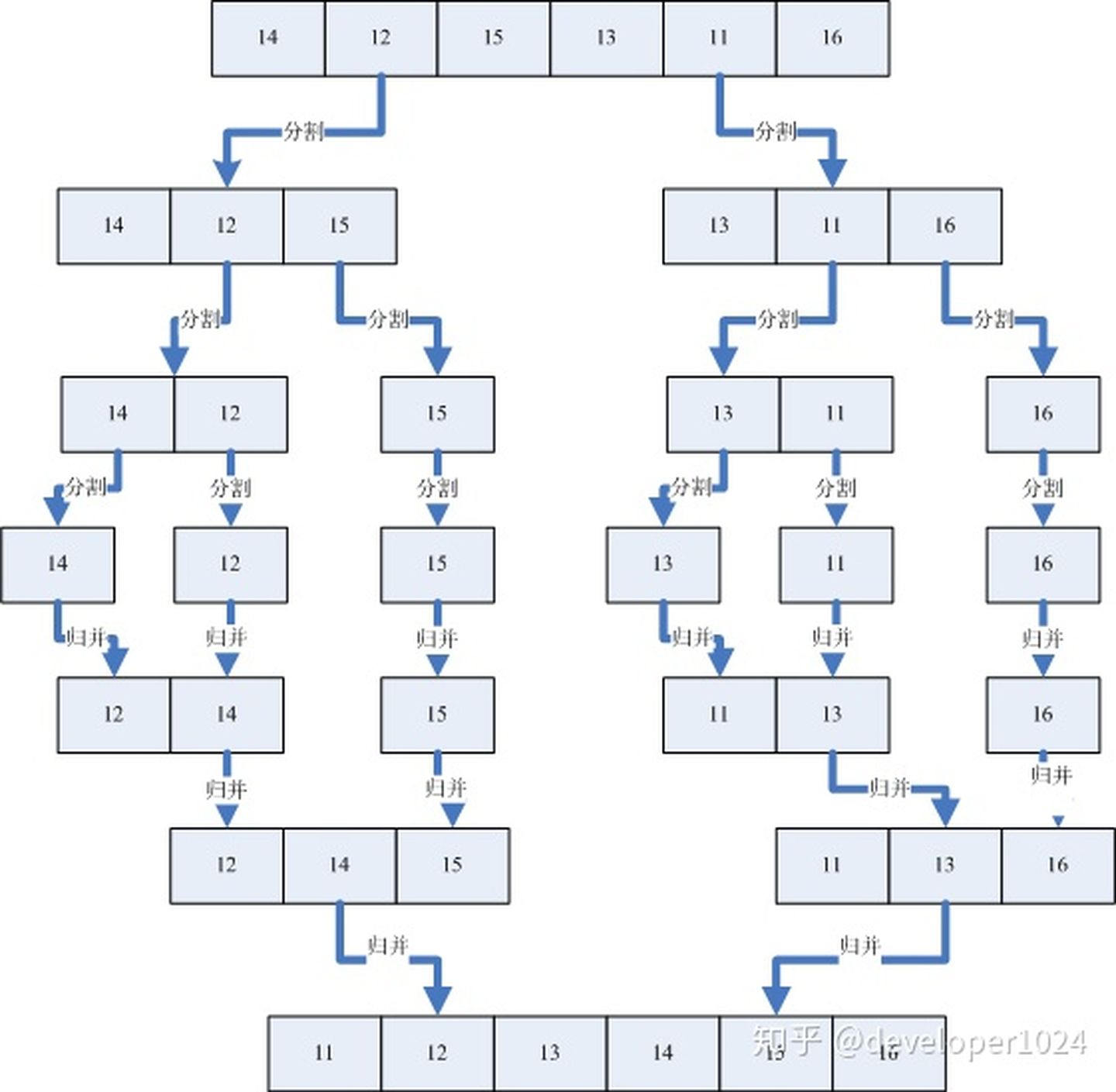
上图中首先把一个未排序的序列从中间分割成\(2\)部分,再把\(2\)部分分成\(4\)部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
三、代码模板
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int q[N]; //原数组
int tmp[N]; //临时数组
/**
* 功能:归并排序
* @param q 要排序的数组,按地址引用
* @param l 左下标
* @param r 右下标
*/
void merge_sort(int q[], int l, int r) {
//数组空,返回
if (l >= r) return;
//中间位置
int mid = (l + r) >> 1;
//递归左侧
merge_sort(q, l, mid); // mid归前不归后
//递归右侧
merge_sort(q, mid + 1, r); //后面是从mid+1开始的
//在完成归后,并的过程,就是本轮需要自己处理的合并事情
int i = l; //左侧出发点
int j = mid + 1; //右侧出发点
int k = 0; //临时数组下标索引
//双指针,遍历两个子数组,谁小谁进入临时数组
while (i <= mid && j <= r)
if (q[i] <= q[j])
tmp[k++] = q[i++];
else
tmp[k++] = q[j++];
//有剩余的就全部扫进临时数组
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
//将tmp数组数据复制回q数组
for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
int main() {
//读入优化
ios::sync_with_stdio(false);
//输入
int n;
cin >> n;
for (int i = 1; i <= n; i++) cin >> q[i];
//归并排序
merge_sort(q, 1, n); //注意参数为1~n
//输出结果
for (int i = 1; i <= n; i++) printf("%d ", q[i]);
return 0;
}