一、已知后序+中序,求前序
求解步骤:
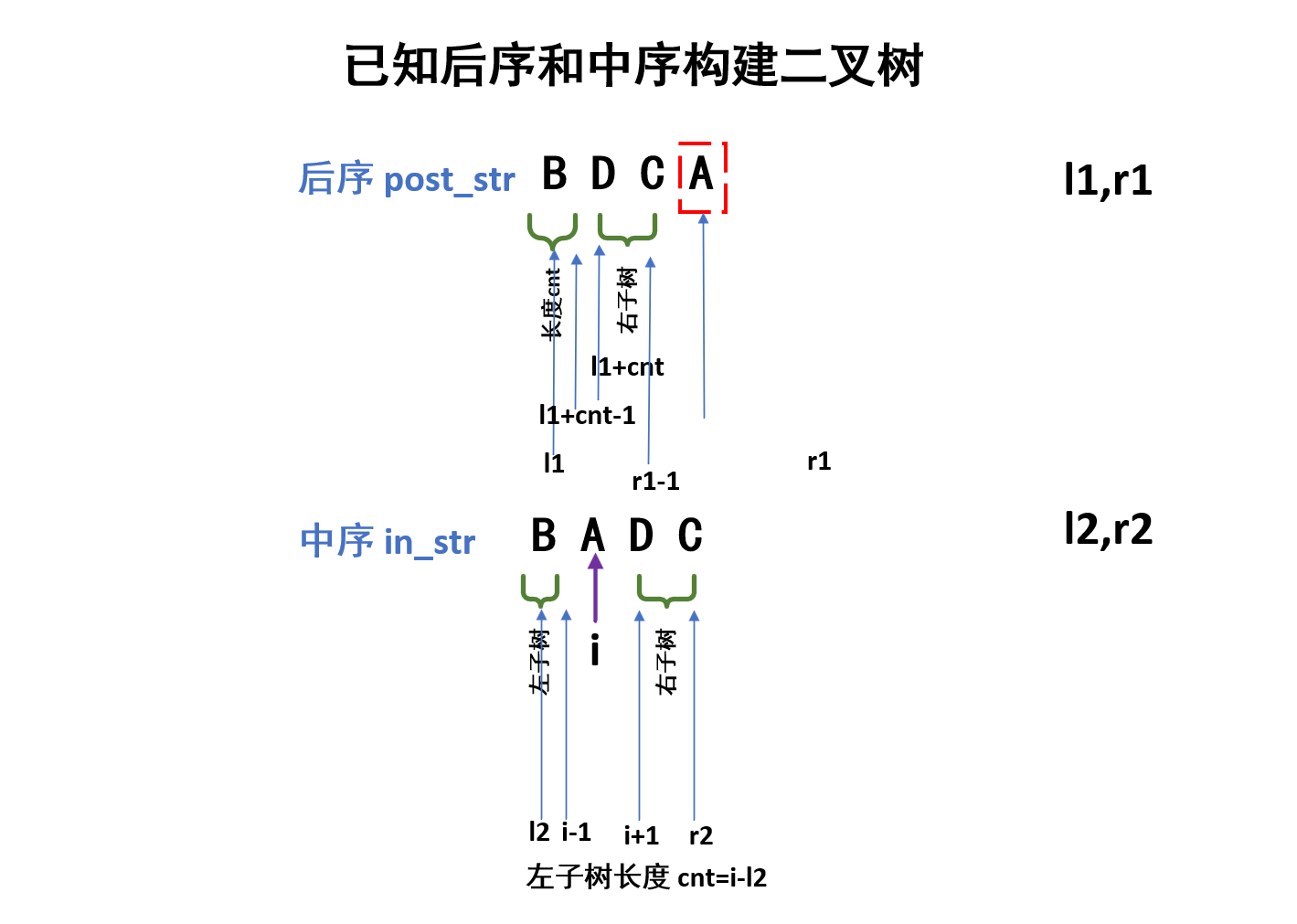
(1)后序遍历的字符串,尾字母是子树的根。
(2)在中序遍历字符串中找到“步骤1查找到的尾字母”,它的左边就是左子树,右边就是右子树,可以计算获得左子树长度(cnt=i-l2)。
(3)在后序遍历字符串中根据左子树长度,获取到左子树子串((l1 -> l1+cnt-1)),右子树((l1+cnt -> r1-1))
(4)递归就可以继续前序输出左右子树。
很多二叉树的题目,不需要真正的还原创建出二叉树,只是根据字符串,不断的递归子串,在递归过程中输出想要的结果,这样更轻量一些,代码更短。
代码原理:
C++代码
#include <bits/stdc++.h>
using namespace std;
string post_str; //后序
string in_str; //中序
//函数定义:输出给定后序遍历、中序遍历字符串的前序遍历字符串
//后序遍历的范围 l1-r1
//中序遍历的范围 l2-r2
//递归只是输出眼前自己力所能及的事情,就是把当前子树的根输出,然后再继续递归调用获取子树的前序遍历字符串
void dfs(int l1, int r1, int l2, int r2) {
//当前为空树 则直接返回,递归终止条件
if (l1 > r1 || l2 > r2) return;
//从中序遍历中找出左树的范围
int i = in_str.find(post_str[r1]);//post_str[r1]是指尾巴是根结点
//左子树节点有多少个
int cnt = i - l2;
//后序遍历的最后一个一定是节点的根,输出根的值
cout << post_str[r1];
// 递归构建左树
// 后序,中序
dfs(l1, l1 + cnt - 1, l2, i - 1);
// 递归构建右树
// 后序,中序
dfs(l1 + cnt, r1 - 1, i + 1, r2);
}
/**
BADC 中序
BDCA 后序
BADC
BDCA
参考答案:ABCD
*/
int main() {
cin >> in_str >> post_str;
int right = in_str.size() - 1; //right索引:因为是0开始,所以要-1
dfs(0, right, 0, right);
return 0;
}
二、已知前序+中序,求后序
P1827 [USACO3.4]美国血统 American Heritage 题解
https://www.cnblogs.com/littlehb/p/15088448.html
三、已知前序+后序,求中序个数
P1229 遍历问题
https://www.luogu.com.cn/problem/P1229
https://www.cnblogs.com/littlehb/p/15099843.html