P3397 地毯题解

题目传送门

一、题意理解

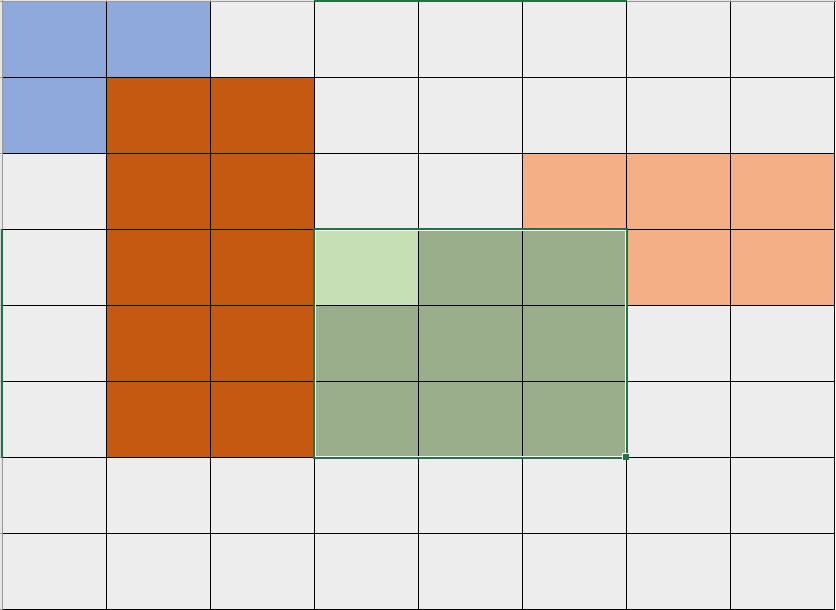
画图理解，就是一个(8 imes 8)的房间，里面有(4)块地毯，覆盖的范围如图所示，但它们之间有交集，问我们每个小块被覆盖了几次。

二、数组模拟

上来一看，无脑二维数组模拟啊，用(a[N][N])来模拟这块地毯，内容值：被盖上的次数。打一遍，提交!

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int a[N][N];
int n, m;

int main() {
    cin >> n >> m;
    while (m--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        for (int i = x1; i <= x2; i++)
            for (int j = y1; j <= y2; ++j)
                a[i][j]++;
    }
    //输出结果
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++)
            printf("%d ", a[i][j]);
        printf("
");
    }
    return 0;
}

直接(AC)!书中说原题的数据范围较大，需要使用二维前缀和的思路，其实这么说是不严谨的，是二维差分。

本题数据范围为(n<=1000,m<=1000)。当(n<=1000,m<=1000000)甚至(m<=10000000)怎么办呢？

我们来观察一下上面的代码存在哪些效率上的问题。因为每一块地毯，都需要进行双重循环，如果每块的长宽较大，就是需要算的数量增大很多，容易(TLE)。

这时，我们看看能不能降一下复杂度解决此问题：

这是一个非常典型的在二维数组中区域加减某个数字的问题，就是二维差分的模板。

一维前缀和与二维前缀和

一维差分与二维差分

三、二维差分

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int a[N][N];
int b[N][N];
int n, m;

/**
 * 功能：二维差分的模板
 * @param x1 开始点横坐标
 * @param y1 开始点纵坐标
 * @param x2 结束点横坐标
 * @param y2 结束点纵坐标
 * @param c  要加的值
 */
void insert(int x1, int y1, int x2, int y2, int c) {
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main() {
    cin>>n>>m;
    while (m--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        //对比二维差分的表示，四个加法运算，优化掉双重循环
        insert(x1, y1, x2, y2, 1);
    }

    //通过二维差分，还原成原始数组
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
            printf("%d ", a[i][j]);
        }
        printf("
");
    }
    return 0;
}