1.选择题
【题目要求】
只允许使用四则运算,求出任意正数 $x$ 的自然对数 $ln (x)$
【输入】
一个数 $x,(0<x<10^9)$
【输出】
一个数 $ln (x),$保留 6 位小数。
【时空限制】
$t leq 1 sec;m leq 128 MiB$
2.填空题
【题目要求】
本题允许使用四则运算和$exp$函数,给出两个数$a,b,(0<a,b<10^9)$,求$f(x)$在区间$[0,+ infty )$的最大值。其中
$f(x)=dfrac{ax^3-bx^2}{e^{x^2- sin (x) -1}}$
由于今天小红比较开心,所以特地帮你们把这个函数的导函数求了出来:
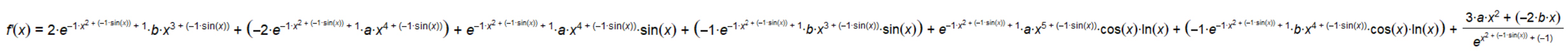
(懒得打$LaTeX$公式了,就这么着看)
【输入】
两个数$a,b$
【输出】
一个数$f(x)_{max}$,保留6位小数。
【时空限制】
$t leq 1 sec;m leq 128 MiB$
3.解答题(物理向)
【题目要求】
平面直角坐标系中有$n$个质点,给出各质点的坐标$(x_i,y_i)$与质量$m_i$,求它们质心的坐标$(x_{sigma},y_{sigma})$。
本题不会编程的可手算,保留一位小数即可。
此题允许使用四则运算和$exp$函数
【输入】
第一行一个数$n,(n leq 10)$,表示$n$个质点。
第$2 ext{~}n+1$行三个数,表示各个质点的坐标$x_i,y_i$和质量$m_i$。
【输出】
两个数$(x_{sigma},y_{sigma})$,保留3位小数。
【时空限制】
$t leq 1 sec;m leq 128 MiB$
【评分细则】
令标准答案为$std$,你的答案为$ans$:
得分 $score=P((std pm ans ext{~} pm infty ), x ext{~} N(std,0.01) $
(对于手算,得分$score=P((std pm ans ext{~} pm infty ) ,x ext{~} N(std,1) $)