以前做比赛的方法有些不对,只顾做比赛,平时也没做题,比赛做过之后就不管了,这样做不到学习的目的,只是练个手熟罢了,因此以后参加的比赛,要认真做好赛后AK的工作。
A. Heroes
题意大致这样,有7个人,要分成3组,去打Boss,对于三组有经验(A, B, C),存在这样的关系,a like b,要分组使得7个人每个人获得的经验差值就小,然后要使得3组中,like关系数最多。
暴力枚举7个人的分组情况,然后统计上述参数就可以了,复杂度O(3^7 * 7 * 7),联想到三进制进行枚举会较好实现,我用DFS去枚举分组情况。
#include <iostream>
#include <string>
#include <string.h>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <stdio.h>
#include <math.h>
using namespace std;
map<string, int> name;
int m_like[7][7];
int score[3];
int man[7];
int min_dif, max_val;
void ready()
{
name["Anka"] = 0;
name["Chapay"] = 1;
name["Cleo"] = 2;
name["Troll"] = 3;
name["Dracul"] = 4;
name["Snowy"] = 5;
name["Hexadecimal"] = 6;
memset(m_like, 0, sizeof(m_like));
min_dif = INT_MAX;
max_val = 0;
}
void dfs(int beg)
{
if(beg == 7)
{
int num[3] = {0};
for(int i = 0; i < 7; i++)
num[man[i]]++;
for(int i = 0; i < 3; i++)
if(num[i] == 0) return;
int m_dif = 0;
for(int i = 0; i < 3; i++) for(int j = 0; j < 3; j++)
{
int a = int(score[i] / num[i]);
int b = int(score[j] / num[j]);
if(abs(a - b) > m_dif)
m_dif = abs(a - b);
}
int m_val = 0;
for(int i = 0; i < 7; i++) for(int j = 0; j < 7; j++)
{
if(m_like[i][j] && man[i] == man[j])
m_val++;
}
//printf("d: %d %d\n", m_dif, m_val);
if(m_dif < min_dif)
{
min_dif = m_dif;
max_val = m_val;
}
else if(m_dif == min_dif && m_val > max_val)
{
max_val = m_val;
}
return;
}
for(int i = 0; i < 3; i++)
{
man[beg] = i;
dfs(beg + 1);
}
}
int main()
{
ready();
int n;
scanf("%d", &n);
while(n--)
{
string a, like, b;
cin >> a >> like >> b;
m_like[name[a]][name[b]] = 1;
}
scanf("%d%d%d", &score[0], &score[1], &score[2]);
/*
for(int i = 0; i < 7; i++)
{
for(int j = 0; j < 7; j++)
printf("%d ", m_like[i][j]);
printf("\n");
}
*/
dfs(0);
printf("%d %d\n", min_dif, max_val);
}
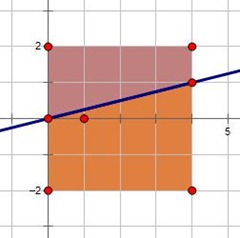
p, q是实数,p会取[0, a]中的任意值,q的范围是[-b, b],为使x^2+sqrt(p)*x+q=0至少有一个根的(p,q)取法概率是多少。
要使Delta>=0,即p-4q>=0,然后p,q的取值形成一个矩形,然后就可以求概率了,注意p=0,q=0的情况,当时晕晕的,想起来真恶心,三角形面积忘除以2等等,具体的看下图就明白了。
#include <iostream>
#include <string>
#include <string.h>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <stdio.h>
#include <math.h>
using namespace std;
double go(double p, double q)
{
double q1 = p / 4;
double p1 = q * 4;
if(q1 <= q) return (p * q1 + p * q * 2) / (4 * p * q);
else return 1 - (q * p1 / 2) / (2 * p * q);
}
int main()
{
/*
for(int i = 1; i <= 10; i++)
{
for(int j = 1; j <= 10; j++)
printf("%.6lf ", go(i, j));
printf("\n");
}
*/
int T;
scanf("%d", &T);
while(T--)
{
double one = 1;
double zero = 0;
int p, q;
scanf("%d%d", &p, &q);
if(q == 0 && p == 0) printf("%.10lf\n", one);
else if(q == 0 && p != 0) printf("%.10lf\n", one);
else if(p == 0 && q != 0) printf("0.5\n");
else printf("%.10lf\n", go(p, q));
}
}
这题比较有意思,给一颗树,N个节点(N<=10^5),给定一个起点S,每个节点上有个参数记做Val(u),表示节点u上有Val(u)个果子,然后从S开始移动,假设一个移动从S->T,则T上的果子少掉一个(被吃掉了),如果T处没有果子,是不可以移动到这里的,然后问说从S开始移动,最多可以吃掉多少个果子。
这题的解法有点贪心的思想,想这题的时候,感觉很混乱,因为可以吃来吃去的,显得很无序,看了solution之后,把这些无序的过程整理的十分有序,并且很好的解决了这个问题,对于从一个地方吃到两一个地方,然后再吃回去,其实可以通过上面的过程去统一的,也就是可以递归下去,有子问题这个性质(这里不能给出严谨的说明),对于当前节点u,下面的儿子记做v1,v2,v3…vn,dfs(u)记做以u为父节点的子树,吃完后返回u吃的做多的果子数,同时记录下left(u)表示吃完最多后剩下的果子数,求dfs(u)的过程是,先对u的儿子儿子全部求一遍dfs,然后把儿子的最大果子数排一下序,从大到小开始吃,如果吃完后u处还有剩下果子,就对儿子的余下的果子,依次吃,这时只能吃儿子的根,因为如果能往下再吃的话,那么刚才就吃掉了,当然这里不能模拟,求下min(left(u), left(vi))就可以了,最后的复杂度是O(NlogN)。
#include <iostream>
#include <string>
#include <string.h>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <stdio.h>
#include <math.h>
using namespace std;
const int MAX = 100005;
typedef __int64 int64;
vector<int> tree[MAX];
int n, val[MAX];
void dfs(int f, int u, int64& max_get, int& left)
{
vector<int> v_left;
vector<int64> v_get;
for(int i = 0; i < tree[u].size(); i++)
{
int v = tree[u][i];
if(v != f && val[v]) //val[v]要有值才可达
{
int c_left = val[v] - 1;
int64 c_get;
dfs(u, v, c_get, c_left);
v_get.push_back(c_get);
v_left.push_back(c_left);
}
}
sort(v_get.begin(), v_get.end());
max_get = 0;
for(int i = v_get.size() - 1; left && i >= 0; i--)
{
left--;
max_get += v_get[i] + 2;
}
for(int i = 0; i < v_left.size() && left; i++)
{
int t = min(left, v_left[i]);
left -= t;
max_get += 2 * t;
}
//printf("%d get %I64d left %d\n", u, max_get, left);
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d", &val[i]);
for(int i = 1; i < n; i++)
{
int a, b;
scanf("%d%d", &a, &b);
tree[a].push_back(b);
tree[b].push_back(a);
}
int root;
scanf("%d", &root);
int64 ans;
dfs(0, root, ans, val[root]);
printf("%I64d\n", ans);
}
问题是有个N*M的矩阵,要对它进行1*2的子集完全划分,有一定的规则可以使得两个元素放在一起,然后求合理的方法数,最后模1e9+7。
不得不说,题目读的很痛苦,怪自己英语没到家,大牛们都读的很快。因为这题有个特别的限制,就是如果有一个1*2的划分,那么这N*2列的元素中不能有其他的1*2的小方块,横着插进来,然后这题就可以用DP做了。
Dj = Dj-2 * Pj-1 + Dj-1 * Qj - Dj-2 * Qj-1 * Qj, D0=1, D1=Q1,Dj表示前j列的合法数,Pj表示第j和第j+1列这两列的合法数,Qj表示第j列的合法数(0 or 1)。
其实,前j列的排列数,可以按最后两列的情况来划分,一个是最后两列中有横着的,一个是最后两列中没有横着的,后者好处理,通过Dj-1来转移,前者直接处理不好处理,因此先求Pj-1,然后会有全部都是竖着的情况是和前者重复的,要减去,因此有了转移方程中的第三项。对于P,Q按着行,从上往下DP下就可以求出了。
#include <iostream>
#include <string>
#include <string.h>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <stdio.h>
#include <math.h>
using namespace std;
const int MAX = 255;
const int M = 1e9 + 7;
typedef __int64 int64;
int n, m, domi[MAX][MAX];
int64 P[MAX][MAX], Q[MAX][MAX];
int64 D[MAX];
char mm[5 * MAX][5 * MAX];
void Read()
{
scanf("%d%d", &n, &m);
for(int i = 0; i < 4 * n + 1; i++)
scanf("%s", mm[i]);
}
int CanX(int a, int b)
{
if(a != 2 && a != 3 && a != 6 &&
b != 2 && b != 3 && b != 6)
return 1;
else return 0;
}
int CanY(int a, int b)
{
if(a < 7 && b < 7) return 1;
else return 0;
}
void Pre()
{
//domi
for(int i = 0; i < n; i++) for(int j = 0; j < m; j++)
{
int bi = 4 * i + 1;
int bj = 4 * j + 1;
int p_num = 0;
for(int di = 0; di < 3; di++) for(int dj = 0; dj < 3; dj++)
{
if(mm[bi + di][bj + dj] == 'O') p_num++;
}
if(p_num == 2 && mm[bi][bj] == 'O') p_num += 7;
else if(p_num == 3 && mm[bi][bj] == 'O') p_num += 7;
else if(p_num == 6 && mm[bi][bj + 1] == 'O') p_num += 7;
domi[i + 1][j + 1] = p_num;
}
/*
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
printf("%d ", domi[i][j]);
printf("\n");
}
*/
//Q
for(int j = 1; j <= m; j++)
{
Q[0][j] = 1;
Q[1][j] = 0;
for(int i = 2; i <= n; i++)
Q[i][j] = Q[i - 2][j] * CanY(domi[i][j], domi[i - 1][j]);
}
//P
for(int j = 1; j < m; j++)
{
P[0][j] = 1;
P[1][j] = CanX(domi[1][j], domi[1][j + 1]);
for(int i = 2; i <= n; i++)
{
P[i][j] = ( P[i - 1][j] * CanX(domi[i][j], domi[i][j + 1]) +
P[i - 2][j] * CanY(domi[i - 1][j], domi[i][j]) *
CanY(domi[i - 1][j + 1], domi[i][j + 1]) ) % M;
}
}
}
void Solve()
{
D[0] = 1;
D[1] = Q[n][1];
for(int j = 2; j <= m; j++)
{
D[j] = ( D[j - 2] * P[n][j - 1] +
D[j - 1] * Q[n][j] -
D[j - 2] * Q[n][j - 1] * Q[n][j] ) % M;
}
printf("%I64d\n", (D[m] + M) % M);
}
int main()
{
Read();
Pre();
Solve();
}
E. Martian Food
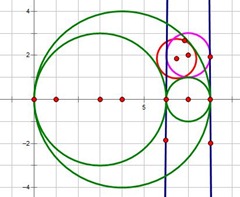
这是个经典问题,The Shoemaker's Knife。
这道几何题考的比较偏僻,但是很有意思,让人学到了不少的东西,认识到了广义圆等等,通过另一篇随笔进行详细的介绍。这里大致讲下思路,用到了反演几何的知识,圆和直线有相似的特性,这里的圆的反演类比与点关于直线的对称,这样子,直线和圆反演后就变成直线和圆了,然后关于圆的位置关系等,就可以通过反演后方便的得到了,当然这要靠它的特性了,下图中,两个半径为r,R的圆反演成直线,然后要求的圆在两条直线的中间,然后求的第K个圆的位置后,再反演回来就行,关于反演可以通过极角坐标系很好的解释下变换,角度没变,半径求倒数。
#include <iostream>
#include <string>
#include <string.h>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <stdio.h>
#include <math.h>
using namespace std;
int main()
{
int t;
scanf("%d", &t);
while(t--)
{
double R, r;
int k;
scanf("%lf%lf%d", &R, &r, &k);
double A = 1 / (2 * R);
double B = 1 / (2 * r);
double ox = (A + B) / 2;
double oy = k * (B - A);
double or = (B - A) / 2;
double ok = sqrt(ox * ox + oy * oy);
double ans = (1 / (ok - or) - 1 / (ok + or)) / 2;
printf("%.8lf\n", ans);
}
}