什么是NumPy?
NumPy是Python中科学计算的基本软件包。它是一个Python库,提供多维数组对象,各种派生对象(例如蒙版数组和矩阵)
以及各种例程,用于对数组进行快速操作,包括数学,逻辑,形状处理,排序,选择,I / O ,离散傅立叶变换,基本线性代数,基本统计运算,随机模拟等等。
NumPy包的核心是ndarray对象。这封装了均匀数据类型的n维数组,为了提高性能,许多操作都在编译后的代码中执行。NumPy数组和标准Python序列之间有几个重要的区别:
- NumPy数组在创建时具有固定的大小,这与Python列表(可以动态增长)不同。更改ndarray的大小将创建一个新数组并删除原始数组。
- NumPy数组中的所有元素都必须具有相同的数据类型,因此在内存中的大小将相同。例外:一个对象可以具有(Python,包括NumPy)对象的数组,从而允许数组具有不同大小的元素。
- NumPy数组有助于对大量数据进行高级数学运算和其他类型的运算。通常,与使用Python的内置序列相比,此类操作可以更高效地执行,并且代码更少。
- 越来越多的基于Python的科学和数学软件包都使用NumPy数组。尽管这些通常支持Python序列输入,但它们会在处理之前将此类输入转换为NumPy数组,并且通常会输出NumPy数组。换句话说,为了有效地使用很多(也许甚至是大多数)当今基于科学/数学的基于Python的软件,仅仅知道如何使用Python的内置序列类型是不够的-人们还需要知道如何使用NumPy数组。
- (总结就是一个在Python中做科学计算的基础库,重在数值计算,也是大部分PYTHON科学计算库的基础库,多用于在大型、多维数组上执行数值运算)
为什么NumPy快速?
向量化描述了代码中没有任何显式的循环,索引等操作-当然,这些事情发生在优化的预编译C代码中的“幕后”。向量化代码具有许多优点,其中包括:
- 向量化的代码更简洁,更易于阅读
- 更少的代码行通常意味着更少的错误
- 该代码更类似于标准数学符号(通常更容易正确地编码数学结构)
- 向量化产生更多的“ Pythonic”代码。没有向量化,我们的代码将效率低下且难以读取
for循环。
广播是一个术语,用于描述操作的隐式逐元素行为。一般而言,在NumPy中,所有运算,不仅是算术运算,而且是逻辑,按位,函数等,均以这种逐个元素的隐式方式进行操作,即广播。而且,在上面的示例中,
a并且b可以是相同形状的多维数组,或者是标量和数组,甚至可以是形状不同的两个数组,条件是较小的数组可以“扩展”到较大的形状。最终广播是明确的。有关广播的详细“规则”,请参见numpy.doc.broadcasting。还有谁使用NumPy?
NumPy完全支持面向对象的方法,再次从ndarray开始。例如,ndarray是一个类,具有许多方法和属性。它的许多方法都由最外层的NumPy命名空间中的函数反映,从而允许程序员以他们喜欢的任何范式进行编码。这种灵活性使NumPy数组方言和NumPy ndarray类成为了Python中使用的多维数据交换的事实上的语言。
特点:快速、方便、科学计算库
numpy创建数组(矩阵)
import numpy as np #创建数组 a = np.array([1,2,3,4,5]) b = np.array(range(1,6)) c = np.arange(1,6)#b和c相比,方便 print(a,b,a) #上面创建a,b,c都相同,都是创建了一个一维数组
数组的类名
a = np.array([2,3,4,5,6]) print(type(a))
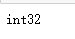
数组的类型
print(a.dtype)
数据类型的操作
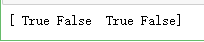
指定创建的数组的数据类型
# a = np.array([1,0,2,0],dtype=np.bool)#或者使用dtype="?" a = np.array([1,0,2,0],dtype="?")#或者使用dtype="?" print(a)
修改数组的数据类型
# a.astype("i1")#或者使用a.astype(np.int8) a.astype(np.int8)
修改浮点型的小数位数
import random #生成一维10个数的数组 a = np.array([random.random() for i in range(10)]) print(a) print(type(a)) print(a.dtype)
#保留几位小数 b = np.round(a,2) print(b)
数组的形状
a = np.array([[1,2,3,4,5],[6,7,8,9,10]]) a
查看数组的形状
b = a.reshape(5,2) print(b) print(a)#可以看出修改形状,不是在a的基础上修改 #是备份修改的
把数组转化为1维数据
c = b.reshape(1,10)##注意这不是一维数组,这是二维 print("c",c) d = b.reshape((10,)) print("d",d)#这才是一维数组 注意看中括号 b.flatten()#这个是一维的 b.reshape(1,10)#这个是二维的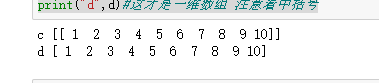


数组和数的计算

有趣吧,这是一个numpy的广播机制造成的,在运算过程中,加减乘除的值被广播到所有的元素上面(有点像计算机网络同一个局域网中广播机制)
数组和数组的计算(我将jupyter notebook中练习直接截图出来)
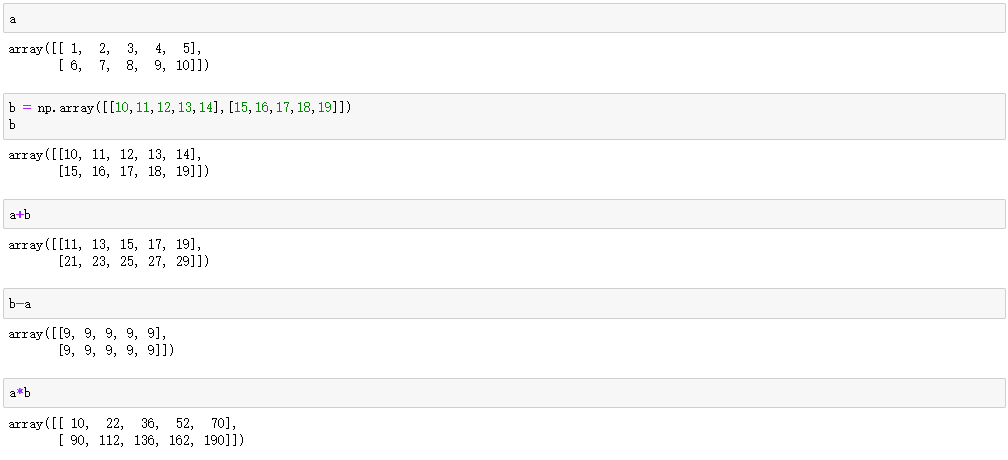
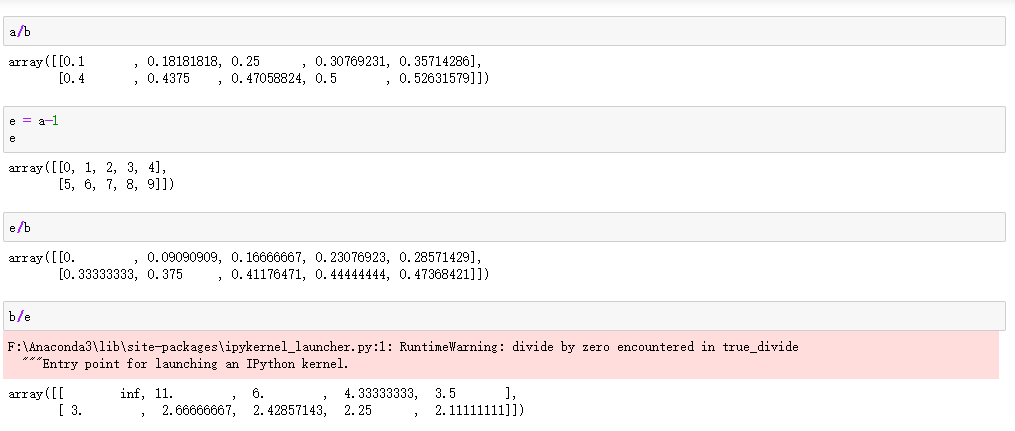

在上面可以看出结果中有inf这个标志,这是无穷大的意思,是无穷大单词的缩写。
不同维度的数组计算:
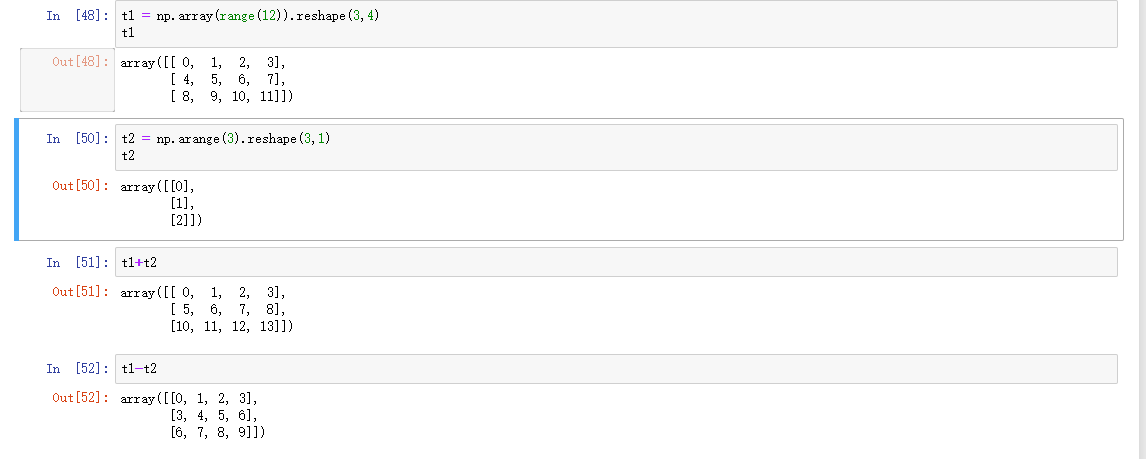
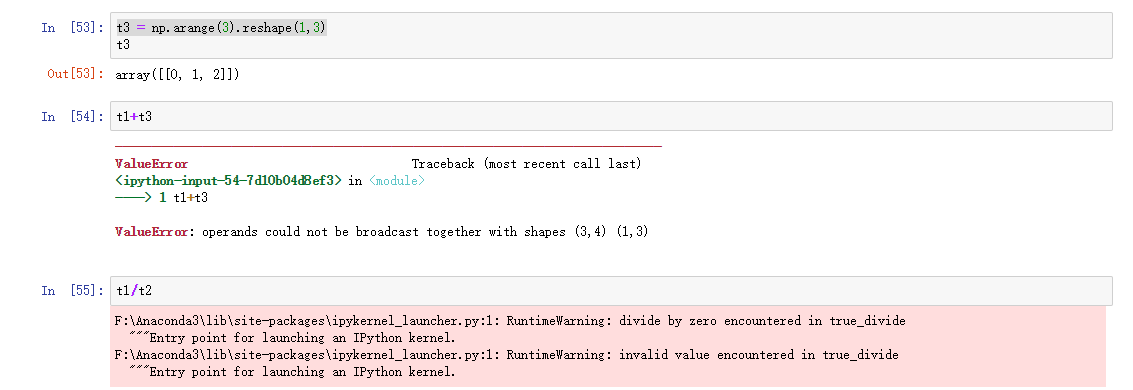

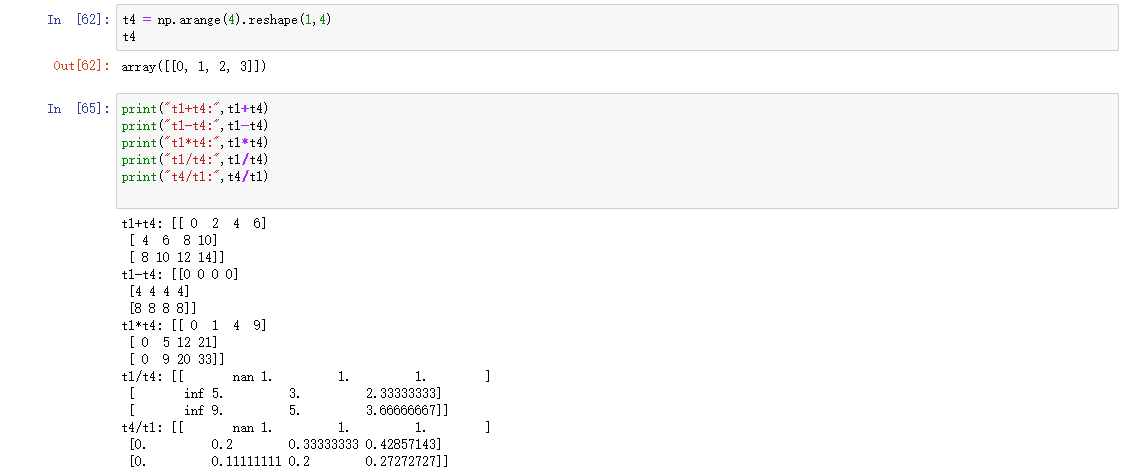
总结:上面(ValueError: operands could not be broadcast together with shapes (3,4) (1,3))这个错误是由于数组t1与t3在任一维度没有相等的,
所以不能进行运算。无论多维,只要存在一个维度相当,即可参与运算。
广播原则(重要)
- 如果两个数组的后缘维度(trailing dimension,即从末尾开始算起的维度)的轴长度相符或其中一方的长度为1,则认为它们是广播兼容的。广播会在缺失和(或)长度为1的维度上进行。
怎么理解呢? 可以把维度指的是shape所对应的数字个数那么问题来了: shape为(3,3,3)的数组能够和(3,2)的数组进行计算么?
答案是不能的,在任意维度没有相同的,是不能进行运算的。
shape为(3,3,2)的数组能够和(3,2)的数组进行计算么? 有什么好处呢?
可以进行运算,存在维度相同,换句话来说理解有点难,那么可以想出一维与二维进行运算的条件也就是这个意思。
举个例子:每列的数据减去列的平均值的结果
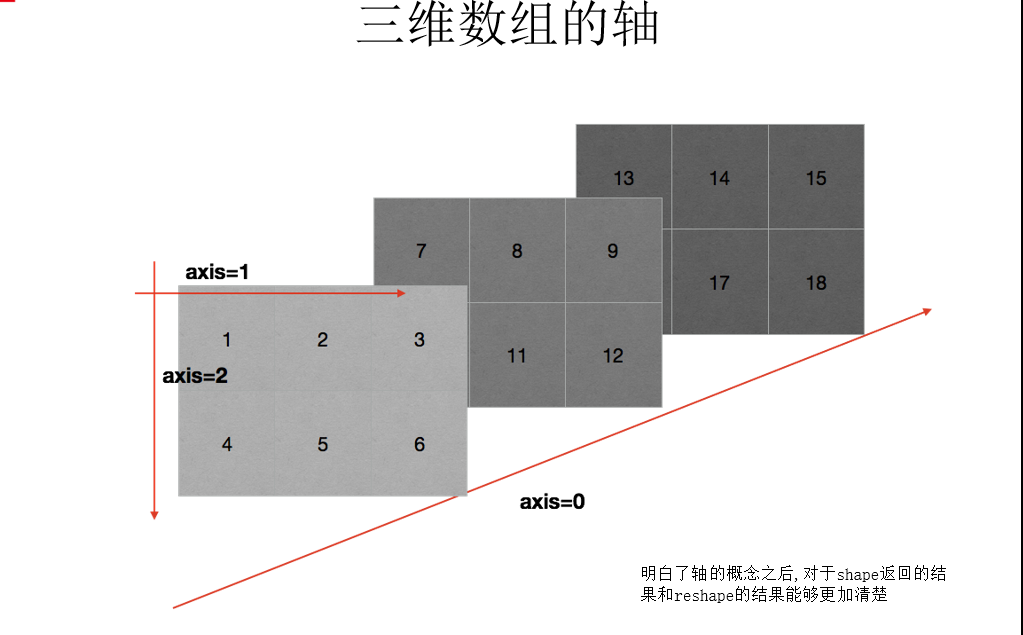
轴(axis)
在numpy中可以理解为方向,使用0, 1,2...数字表示,对于一个- -维数组,只有一个0轴,对于2维数组(shape (2, 2)),有0轴和1轴,对于三维数组(shape(2,2,3)), 有0, 1, 2轴 有了轴的概念之后,我们计算会更加方便,比如计算一个2维数组的平均值,必须指定是计算哪个方向上面的数字的平均值 那么问题来了: 在前面的知识,轴在哪里? 回顾np. arange (0, 10). reshape (2, 5)), reshpe中2表示0轴长度(包含数据的条数)为2, 1轴长度为5, 2*5-共10个数据二维数组的轴:
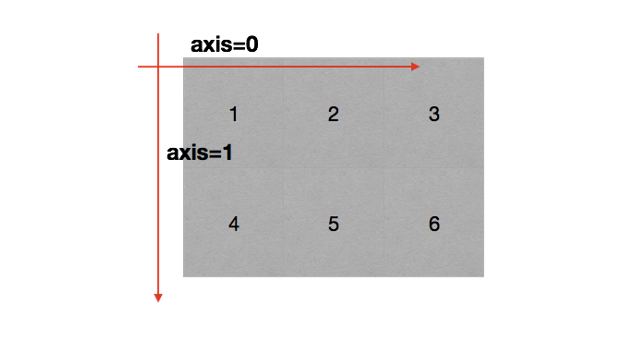
三维数组的轴: