Arcpy处理修改shapefile FeatureClass 线要素坐标

需求：在开发的webgis系统中需要将道路矢量数据与谷歌地图瓦片叠加，谷歌地图瓦片在国家测绘局的要求是进行了偏移处理的，人称“火星坐标系GCJ_02”，道路数据是WGS-84坐标系下的经纬度坐标，现在知道WGS-84向GCJ_02转换的公式，需要对道路矢量数据进行坐标转换和偏移的批处理。

简要描述： 处理shapefile线要素，修改每个点的坐标。

参考资料：

1. 关于坐标转换计算： 在另一篇文章中有参考资料 http://www.cnblogs.com/beautifulplanet/p/4309222.html

2. 如何用arcpy进行处理呢，先找到这个链接

http://gis.stackexchange.com/questions/17096/edit-end-points-in-polyline-python-arcmap10，

从def offsetFirstPointInLine(line_geom,X_distance,Y_distance)函数中找到如何提取每一条线记录的每个点坐标：

geom = r.getValue("SHAPE")
array = geom.getPart(0)

那array 是什么呢？

可以通过打印array.count，并使用ArcToolBox中的Data Interoperability Tools -> Quick Export ，将需要处理的数据导出为Geojson格式的文件，然后对比一下array.count的值和Geojson文本中的数据，再进行打印：

for x in range(1,array.count):

   print array[x].X

   print array[x].Y

应该就知道怎么定位到点了吧~

3. 上面那个例子只处理了每条线的一个点，而我需要对每个点进行处理，那怎么构成其中的new line呢？又去找ArcGIS的帮助，找到PolyLine类

http://help.arcgis.com/zh-cn/arcgisdesktop/10.0/help/index.html#/na/000v000000n2000000/

看看其中polyline是如何由点组装起来的。

解决方案：

经过上面三步梳理，整理代码如下

>>> import arcpy,math
... pi = 3.14159265358979324
... a = 6378245.0
... ee = 0.00669342162296594323
... def transformLat(x,y):
...     ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y + 0.2 * math.sqrt(abs(x))
...     ret += (20.0 * math.sin(6.0 * x * pi) + 20.0 * math.sin(2.0 * x * pi)) * 2.0 / 3.0
...     ret += (20.0 * math.sin(y * pi) + 40.0 * math.sin(y / 3.0 * pi)) * 2.0 / 3.0
...     ret += (160.0 * math.sin(y / 12.0 * pi) + 320 * math.sin(y * pi / 30.0)) * 2.0 / 3.0
...     return ret 
... def transformLon(x,y):
...     ret = 300.0 + x + 2.0 * y + 0.1 * x * x + 0.1 * x * y + 0.1 * math.sqrt(abs(x))
...     ret += (20.0 * math.sin(6.0 * x * pi) + 20.0 * math.sin(2.0 * x * pi)) * 2.0 / 3.0
...     ret += (20.0 * math.sin(x * pi) + 40.0 * math.sin(x / 3.0 * pi)) * 2.0 / 3.0
...     ret += (150.0 * math.sin(x / 12.0 * pi) + 300.0 * math.sin(x / 30.0 * pi)) * 2.0 / 3.0
...     return ret 
... def offsetPoint(wgLat,wgLon):
...     dLat = transformLat(wgLon - 105.0, wgLat - 35.0)
...     dLon = transformLon(wgLon - 105.0, wgLat - 35.0)
...     radLat = wgLat / 180.0 * pi
...     magic = math.sin(radLat)
...     magic = 1 - ee * magic * magic
...     sqrtMagic = math.sqrt(magic);
...     dLat = (dLat * 180.0) / ((a * (1 - ee)) / (magic * sqrtMagic) * pi)
...     dLon = (dLon * 180.0) / (a / sqrtMagic * math.cos(radLat) * pi)
...     new_point = arcpy.Point(wgLon+dLon, wgLat+dLat)
...     return new_point
... def offsetFirstPointInLine(line_geom):
...     new_point = arcpy.Point()
...     new_array = arcpy.Array()
...     array = line_geom.getPart(0)
...     for x in range(0,array.count):
...         old_point = array[x]
...         new_point = offsetPoint(old_point.Y,old_point.X)
...         new_array.add(new_point)
...     new_line = arcpy.Polyline(new_array,SR)   
...     new_array.removeAll()
...     return new_line
... fc = r"E:movedata-lonlatguodao.shp"    
... cur= arcpy.UpdateCursor(fc)
... SR= arcpy.Describe(fc).spatialReference
... print SR
... for r in cur:
...     geom = r.getValue("SHAPE")
...     r.setValue("SHAPE",offsetFirstPointInLine(geom))
...     cur.updateRow(r)
... del r,cur

将处理后的数据再进行Project ： WGS 1984 Web Mercator.prj，与谷歌地图进行叠加显示位置一致。

有几句代码标红，是遇到数据缺失的问题后修改的，过程如下：

遇到的问题：

但是...后来放大数据，才发现有缺失，如图（紫色是原始数据，红色是处理后得到的数据）

数据缺失问题解决尝试：

new_array.add(new_point)
new_line = arcpy.Polyline(new_array)
打印new_array也是38个点，但是打印new_line.pointCount就只有3个点了。

重新分析测试数据（WGS-84 地理坐标系/经纬度 下进行），启用编辑状态，原始的线要素上点比较密集

用 Arcpy Polyline lose points 去谷歌 搜到 http://stackoverflow.com/questions/14248618/shape-information-lost-when-using-arcpy-polyline-object-as-dictionary-value

好像是要添加坐标系，另外又进行了实验：

给这条线加上几个点，其中有几个点距离比较近：

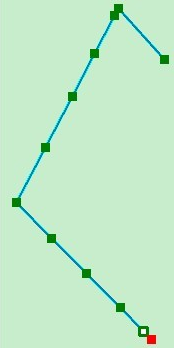
再次处理，线变成了：

推测是不是在构成线的时候有什么距离限制？

用ArcPy Polyline accuracy、 ArcPy Polyline tolerance 谷歌，搜到了http://gis.stackexchange.com/questions/86728/minimum-shapelength-using-arcpy-polyline

其中关键的一句 “ I recommend setting the Geometry's Spatial Reference before inputting the coordinates. The SR has its own XYTolerance and XYResolution” 

因此对上面的程序进行修改，增加红色部分。