前面介绍了前序线索化二叉树、中序线索化二叉树,本文将介绍后序线索化二叉树。之所以用单独的一篇文章来分析后序线索化二叉树,是因为后序线索化二叉树比前序、中序要复杂一些;另外在复习线索化二叉树的过程中,大部分讲解数据结构的书籍中都是以中序线索化为例,在网上搜索也很少有详细讲解前序、后序线索化的文章,对于使用Java语言编写的代码更是凤毛麟角,因此决定把个人的理解过程记录下,并分享给有需要的同学参考。
一、图解后序线索化
如果你很清楚的理解了前序、中序线索化二叉树,那么下面的图解不难理解;如果你还未掌握前序、中序线索化二叉树,请先详细了解线索二叉树之前序、中序线索化,然后再回来阅读本文更便于理解。
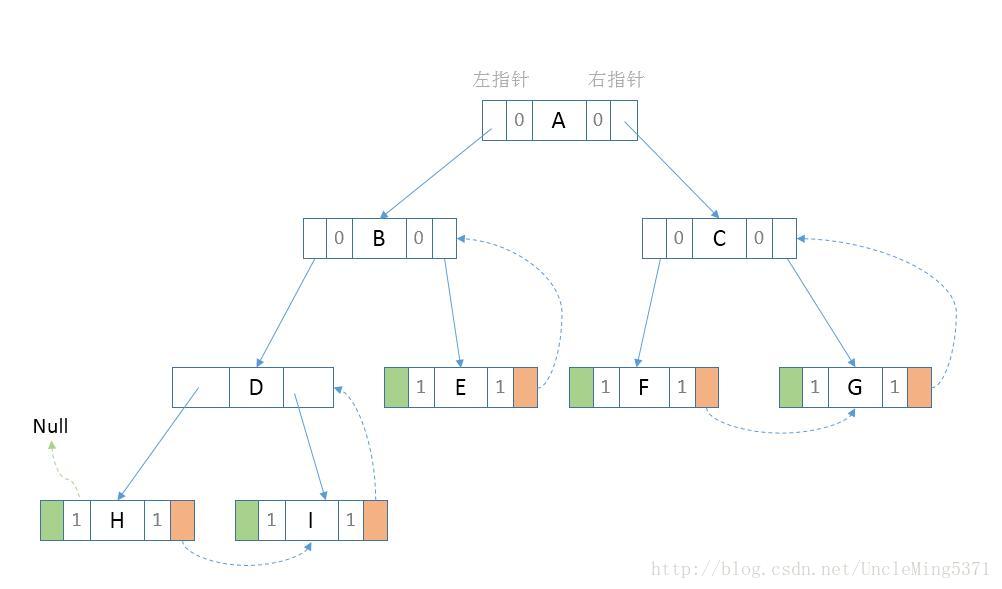
下图是一棵后序线索化的二叉树,如下图:
为了更清晰、直观的表示出后继线索,在上图中忽略了前驱线索,请自行脑补。通过观察上图,节点H的后继节点是I,因此节点H的right指针指向I;节点I的后继节点是D,因此节点D的right指针指向D;节点D的后继节点是E,但是节点D的right指针指向了子节点B,因此D的right指针也就不能指向后继节点;同理节点B也没办法指向后继节点F。
对这棵二叉树完成后序线索化之后,我们在对其进行遍历时,我们知道后序遍历的顺序是:左右根,那对于上图的后序遍历结果是:HIDEBFGCA。
遍历后序线索化二叉树的思路:由于是后序线索化,那么后序遍历的开始节点一定是最左子节点,从根节点出发找到最左子节点,如何判断是否是最左子节点呢?如果是最左子节点,则其left指针一定的线索,如上图我们找到最左子节点H,H的right指针是后继线索,找到节点I,节点I的right指针是后继线索,找到节点D,节点D的right指针是子节点I,并不是后继线索指针,那么问题来了?此时我们该如何处理呢?
通过观察D的后继节点E,但是D与E没有直接线索,不过D的父节点是B,B的右字节是E,存在这样一个间接的关系,我们是否可以利用这个间接的关系呢?答案是肯定的,但是按照我们上文介绍的节点数据结构,并不存在指向父节点的指针,因此我们要对节点数据结构进行修改,修改如下:
//节点存储结构
static class Node {
String data; //数据域
Node left; //左指针域
Node right; //右指针域
Node parent; //父节点的指针(为了后序线索化使用)
boolean isLeftThread = false; //左指针域类型 false:指向子节点、true:前驱或后继线索
boolean isRightThread = false; //右指针域类型 false:指向子节点、true:前驱或后继线索
Node(String data) {
this.data = data;
}
}按照如上的存储结构增加了parent指针之后,D节点存在了指向父节点B的指针。当遍历到D节点时找到D节点的父节点B,B的right指针指向了子节点E,E的right指针又指向了B,这里又出现了另一个问题,就是进入了两次B,如果按照前面的方式则进入了一个死循环。以节点B为例,我们什么时候去找B的父节点,什么时候去处理他的右节点呢。我们分析下两次进入节点B,第一次是通过B的左节点进入,第二次是通过右子节点进入,我们可以记录上一个处理的节点,如果上一个处理的节点是B的左节点,则接下进入B的右节点,如果上一个处理的节点是B的右节点,则说明B的左右子树都处理完成,继续处理B的父节点。
二、Java代码实现后序线索化
package com.bj58.demo.struct;
/**
* @Title: 后序线索化二叉树相关操作
* @Description:
* @Author: Uncle Ming
* @Date:2017年1月8日 下午3:42:14
* @Version V1.0
*/
public class PostThreadBinaryTree {
private Node preNode; //线索化时记录前一个节点
//节点存储结构
static class Node {
String data; //数据域
Node left; //左指针域
Node right; //右指针域
Node parent; //父节点的指针(为了后序线索化使用)
boolean isLeftThread = false; //左指针域类型 false:指向子节点、true:前驱或后继线索
boolean isRightThread = false; //右指针域类型 false:指向子节点、true:前驱或后继线索
Node(String data) {
this.data = data;
}
}
/**
* 通过数组构造一个二叉树(完全二叉树)
* @param array
* @param index
* @return
*/
static Node createBinaryTree(String[] array, int index) {
Node node = null;
if(index < array.length) {
node = new Node(array[index]);
node.left = createBinaryTree(array, index * 2 + 1);
node.right = createBinaryTree(array, index * 2 + 2);
//记录节点的父节点(后序线索化遍历时使用)
if(node.left != null) {
node.left.parent = node;
}
if(node.right != null) {
node.right.parent = node;
}
}
return node;
}
/**
* 后序线索化二叉树
* @param node 节点
*/
void postThreadOrder(Node node) {
if(node == null) {
return;
}
//处理左子树
postThreadOrder(node.left);
//处理右子树
postThreadOrder(node.right);
//左指针为空,将左指针指向前驱节点
if(node.left == null) {
node.left = preNode;
node.isLeftThread = true;
}
//前一个节点的后继节点指向当前节点
if(preNode != null && preNode.right == null) {
preNode.right = node;
preNode.isRightThread = true;
}
preNode = node;
}
/**
* 后续遍历线索二叉树,按照后继方式遍历(思路:后序遍历开始节点是最左节点)
* @param node
*/
void postThreadList(Node root) {
//1、找后序遍历方式开始的节点
Node node = root;
while(node != null && !node.isLeftThread) {
node = node.left;
}
Node preNode = null;
while(node != null) {
//右节点是线索
if(node.isRightThread) {
System.out.print(node.data + ", ");
preNode = node;
node = node.right;
} else {
//如果上个处理的节点是当前节点的右节点
if(node.right == preNode) {
System.out.print(node.data + ", ");
if(node == root) {
return;
}
preNode = node;
node = node.parent;
} else { //如果从左节点的进入则找到有子树的最左节点
node = node.right;
while(node != null && !node.isLeftThread) {
node = node.left;
}
}
}
}
}
public static void main(String[] args) {
String[] array = {"A", "B", "C", "D", "E", "F", "G", "H", "I"};
Node root = createBinaryTree(array, 0);
PostThreadBinaryTree tree = new PostThreadBinaryTree();
tree.postThreadOrder(root);
System.out.println("后序按后继节点遍历线索二叉树结果:");
tree.postThreadList(root);
}
}
运行结果如下:
后序按后继节点遍历线索二叉树结果:
H, I, D, E, B, F, G, C, A,
三、前序、中序、后序线索化比较
1. 前序线索化二叉树遍历相对最容易理解,实现起来也比较简单。由于前序遍历的顺序是:根左右,所以从根节点开始,沿着左子树进行处理,当子节点的left指针类型是线索时,说明到了最左子节点,然后处理子节点的right指针指向的节点,可能是右子树,也可能是后继节点,无论是哪种类型继续按照上面的方式(先沿着左子树处理,找到子树的最左子节点,然后处理right指针指向),以此类推,直到节点的right指针为空,说明是最后一个,遍历完成。
2. 中序线索化二叉树的网上相关介绍最多。中序遍历的顺序是:左根右,因此第一个节点一定是最左子节点,先找到最左子节点,依次沿着right指针指向进行处理(无论是指向子节点还是指向后继节点),直到节点的right指针为空,说明是最后一个,遍历完成。
3. 后序遍历线索化二叉树最为复杂,通用的二叉树数节点存储结构不能够满足后序线索化,因此我们扩展了节点的数据结构,增加了父节点的指针。后序的遍历顺序是:左右根,先找到最左子节点,沿着right后继指针处理,当right不是后继指针时,并且上一个处理节点是当前节点的右节点,则处理当前节点的右子树,遍历终止条件是:当前节点是root节点,并且上一个处理的节点是root的right节点。
转载自:https://blog.csdn.net/UncleMing5371/article/details/54291221