算法介绍
和Dijkstra算法一样,Floyd算法也是为了解决寻找给定的加权图中顶点间最短路径的算法。不同的是,Floyd可以用来解决“多源最短路径”的问题。
算法思路
算法需要引入两个二维数组ShortPathTable和Patharc。ShortPathTable表示顶点到顶点的最短路径权值和的矩阵,Patharc表示对应顶点的最小路径的前驱矩阵。在为分析任何顶点之前,ShortPathTable初始化为图的邻接矩阵。
假设图G有N个顶点,那么需要对矩阵ShortPathTable进行N次更新。
第一次更新时如果:
ShortPathTable[v][w] > ShortPathTable[v][0]+ShortPathTable[0][w]
//(ShortPathTable[v][0]+ShortPathTable[0][w]表示"v与w之间经过第1个顶点的距离")
则更新:
ShortPathTable[v][w]为ShortPathTable[v][0]+ShortPathTable[0][w]
同时因为有变化,所以Patharc矩阵对应的Patharc[v][w]和Patharc[w][v]修改为当前中转的顶点的下标0。
同理,第k次更新时:如果"ShortPathTable[v][w]的距离" > “ShortPathTable[v][k]+ShortPathTable[k][w]”,则更新ShortPathTable[v][w]为"ShortPathTable[v][k]+a[k][w]"。
循环更新N次后操作完成。
算法示例

初始化时该网图矩阵(ShortPathTable)如下:
Patharc初始化为:
程序循环第一次,即k=0时,也就是所有顶点都经过中转时,没有变化。
当k=1时,也就是说所有顶点都经过中转,此时,当v=0时,原本ShortPathTable[0][2]=5,现在由于ShortPathTable[0][1]+ShortPathTable[1][2]=4。所以使ShortPathTable[0][2]=4,同理ShortPathTable[0][3]=8,ShortPathTable[0][4]=6.当v=2, 3, 4时也修改了数据。同时在矩阵Patharc上也需要做操作。
此时ShortPathTable:
此时的Patharc:
接下来就是k=2,一直到k=8,表示针对每个顶点做中转得到的计算结果。
(最终形成的ShortPathTable和Patharc矩阵我就不画了…用markdown来画矩阵好麻烦…)
代码说明
基本定义
private final int INFINITY = 65535;
public int MAXVEX;
public int[][] Patharc;
public int[][] ShortPathTable;
//这里直接使用上图的邻接矩阵了,避免了图转矩阵的步骤
public int[][] maze = {
{0, 1, 5, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY },
{1, 0, 3, 7, 5, INFINITY, INFINITY, INFINITY, INFINITY },
{5, 3, 0, INFINITY, 1, 7, INFINITY, INFINITY, INFINITY },
{INFINITY, 7, INFINITY, 0, 2, INFINITY, 3, INFINITY, INFINITY },
{INFINITY, 5, 1, 2, 0, 3, 6, 9, INFINITY},
{INFINITY, INFINITY, 7, INFINITY, 3, 0, INFINITY, 5, INFINITY},
{INFINITY, INFINITY, INFINITY, 3, 6, INFINITY, 0, 2, 7},
{INFINITY, INFINITY,INFINITY, INFINITY, 9, 5, 2, 0, 4},
{INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, 7, 4,0}
};
实现代码
public Floyd() {
this.MAXVEX = maze.length;
ShortPathTable = maze;
Patharc = new int[MAXVEX][MAXVEX];
}
public void ShortestPath_Floyd() {
int v, w, k;
for (v = 0; v < MAXVEX; v++) {
for (w = 0; w < MAXVEX; w++) {
Patharc[v][w] = w;
}
}
//核心代码
for (k = 0; k < MAXVEX; k++) {
for (v = 0; v < MAXVEX; v++) {
for (w = 0; w < MAXVEX; w++) {
if(ShortPathTable[v][w] > (ShortPathTable[v][k] + ShortPathTable[k][w])) {
ShortPathTable[v][w] = ShortPathTable[v][k] + ShortPathTable[k][w];
Patharc[v][w] = Patharc[v][k];
}
}
}
}
/**
* 最短路径的显示
*/
for (v = 0; v < MAXVEX; v++) {
for (w = 0; w < MAXVEX; w++) {
System.out.print(v + "-" + "-" + w + " weight:" + ShortPathTable[v][w] + " ");
k = Patharc[v][w];
System.out.print("path: " + v);
while(k != w) {
System.out.print("->" + k);
k = Patharc[k][w];
}
System.out.print("->" + w + "
");
}
System.out.println();
}
}
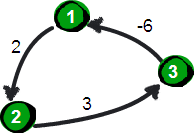
注意:弗洛伊德(Floyd)算法不能解决带有"负权回路"(又称负权环)。因为带有“负权回路”的图没有最短路。例如下面这个图就不存在1号顶点到3号顶点的最短路径。因为1->2->3->1->2->3->…->1->2->3这样路径中,每绕一次1->-2>3这样的环,最短路就会减少1,永远找不到最短路。其实如果一个图中带有“负权回路”那么这个图则没有最短路。