快速排序的理解和实现(Java)

快速排序介绍

快速排序(Quick Sort)使用分治法策略，其基本思想是：通过一趟排序将待排序记录分割成独立的两部分，其中一部分记录的关键字均比另外一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序的目的。
快排流程：

1. 从数列中选取一个基数
2. 将所有比基数小的摆放在基数前面，所有比基数大的摆在基数的后面(相同的数可以到任一边)；在这个分区退出之后，该基准就处于数列的中间位置。
3. 递归地把"基数前面的子数列"和"基数后面的子数列"进行快速排序。

举例说明：
(PS：本例参考一个大神的博客：http://www.cnblogs.com/skywang12345/p/3596746.html#a1)
数列a={30,40,60,10,20,50}为例，演示它的快速排序过程(如下图)

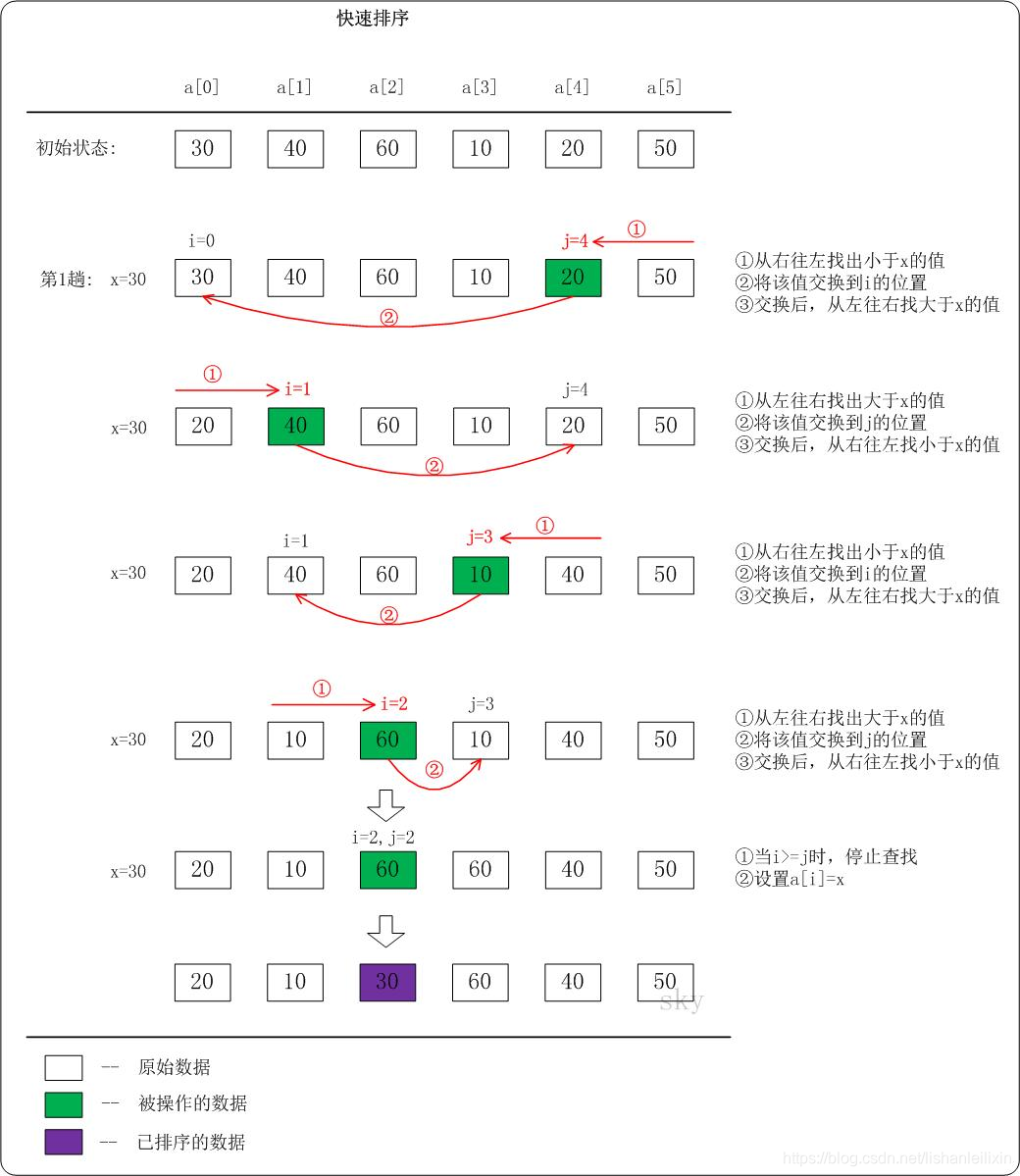
上图只是给出了第1趟快速排序的流程，按照同样的方法，对子数列进行递归遍历。最后可以得到有序序列。

代码实现：

	//对顺序表elem进行快速排序
	public void quickSort(int[] elem) {
		QSort_2(elem, 1, elem.length - 1);
	}
	
	//对顺序表elem中的子序列elem[start...end]做快速排序
	public void QSort(int[] elem, int start, int end) {
		
		int pivot;
		if(start < end) {
			pivot = Partition(elem ,start, end);
			
			QSort(elem, start, pivot - 1);
			QSort(elem, pivot + 1, end);
		}
	} 
	
	/**
	 * 交换顺序表elem中字表记录，使基数记录到位，并返回其所在位置
	 * 此时在它之前(后)的记录均不大(小)于它
	 * @param elem
	 * @param low
	 * @param high
	 * @return
	 */
	public int Partition(int[] elem, int low, int high) {
		
		int pivotkey = elem[low];

		while(low < high) {
			
			while((low < high) && (elem[high] >= pivotkey)) {
				high--;				
			}
			swap(elem, low, high);
			
			while((low < high) && (elem[low] <= pivotkey)) {
				low++;
			}
			swap(elem, low, high);
		}
		return low;
	}

快速排序复杂度分析

(PS:由于本人数学功底太弱，并没有理解快排复杂度的推演公式，在此只是摘抄于《大话数据机构》)
在最优情况下，如果排序n个关键字，其递归树的深度就是[$log_2$n] + 1（[x]表示不大于x的最大整数），即仅需要递归$log_2$n次，需要时间为T(n)的话，第一次Partiation应该是需要对整个数组扫描一遍，做n次比较。然后获得的基数将数组一分为二，那么各自还需要T($frac{n}{2}$)的时间(注意这是最好情况下，所以平分两半)。于是不断划分下去，就有下面不等式推断

T(n) ≤ 2T($frac{n}{2}$) + n, T(1)=0
T(n) ≤2(2T($frac{n}{4}$)+$frac{n}{2}$) + n=4T($frac{n}{4}$) +2n
T(n) ≤ 4(2T($frac{n}{8}$)+$frac{n}{4}$) + 2n=8T($frac{n}{8}$) +3n
…
T(n) ≤ nT(1) + ($log_2$n) * n= O(n$log$n)

也就是说在最优情况下，快排算法的时间复杂度为O(n$log$n)

在最坏情况下，待排序的序列为正序或者逆序，每次划只得到一个比上次划分少一个记录的子序列，注意另一个是空。如果画出递归树，那么就是一棵斜树。此时需要执行n-1次递归调用，且第i次划分需要经过n-i次关键字的比较才能找到第i个记录，也就是基数的位置，因此比较次数为：
$sum_{i=1}^{n-1}(n-i)=n-1+n-2+...+1= frac{n(n-1)}{2}$
最终其时间复杂度为O($n^2$)
平均情况下，设基数的关键字应该在第k的位置(1≤k≤n)，那么
$T(n)=frac{1}{n}sum_{k=1}^{n}(T(k-1) + T(n-k))+n= frac{2}{n}sum_{k=1}^{n}T(k)+n$
有数学归纳法可证明，其数量级为O(n$log$n)

就空间复杂度来说，主要是递归造成的栈空间的使用，最好情况下递归树的深度为$log_2$n，其空间复杂度也就为O($log$n)，最坏情况下，需要进行n-1次递归调用，其空间复杂度为O(n)，平均情况下，空间复杂度为O($log$n)。

由于关键字的比较和交换是跳跃式的进行，所以快速排序是一种不稳定的排序方法。

快速排序的优化

优化选取基数

采用三数取中法，即取三个关键字先进性排序，将中间数做为基数，一般是取左端，右端和中间三个数。

	//三分取中法
	public int Partition_1(int[] elem, int low, int high) {
		
		int pivotkey;

		int m = low + (high - low) / 2;
		if(elem[low] > elem[high]) {
			swap(elem, low, high);
		}
		if(elem[m] > elem[high]) {
			swap(elem, high, m);
		}
		if(elem[m] > elem[low]) {
			swap(elem, low, m);
		}
		
		pivotkey= elem[low];

		while(low < high) {
			
			while((low < high) && (elem[high] >= pivotkey)) {
				high--;				
			}
			swap(elem, low, high);
			
			while((low < high) && (elem[low] <= pivotkey)) {
				low++;
			}
			swap(elem, low, high);
		}
		return low;
	}

优化不必要的交换

	//优化不必要的交换
	public int Partition_2(int[] elem, int low, int high) {
		
		int pivotkey = elem[low];
		elem[0] = pivotkey;

		while(low < high) {
			
			while((low < high) && (elem[high] >= pivotkey)) {
				high--;				
			}
			elem[low] = elem[high];
			
			while((low < high) && (elem[low] <= pivotkey)) {
				low++;
			}
			elem[high] = elem[low];
		}
		elem[low] = elem[0];
		return low;
	}

采用替换而不是交换的方式进行操作，在性能上得到部分提升。

优化小数组时的排序

数组非常小，其快速排序不如直接插入(直插是简单排序中性能最好的)。

public final int MAX_LENGTH_INSERT_SORT = 7;

	//优化小数组时的排序方案
	public void QSort_1(int[] elem, int start, int end) {
		
		int pivot;
		if((end - start) > MAX_LENGTH_INSERT_SORT) {
			pivot = Partition(elem ,start, end);
			
			QSort(elem, start, pivot - 1);
			QSort(elem, pivot + 1, end);
		}
		else insertSort(elem);
	} 
	
	//直接插入
	public void insertSort(int[] elem) {
		int i, j;
		for (i = 2; i < elem.length; i++) {
			if(elem[i] < elem[i - 1]) {
				elem[0] = elem[i];
				for (j = i - 1; elem[j] > elem[0]; j--) {
					elem[j + 1] = elem[j];
				}
				elem[j + 1] = elem[0];
			}
		}
	}

优化递归操作

在QSort函数在其尾部有两次递归操作，若待排序序列极端不平衡，递归深度趋近于n，每次递归调用都会浪费栈空间，因此能够减少递归，将会大大提升性能。
对QSort进行尾递归操作：

	//优化递归操作
	public void QSort_2(int[] elem, int start, int end) {
		
		int pivot;
		if((end - start) > MAX_LENGTH_INSERT_SORT) {
			
			while(start < end) {
				pivot = Partition(elem ,start, end);
				QSort(elem, start, pivot - 1);
				start = pivot + 1;
			}
		}
		else insertSort(elem);
	} 

因为第一次循环后start就没了作用，可将pivot+1赋给start，再循环后，来一次Partition(elem, low, high)，其效果等同于“QSort(elem, pivot+1, end)”，结果相同，但采用迭代而不是递归可以缩减堆栈深度，从而提高性能。