数据结构与算法13—最短路径

最短路径

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。

从图中某一顶点(称为源点)到达另一顶点(称为终点)的路径可能不止一条，如何找到一条路径使得沿此路径上各边上的权值总和达到最小，例：公交查询系统。

问题解法：

求从某个源点到其余各点的最短路径 — Dijkstra算法

每一对顶点之间的最短路径 — Floyd算法

例如：

从某点到其他各顶点的最短路径

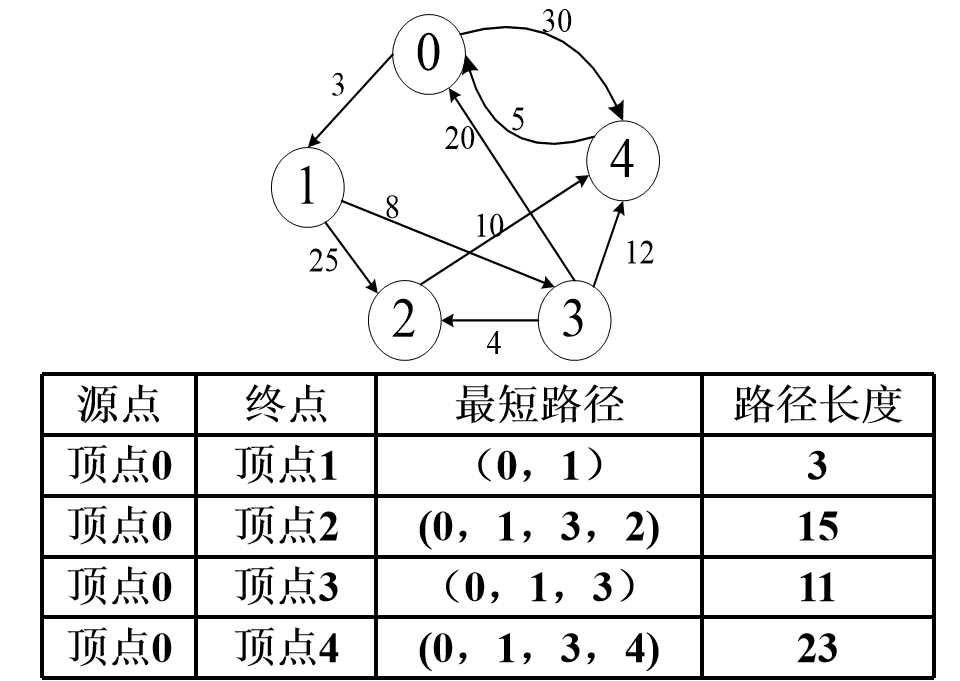
最短路径不一定是经过边最少的路径，但在这些最短路径中，长度最短的那一条路径上只有一条边，且它的权值在从源点出发的所有边的权值最小。

 路径长度最短的最短路径的特点：

在这条路径上，必定只含一条弧，并且这条弧的权值最小。

下一条路径长度次短的最短路径的特点：

它只可能有两种情况：或者是直接从源点到该点(只含一条弧)； 或者是从源点经过顶点v1，再到达该顶点(由两条弧组成)。 

迪杰斯特拉(Dijkstra)算法

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

设置辅助数组Dist，其中每个分量Dist[k]表示当前所求得的从源点到其余各顶点k的最短路径。

一般情况下，

Dist[k] = <源点到顶点k的弧上的权值> 或者 = <源点到其它顶点的路径长度>

+  <其它顶点到顶点k的弧上的权值>。

1）在所有从源点出发的弧中选取一条权值最小的弧，即为第一条最短路径。

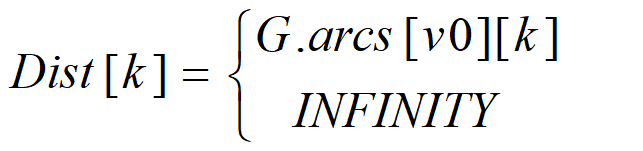
2）修改其它各顶点的Dist[k]值。 假设求得最短路径的顶点为u，

若 Dist[u]+G.arcs[u][k]<Dist[k]， 则将 Dist[k] 改为 Dist[u]+G.arcs[u][k]。

举例：求下图中从v0到其余各顶点的最短路径

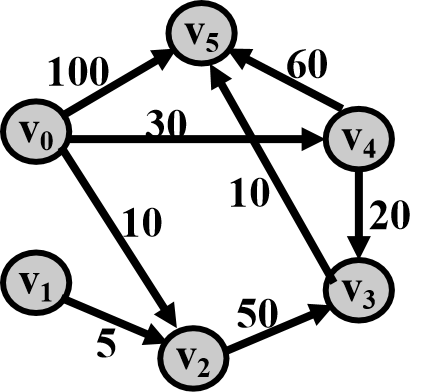
最短路径算法实现

用带权的邻接矩阵表示有向图， 对Prim算法略加改动就成了Dijkstra算法，将Prim算法中求每个顶点V_k的lowcost值用length[k]代替即可。

1. 初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

2. 从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

3. 以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

4. 重复步骤b和c直到所有顶点都包含在S中。

 Java代码实现：

以”邻接矩阵”为例对迪杰斯特拉算法进行说明

public class MatrixUDG {
    private int mEdgNum;        // 边的数量
    private char[] mVexs;       // 顶点集合
    private int[][] mMatrix;    // 邻接矩阵
    private static final int INF = Integer.MAX_VALUE;   // 最大值
    ...
}

/*
 * Dijkstra最短路径。
 * 即，统计图中"顶点vs"到其它各个顶点的最短路径。
 *
 * 参数说明：
 *       vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。
 *     prev -- 前驱顶点数组。即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。
 *     dist -- 长度数组。即，dist[i]是"顶点vs"到"顶点i"的最短路径的长度。
 */
public void dijkstra(int vs, int[] prev, int[] dist) {
    // flag[i]=true表示"顶点vs"到"顶点i"的最短路径已成功获取
    boolean[] flag = new boolean[mVexs.length];
    // 初始化
    for (int i = 0; i < mVexs.length; i++) {
        flag[i] = false;          // 顶点i的最短路径还没获取到。
        prev[i] = 0;              // 顶点i的前驱顶点为0。
        dist[i] = mMatrix[vs][i];  // 顶点i的最短路径为"顶点vs"到"顶点i"的权。
    }
    // 对"顶点vs"自身进行初始化
    flag[vs] = true;
    dist[vs] = 0;
    // 遍历mVexs.length-1次；每次找出一个顶点的最短路径。
    int k=0;
    for (int i = 1; i < mVexs.length; i++) {
        // 寻找当前最小的路径；
        // 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
        int min = INF;
        for (int j = 0; j < mVexs.length; j++) {
            if (flag[j]==false && dist[j]<min) {
                min = dist[j];
                k = j;
            }
        }
        // 标记"顶点k"为已经获取到最短路径
        flag[k] = true;
        // 修正当前最短路径和前驱顶点
        // 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
        for (int j = 0; j < mVexs.length; j++) {
            int tmp = (mMatrix[k][j]==INF ? INF : (min + mMatrix[k][j]));
            if (flag[j]==false && (tmp<dist[j]) ) {
                dist[j] = tmp;
                prev[j] = k;
            }
        }
    }
    // 打印dijkstra最短路径的结果
    System.out.printf("dijkstra(%c): 
", mVexs[vs]);
    for (int i=0; i < mVexs.length; i++)
        System.out.printf("  shortest(%c, %c)=%d
", mVexs[vs], mVexs[i], dist[i]);
}

时间复杂度：O(n²)

 弗洛伊德算法(Floyd)——求每一对顶点之间的最短路径

从任意节点i到任意节点j的最短路径不外乎2种可能：

1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

基本思想：

从vi到vj的所有可能存在的路径中，选出一条长度最短的路径。

若<vi,vj>存在，则存在路径{vi,vj};

若<vi,v1>,<v1,vj>存在，则存在路径{vi,v1,vj};

若{vi,…,v2}, {v2,…,vj}存在，则存在一条路径{vi, …, v2, …vj};

依次类推，则vi至vj的最短路径应是上述这些路径中，路径长度最小者。

具体做法为：

• 第一步，让所有边上加入中间顶点0，取A[i][j]与A[i][0]+A[0][j]中较小的值作A[i][j]的值，完成后得到A(0)
• 第二步，让所有边上加入中间顶点1，取A[i][j]与A[i][1]+A[1][j]中较小的值，完成后得到A(1)…
• 如此进行下去，当第n步完成后，得到A(n-1)，A(n-1)即为我们所求结果,A(n-1)[i][j]表示顶点i到顶点j的最短距离。

 

 Java代码实现：

以”邻接矩阵”为例对弗洛伊德算法进行说明

public class MatrixUDG {
    private int mEdgNum;        // 边的数量
    private char[] mVexs;       // 顶点集合
    private int[][] mMatrix;    // 邻接矩阵
    private static final int INF = Integer.MAX_VALUE;   // 最大值
    ...
}

/*     path -- 路径。path[i][j]=k表示，"顶点i"到"顶点j"的最短路径会经过顶点k。
 *     dist -- 长度数组。即，dist[i][j]=sum表示，"顶点i"到"顶点j"的最短路径的长度是sum。
 */
public void floyd(int[][] path, int[][] dist) {
    // 初始化
    for (int i = 0; i < mVexs.length; i++) {
        for (int j = 0; j < mVexs.length; j++) {
            dist[i][j] = mMatrix[i][j];    // "顶点i"到"顶点j"的路径长度为"i到j的权值"。
            path[i][j] = j;                // "顶点i"到"顶点j"的最短路径是经过顶点j。
        }
    }
    // 计算最短路径
    for (int k = 0; k < mVexs.length; k++) {
        for (int i = 0; i < mVexs.length; i++) {
            for (int j = 0; j < mVexs.length; j++) {
                // 如果经过下标为k顶点路径比原两点间路径更短，则更新dist[i][j]和path[i][j]
                int tmp = (dist[i][k]==INF || dist[k][j]==INF) ? INF : (dist[i][k] + dist[k][j]);
                if (dist[i][j] > tmp) {
                    // "i到j最短路径"对应的值设，为更小的一个(即经过k)
                    dist[i][j] = tmp;
                    // "i到j最短路径"对应的路径，经过k
                    path[i][j] = path[i][k];
                }
            }
        }
    }
    // 打印floyd最短路径的结果
    System.out.printf("floyd: 
");
    for (int i = 0; i < mVexs.length; i++) {
        for (int j = 0; j < mVexs.length; j++)
            System.out.printf("%2d  ", dist[i][j]);
        System.out.printf("
");
    }
}

Floyd-Warshall算法的时间复杂度为O(N³)，空间复杂度为O(N²)。