【电路图系列】模拟赛

A.电路图A

一道组合数学的题

第一个问：我们设向右转的次数为 r ，设向左转的次数为 l ，由于电流必须向顺时针旋转，所以到达时必为旋转了 2π ，所以可以得出： r=l+4 ,接下来就成了不同排列的序列个数问题，转换成计算n中选(n-4)/2个元素的组合数，使用公式Cnm=n!/(m!(n-m)!);然后下面的代码使用了费马小定理（a*a^(p-2) 同余 1 (mod p) ；所以a^(p-2)为a逆元。

第二个问：我们发现不能连续两次逆时针拐弯，不然就会形成一个不美观的凹型。所以我们把路径分成四段，可以发现每段的拐弯数都是奇数，问题转化为将 n nn 拆分成 4 个奇数的方案数（n nn 是偶数）。最终可以得到答案为：C（n/2+1,3)*n/4;

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 
 5 const int N=1e7+5,mod=1e9+7;
 6 int n,f[N];
 7 
 8 ll ksm(int a,int b){
 9     ll s=1;
10     while(b){
11         if(b&1) s=(ll)s*a%mod;
12         a=(ll)a*a%mod;
13         b>>=1;
14     }
15     return s;
16 }
17 
18 ll c(int a,int b){
19     return (ll)f[a]*ksm(f[b],mod-2)%mod*ksm(f[a-b],mod-2)%mod;
20 }
21 
22 int main(){
23     scanf("%d",&n);
24     f[0]=1;
25     for(int i=1;i<=n;i++) f[i]=(ll)f[i-1]*i%mod;
26     printf("%lld
",c(n,n/2-2));
27     printf("%lld",(ll)c(n/2+1,3)*n%mod*ksm(4,mod-2)%mod);
28     return 0;
29 }

B.电路图B

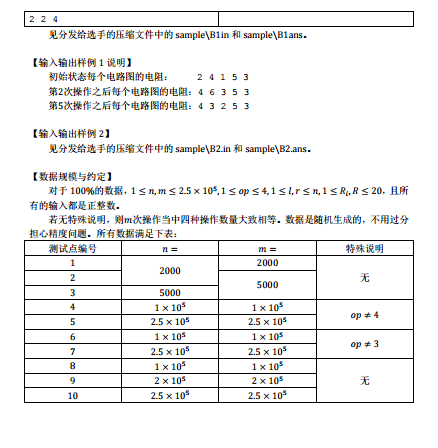
这道题很容易看出是用线段树做的（但我就是打不出来。。。qaq）

在观看了神犇李青峰(phdhd) 的代码之后，真是恍然大悟，如梦初醒，豁然开朗，豁然贯通，憬然有悟。。。。

可将一个函数{a,b,c,d}标记记为(ax+b)/(cx+d),

最关键是mix操作，将

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 #define ld long double
  4 int n,g[250010],m,op,ql,qr,md;
  5 ld ans;
  6 
  7 struct node
  8 {
  9     ld a,b,c,d,mx,mn;
 10 }s[1000010];
 11 
 12 void merge(node &x,node y)
 13 {
 14     x.mn=(x.mn*y.a+y.b)/(x.mn*y.c+y.d);
 15     x.mx=(x.mx*y.a+y.b)/(x.mx*y.c+y.d);
 16     ld a=y.a*x.a+y.b*x.c;
 17     ld b=y.a*x.b+y.b*x.d;
 18     ld c=y.c*x.a+y.d*x.c;
 19     ld d=y.c*x.b+y.d*x.d;
 20     x=(node){1,b/a,c/a,d/a,x.mx,x.mn};
 21 }
 22 
 23 void clear(node &x)
 24 {
 25     x.a=x.d=1;
 26     x.b=x.c=0;
 27 }
 28 
 29 void pd(int x)
 30 {
 31     merge(s[x*2],s[x]);
 32     merge(s[x*2+1],s[x]);
 33     clear(s[x]);
 34 }
 35 
 36 void build(int x,int l,int r)
 37 {
 38     clear(s[x]);
 39     if(l==r)
 40     {
 41         s[x].mn=s[x].mx=g[l];
 42         return;
 43     }
 44     int mid=(l+r)/2;
 45     build(x*2,l,mid);build(x*2+1,mid+1,r);
 46     s[x].mn=min(s[x*2].mn,s[x*2+1].mn);
 47     s[x].mx=max(s[x*2].mx,s[x*2+1].mx);
 48 }
 49 
 50 ld zhi(ld x,ld y)
 51 {
 52     return (x*y)/(x+y);
 53 }
 54 
 55 void q(int x,int l,int r)
 56 {
 57     if(l!=r)pd(x);
 58     if(qr<l||r<ql) return;
 59     if(ql<=l&&r<=qr)
 60     {
 61         if(op==1)ans=max(ans,s[x].mx);
 62         if(op==2)ans=min(ans,s[x].mn);
 63         if(op==3) s[x]=(node){1,md,0,1,s[x].mx+md,s[x].mn+md};
 64         if(op==4) s[x]=(node){md,0,1,md,zhi(s[x].mx,md),zhi(s[x].mn,md)};
 65         return;
 66     }
 67     int mid=(l+r)/2;
 68     q(x*2,l,mid);q(x*2+1,mid+1,r);
 69     if(op>=3)
 70     {
 71         s[x].mn=min(s[x*2].mn,s[x*2+1].mn);
 72         s[x].mx=max(s[x*2].mx,s[x*2+1].mx);
 73     }
 74 }
 75 
 76 int main()
 77 {
 78     scanf("%d",&n);
 79     for(int i=1;i<=n;i++)
 80         scanf("%d",&g[i]);
 81     build(1,1,n);
 82     scanf("%d",&m);
 83     while(m--)
 84     {
 85         scanf("%d%d%d",&op,&ql,&qr);
 86         if(op==1||op==2)
 87         {
 88             if(op==1) ans=-1e15;
 89             else ans=1e15;
 90             q(1,1,n);
 91             printf("%.10Lf
",ans);
 92         }
 93         else
 94         {
 95             scanf("%d",&md);
 96             q(1,1,n);
 97         }
 98     }
 99     return 0; 
100 }

C.电路图C（做不出来滑稽保命（<_<) ）

相关阅读:
ArcGIS Engine 笔记-控件类型
个人简历（公开版）
生活垃圾处理相关
如何让nextcloud支持avi文件在线播放
NextCloud前端支持播放mov文件
使用Huginn抓取Discourse论坛
使用WordPress制作微信小程序
Github 快速建库上传本地代码
BestSync多终端文件资料同步利器
ABAP-SAP HANA 数据库并发控制

原文地址：https://www.cnblogs.com/lirh04/p/12285292.html

【电路图系列】 模拟赛

【电路图系列】模拟赛