问题 F: 二师兄的纪录片（最短路或者带传送门的BFS)

问题 F: 二师兄的纪录片

二师兄护送师傅取经成功之后，成了名人，他决定重新把取经的路再走一遍，并且拍摄一部纪录片宣传路上的风光。

从东土大唐到天竺的地图，是正方形的，城市坐落在 N 行 N 列的方形地图上。地图从位置（1，1）排列到位置（N，N）。地图上每一个格子是一座城市，上下左右直接相邻的城市之间可以一天到达。

有 P 座城市住着野蛮人（野蛮城市），他们只吃红烧肉。一天三顿红烧肉，连早餐都吃红烧肉。二师兄是出家人，决定不去这些城市。

另有 Q 座城市（友好城市）希望二师兄帮他们多宣传城市风光，所以给二师兄提供一个优惠条件：如果二师兄在这座城市（X）停留三天，就可以在第四天派专机把二师兄送到另外一座城市 Y。从城市 X 飞到城市 Y 可以瞬间完成，即：二师兄在到达X城市后，可以选择四天后到达Y城市。当然，二师兄也可以选择只在X城市停留一天，然后访问X城市直接相邻的城市。

已知长安城位于地图的（1，1）位置，目的地灵山位于地图的 （N，N）位置。每一个友好城市只能直飞到另外一个城市。

请求出二师兄从长安到达灵山最少需要多少天。

输入

输入数据第一行有三个整数，分别是 N，P，Q。
整数之间用空格分开。城市坐标系X轴向下，起点为1，Y 轴向右，起点为1。
数据接下来的 P 行，每行两个整数 a,b，代表某一个野蛮城市的坐标 (a,b)。
位置信息 (a,b) 表示在 X-Y 坐标系中的位置。
再接下来的 Q 行，每行四个整数，代表友好城市 X 的坐标和从X能直飞的城市 Y 的坐标。

输出

输出数据一行，表示二师兄从长安去往灵山最少需要多少天。
如果从长安到达不了灵山，则输出-1。
二师兄在长安出发那天记为第1天，到达灵山那天的日期就是输出数据。

样例输入 Copy

【样例1】
5 7 0
1 2
2 4
3 2
3 4
4 2
4 4
5 4
【样例2】
9 27 1 
1 2 
1 6 
2 4 
2 6 
2 8 
3 2 
3 4 
3 6 
3 8 
4 2 
4 4 
4 6 
4 8 
5 4 
5 6 
5 8 
6 4 
6 6 
6 8 
7 4 
7 6 
7 8 
8 4 
8 6 
8 8 
9 4 
9 8 
6 2 8 9

样例输出 Copy

【样例1】
11
【样例2】
12

提示

样例1解释样例数据后面的解释说明当中，“.”代表可以访问的普通城市，“#”代表野蛮城市。“1”代表X城市和能从“1”直飞的城市Y。


原地图：

样例1原地图.png

到达目的地的走法：



样例2解释样例数据后面的解释说明当中，“.”代表可以访问的普通城市，“#”代表野蛮城市。“1”代表X城市和能从“1”直飞的城市Y。

原地图：

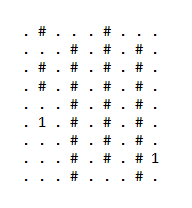
走法说明：走到 6 2 点的时候，穿越到 8 9 点。

 这个题就是一个带传送门的BFS但是我不会，我用最短路跑到

跑最短路的时候就是说，把每一个点都编上号，在每一个点向四周建图

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=2e3+100;
const int maxx=1e6+1000; 
typedef long long ll;
int a[maxn][maxn];
int s[maxn][maxn];
int n,p,q; 
int L=0;
struct node{
    int e,next;
    int w;
}edge[maxx];
int cnt=0;
int head[maxx],vis[maxx];
int dis[maxx];
void add(int u,int v,int w){
    edge[cnt].e=v;
    edge[cnt].w=w;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
void di(int s){
    for(int i=0;i<=L;i++) dis[i]=INF,vis[i]=0;
    dis[s]=0;
    while(1){
        int k=-1;
        ll minl=INF;
        for(int i=1;i<=L;i++){
            if(!vis[i]&&minl>dis[i]){
                k=i;
                minl=dis[i];
            }
        }
        if(k==-1) break;
        vis[k]=1;
        for(int i=head[k];~i;i=edge[i].next){
            int e=edge[i].e;
            if(dis[e]>dis[k]+edge[i].w){///松弛操作 也叫更新操作
                dis[e]=dis[k]+edge[i].w;
            }
        }
    }
}
int main(){
    memset(head,-1,sizeof(head));
    cin>>n>>p>>q; 
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            a[i][j]=++L;
        }
    }
    int x1,y1,x2,y2;
    for(int i=1;i<=p;i++){
        cin>>x1>>y1;
        s[x1][y1]=1;
    }
    for(int i=1;i<=q;i++){
        cin>>x1>>y1>>x2>>y2;
        add(a[x1][y1],a[x2][y2],4);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(s[i][j]==1){
                continue;
            }
            if(i-1>=1&&s[i-1][j]!=1){
                add(a[i][j],a[i-1][j],1);
                add(a[i-1][j],a[i][j],1);
            }
            if(j-1>=1&&s[i][j-1]!=1){
                add(a[i][j],a[i][j-1],1);
                add(a[i][j-1],a[i][j],1);
            }
            if(s[i+1][j]!=1){
                add(a[i][j],a[i+1][j],1);
                add(a[i+1][j],a[i][j],1);
            }
            if(s[i][j+1]!=1){
                add(a[i][j],a[i][j+1],1);
                add(a[i][j+1],a[i][j],1); 
            }
        } 
    }
    di(1);
    if(dis[a[n][n]]!=INF)
        cout<<dis[a[n][n]]+1<<endl; 
    else{
        cout<<-1<<endl;
    }
}