gcd+欧拉函数 (gcd打表）

传送门

Here GCD(i,j) means the greatest common divisor of integer i and integer j.

For those who have trouble understanding summation notation, the meaning of G is given in the following code:

输入N，求下面代码执行之后，G的值。

G=0;

for(i=1;i<N;i++)

for(j=i+1;j<=N;j++)

{

    G+=gcd(i,j);

}

/*Here gcd() is a function that finds the greatest common divisor of the two input numbers*/

Input

The input file contains at most 100 lines of inputs. Each line contains an integer N (1<N<4000001). The meaning of N is given in the problem statement. Input is terminated by a line containing a single zero.

有多组数据，以0结尾。
每行一个整数NOutput

For each line of input produce one line of output. This line contains the value of G for the corresponding N. The value of G will fit in a 64-bit signed integer.

对于每个N，输出相应的结果G。
提示:可以枚举gcd的值，再通过欧拉函数解决。Sample Input

10
100
200000
0

Sample Output

67
13015
143295493160

解析：

就是让你求出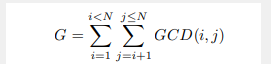

题目大意 求下面这个

假设f[n]=gcd(1,n)+gcd(2,n)+...gcd(n-1,n);

那么我们要求的ans[n]=f(2)+f(3)+f(4)+...+f(n);

所以我们只要把f[n]求出来就好了。

对gcd(x,n)进行分类，用a[i]表示gcd(x,n)=i的x的个数，意思就是从1~n-1中有多少个x0和x一样是gcd(x0,n)=i。

 这里的m表示i的种类数目，没有别的含义。

举个例子F[6]=gcd(1,6)+gcd(2,6)+gcd(3,6)+gcd(4,6)+gcd(5,6);

但是这四个我们可以给他分类

不难发现gcd(1,6)==gcd(5,6)=1; //i=1的个数为欧拉函数φ(6);

gcd(2,6)==gcd(4,6)=2gcd(1,3)=1,gcd(2,3)=1;//此处i=2的个数也就是欧拉函数φ(3)

gcd(3,6)=3gcd(1,2)=1;//此处i=3的个数也就是欧拉函数φ(2);

然后利用数目乘以最后的i

F[6]=2*1+2*2+3*1=2+4+3=9;

那么gcd(x,n)=i,可以化简成gcd(x/i,n/i)=1.与n/i互质的个数也就是欧拉函数值φ(n/i);

通过欧拉函数找到了个数，那么这个公式不就出来了吗？

    i 表示这一类的权值，φ(n/i)则表示这一类的个数

所以最终的答案

就是说：

 转自：

#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const int maxn=4e6+10000;
ll ol[maxn];
ll prime[maxn];
ll f[maxn];
ll sum[maxn]; 
int cnt=0;
void inint(){
    ol[1]=1; 
    for(int i=2;i<maxn;i++){
        if(!ol[i]) ol[i]=i-1,prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<maxn;j++){
            if(i%prime[j]==0){
                ol[i*prime[j]]=ol[i]*(prime[j]);
                break;
            }
            else{
                ol[i*prime[j]]=ol[i]*(prime[j]-1);
            }
        }
    }
}
int main(){
    inint();
    int n;
    for(int i=1;i<=maxn;i++){//f[n]代表gcd(1,n)+gcd(2,n)+...gcd(n-1,n); 
        for(int j=i+i;j<=maxn;j+=i){
            f[j]+=i*ol[j/i];
        }
    }
    sum[1]=0;
    for(int i=2;i<=maxn;i++){
        sum[i]=sum[i-1]+f[i];
    }
    while(cin>>n&&n){
        cout<<sum[n]<<endl;
    } 
} 

221. 龙哥的问题

龙哥现在有一道题，要考考大家。

给定一个整数 NN，请你求出 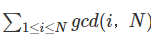的值。

输入格式

一个整数 N。

输出格式

一个整数表示结果。

数据范围

1<N<2e31

输入样例：

6

输出样例：

15


这个题就是上一个的变种，但是这个题的数据范围很大n<=1e9.
还是哪样把gcd(x,n)==i中的个数找出来,就是gcd(x/i,n/i)==1的个数
就是i*ol[n/i]，
然后就是枚举这个i，这个i肯定是n的因子

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=5e6+100;
int biaoji[maxn];
int prime[maxn];
int ol[maxn];
int cnt=0;
int oul(ll x){
    ll ans=x;
    for(ll i=2;i*i<=x;i++){
        if(x%i==0){
            ans=ans/i*(i-1);
            while(x%i==0){
                x/=i;
            }
        }
    }
    if(x>1){
        ans=ans/x*(x-1);
    }
    return ans;
}
int main(){
    ll n;
    cin>>n;
    ll ans=0;
    for(ll i=1;i*i<=n;i++){
        if(n%i==0){
            ans+=i*oul(n/i);
            if(i*i!=n){
                ans+=(n/i*oul(i));
            }
        }
    }
    cout<<ans<<endl;   

}