图算法系列-图的简单实现

最近看了很多介绍图算法的文章，发现网上可以搜到的资料比较少，所以打算在这写一个介绍图算法的系列文章，一方面是帮助自己整理，另一方面也给大家分享下这方面的知识。

1.1图的定义：
图（graph）由顶点（vertex）和边（edge）的集合组成，每一条边就是一个点对（v,w)。

图的种类：地图，电路图，调度图，事物，网络，程序结构

图的属性：有V个顶点的图最多有V*（V-1）/2条边

1.2图的ADT：

struct Edge{
int v,w;
Edge(int a=-1,int b=-1):v(a),w(b){}
};

class Graph
{
private:
//
public:
Graph(int,bool);
~Graph();
int V() const;//顶点
int E() const;//边
bool directed() const;//是否有方向
int insert(Edge);
int remove(Edge);
bool edge(int,int);
//迭代器
class adjIterator
{
public:
adjIterator(const Graph&,int);
int begin();
int next();
bool end();
};
};

图的构造函数将图中可能的最大顶点数作为一个参数。

1.3邻接矩阵：
邻接矩阵是一个元素为bool值的V*V矩阵，若图中存在一条连接顶点V和W的边，折矩阵adj[v][w]=1,否则为0。占用的空间为V*V，当图是稠密时，邻接矩阵是比较合适的表达方法。

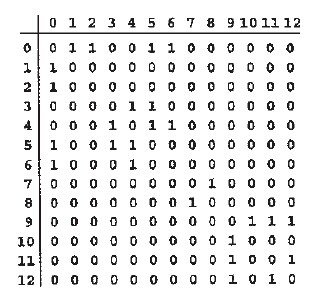
//graph ADT实现（邻接矩阵）

class DenseGraph
{
public:
DenseGraph(int v,bool digraph=false):adj(v),Vcnt(v),Ecnt(0),diGraph(digraph){
for(int i=0;i<v;++i)
adj[i].assign(v,false);//将邻接矩阵初始化为false
}
int V() const{
return Vcnt;
}
int E() const{
return Ecnt;
}
bool directed() const{
return diGraph;
}
void insert(Edge e)
{
int v=e.v,w=e.w;
if(adj[v][w]==false) Ecnt++;
adj[v][w]=true;
if(!digraph) adj[w][v]=true;
}
void remove(Edge e)
{

int v=e.v,w=e.w;
if(adj[v][w]==true) Ecnt--;
adj[v][w]=false;
if(!digraph) adj[w][v]=false;
}
bool edge(int v,int w) const
{
return adj[v][w];
}
class adjIterator;
friend class adjIterator;

private:
int Vcnt;//顶点数
int Ecnt;//边数
bool diGraph;//是否有向图
vector< vector<bool> > adj;//邻接矩阵
};

//邻接矩阵的迭代器，返回顶点vertex的下一个相邻的顶点
class DenseGraph::adjIterator
{
public:
adjIterator(const DenseGraph &g,int vertex):
G(g),v(vertex),i(-1){}
int begin()
{
i=-1;
return next();
}
int next()
{
for(i++;i<G.V();++i)
if(G.adj[v][i]==true) return i;
return -1;
}
bool end()
{
return i>=G.V();
}
private:
const DenseGraph &G;
int i,v;
}；

1.4邻接表的表示
对于非稠密的图，使用邻接矩阵有点浪费存储空间，可以使用邻接表，我们维护一个链表向量，给定一个顶点时，可以立即访问其链表,占用的空间为O(V+E)。

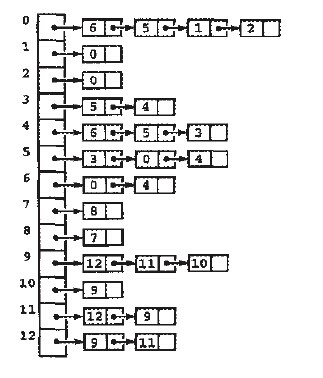
//程序：Graph的邻接表实现

class SparseGraph()
{
public:
SparseGraph(int v,bool digraph=false):
Vcnt(v),Ecnt(0),diGraph(digraph){
adj.assign(v,0);
}
SparseGraph(const SparseGraph& G);
~SparseGraph();
int V() const{
return Vcnt;
}
int E() const{
return Ecnt;
}
bool directed(){
return digraph;
}
//往图中插入一条边
void insert(Edge e){
int v=e.v,w=e.w;
adj[v]=new node(w,adj[v]);
if(!diGraph) adj[w]=new node(v,adj[w]);
Ecnt++;
}
void remove(Edge e);
bool Edge(int v,int w) const;
class adjIterator;//邻接表的迭代器
friend class adjIterator;//把迭代器类设置为友元类
private:
int Vcnt,Ecnt;
bool diGraph;
struct node
{
int v;
node* next;
node(int x,node* t):v(x),next(t){}
};
typedef node* link;
vector<link> adj;//邻接表
}；

//邻接表迭代器的实现
class SparseGraph::adjIterator
{
public:
adjIterator(const SparseGraph& g,int v):
G(g),v(v),curLink(0){}
adjIterator(const adjIterator&);
~adjIterator();
int begin(){
curLink=adj[v];
return curLink?curLink-v:-1;

}
int next(){
if(curLink) curLink=curLink->next;
return curLink?curLink->v:-1;
}
bool end(){
return curLink==0;
}
private:
const SparseGraph& G;
int v;//顶点编号
link curLink;
};

1.5简单路径搜索
给定两个顶点，图中是否存在一条连接起来的简单路径呢？
比如给定顶点V和W，对于和V相邻的每个顶点t,是否存在从t到W的简单路径，然后递归调用，我们使用一个顶点访问向量visited来对顶点标记防止重复访问。

//程序：简单路径搜索

template <class Graph> class SearchPath
{

public:
SearchPath(const Graph& g,int v,int w):
G(g),visited(g.V(),false){
found=search(v,w);
}
bool existed() const
{
return found;
}
private:
const Graph& G;
vector<bool> visited;
bool found;
bool search(int v,int w)
{
if(v=w) return true;
visited[v]=true;

typename Graph::adjIterator ite(G,v);
for(int t=ite.begin();!ite.end();t=ite.next())
if(!visited[t])
if(search(t,w)) return true;
return false;
}
};

 参考资料：维基百科http://en.wikipedia.org/wiki/Category:Graph_algorithms

　　　　　　Graph algorithm:http://www-users.cs.umn.edu/~karypis/parbook/Lectures/AG/chap10_slides.pdf

　　　　　　原文地址：http://lippiouyangonline.info/algorithm/2013/12/29/graph.html