众所周知,“八皇后” 问题是求解在国际象棋棋盘上摆放 8 个皇后,使得两两之间互不攻击的方案数。
已经学习了很多算法的小蓝觉得 “八皇后” 问题太简单了,意犹未尽。作为一个国际象棋迷,他想研究在 N×M 的棋盘上,摆放 K 个马,使得两两之间互不攻击有多少种摆放方案。
由于方案数可能很大,只需计算答案除以 1000000007 (即 109+7) 的余数。
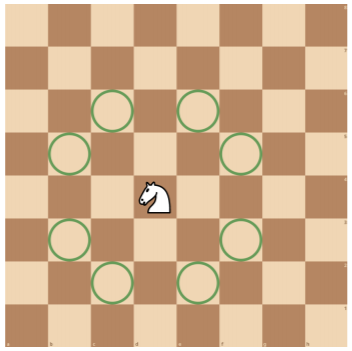
如下图所示,国际象棋中的马摆放在棋盘的方格内,走 “日” 字,位于 (x,y) 格的马(第 x 行第 y 列)可以攻击 (x+1,y+2)、(x+1,y−2)、(x−1,y+2)、(x−1,y−2)、(x+2,y+1)、(x+2,y−1)、(x−2,y+1) 和 (x−2,y−1) 共 8 个格子。
输入格式
输入一行包含三个正整数 N,M,K,分别表示棋盘的行数、列数和马的个数。
输出格式
输出一个整数,表示摆放的方案数除以 1000000007 (即 109+7) 的余数。
数据范围
对于 5% 的评测用例,K=1;
对于另外 10% 的评测用例,K=2;
对于另外 10% 的评测用例,N=1;
对于另外 20% 的评测用例,N,M≤6,K≤5;
对于另外 25% 的评测用例,N≤3,M≤20,K≤12;
对于所有评测用例,1≤N≤6,1≤M≤100,1≤K≤20。
输入样例1:
1 2 1
输出样例1:
2
输入样例2:
4 4 3
输出样例2:
276
输入样例3:
3 20 12
输出样例3:
914051446
暴搜会T。看到范围很小故考虑状压。因为m最大会到100,而n最大才为6,因此不能对行状压只能对列状压。注意到一个马可能发生冲突的位置是与其距离不超过2的位置,因此设(dp[i][j][k][w])代表前i行且第i - 1行状态为j,第i行状态为k,用了w个马的方案数。转移方程见代码。注意转移时以及枚举j, k的时候要判断是否冲突,以及注意初始化和遍历的顺序(i为阶段要放在最外面)。
#include <bits/stdc++.h>
#define MOD 1000000007
using namespace std;
int n, m, K;
long long dp[120][1 << 6][1 << 6][25];//dp[i][j][k][w]表示前i列且当前列的前列状态为j,当前列状态为k,用掉w个马的方案数
int get(int x) {
int xx = x, ans = 0;
while(xx > 0) {
if(xx & 1) {
ans++;
}
xx /= 2;
}
return ans;
}
int main() {
cin >> n >> m >> K;
dp[0][0][0][0] = 1;//注意初始化
for(int i = 1; i <= m; i++) {
for(int p1 = 0; p1 < (1 << n); p1++) {
for(int p2 = 0; p2 < (1 << n); p2++) {
if(((p1 >> 2) & p2) || (p1 & (p2 >> 2))) {//转移之前的
continue;
} else {
for(int p3 = 0; p3 < (1 << n); p3++) {
if(((p3 >> 2) & p2) || (p3 & (p2 >> 2))) {//当前列这么放会和之前的发生冲突
continue;
}
if(((p3 >> 1) & p1) || (p3 & (p1 >> 1))) {
continue;
}
int num = get(p3);//当前第i行的马的个数
for(int k = num; k <= K; k++) {
dp[i][p2][p3][k] = (dp[i][p2][p3][k] + dp[i - 1][p1][p2][k - num]) % MOD;
}
}
}
}
}
}
long long ans = 0;
for(int i = 0; i < (1 << n); i++) {
for(int j = 0; j < (1 << n); j++) {
ans = (ans + dp[m][i][j][K]) % MOD;
}
}
cout << ans;
return 0;
}