题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3个整数,表示一个操作,具体如下:
操作1: 格式:1 x k 含义:将第x个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
样例说明:
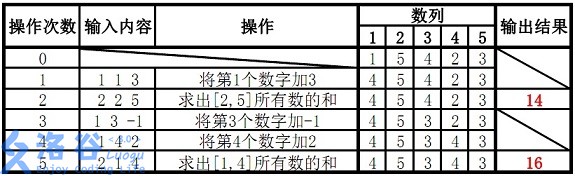
故输出结果14、16
一道简单的模板题,没有什么特别解题思路。
AC代码:
#include<iostream> using namespace std; int tree[500004]; int n,m; int lowbit(int k) { return k & (-k); } void mk(int s,int d){ while(s <= n){ tree[s] += d; s += lowbit(s); } } int jia(int k){ int ans = 0; while(k != 0){ ans += tree[k]; k -= lowbit(k); } return ans; } int main(){ cin >> n >> m; for(int i = 1;i <= n; i++) { int a; cin>>a; mk(i,a); } for(int i = 1;i <= m; i++) { int u,x,y; cin >> u; if(u == 1) { cin >> x >> y; mk(x,y); } if(u == 2){ cin >> x >> y; cout << jia(y) - jia(x-1) << endl; } } return 0; }