[算法]后缀数组

前言
这篇博客真难写，暂定待更

定义
后缀数组[SuffixArray]是一个一维数组，简称SA，它保存1到n的某个排列(SA[1] ,SA[2],dots,SA[n])，并且保证(Suffix(SA[i])<Suffix(SA[i+1]))，(1 leq i < n) 。也就是将s的n个后缀按字典序从小到大进行排序之后把排好序的后缀的编号顺次放入SA中。

我们先从后缀数组的入门题洛咕P3809讲起
名词解释
后缀[suffix]:
类似前缀，在字符串处理中意为对于一个初始字符串，以该字符串中任意元素为起始元素，最后一个元素为末尾元素的字串，即为该字符串的后缀
基数排序[Radix Sort]:
基数排序是桶排序的扩展，复杂度(Theta(n m log(r)))，其中r为所采取的基数，而m为堆数
基数排序[radix sort]属于"分配式排序[distribution sort]"，又称“桶子法”[bucket sort]或[bin sort]，它透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用
以上内容节选自百度百科
好了接下来讲如何构造后缀数组
构造后缀数组
首先我们将后缀编号

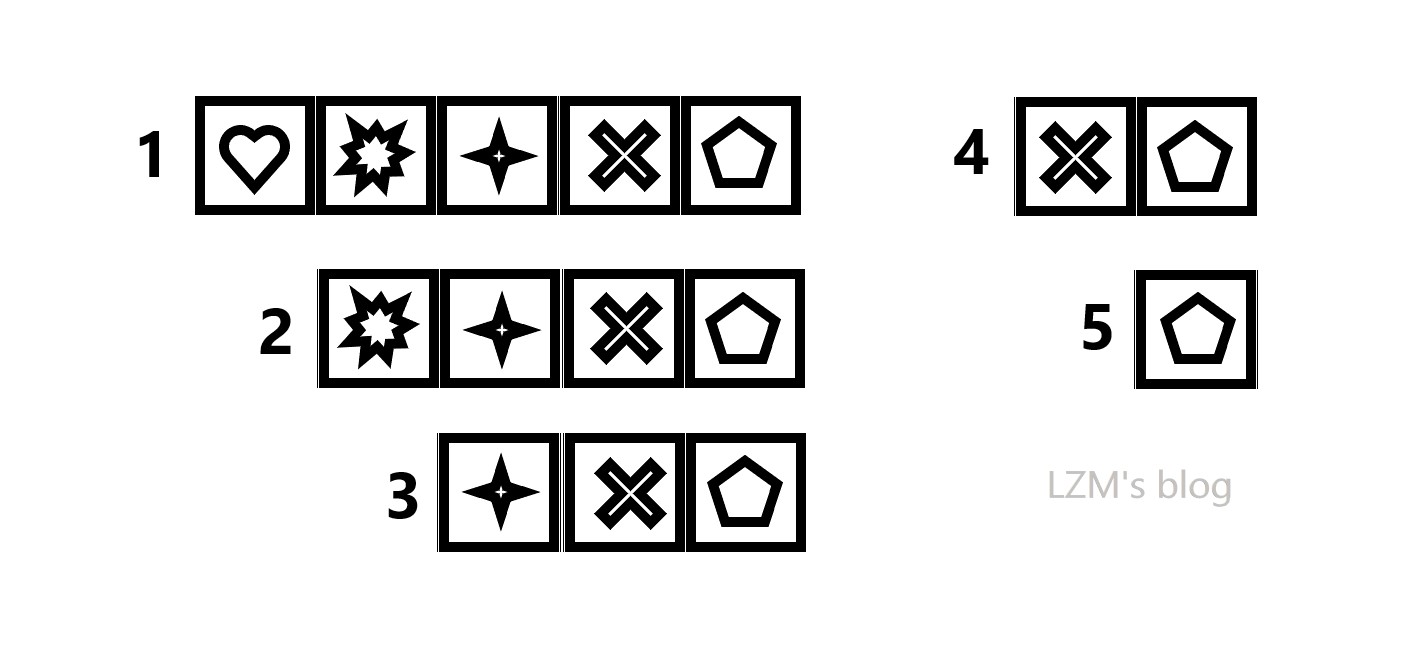
上图中编号为1的字符串为初始串，那么按如图所示给它编号为1-n。
s[i]:字符串的第i位
sa[i]:就是后缀数组，排名为i的后缀的编号
fst[i]:从编号为i的后缀的排名，即记录第一关键字排名(备注：在很多博客里这个数组的名字叫rank)
sec[i]:基数排序的第二关键字，表示以第二关键字排序时排名为i的后缀的编号
buk:桶
程序原理：
首先我们得形象理解fst,sec这两个十足。简单来说若当前后缀长度为len，fst是针对前(frac{len}{2})个字符的，sec是针对后(frac{len}{2})个字符的。
构造初始状态，按第一个字符基数排序的到了一个序列，此时第一个字母的相对关系我们已经知道了，暴力做法按第二个字母继续排序，但事实上我们需要这样做吗？
实际上有一点非常重要：编号为i的后缀的第二个字母，实际是编号为i+1的后缀的第一个字母。还有这种操作？就是有这种操作。又发现编号为i的后缀的第3,4个字母恰好是编号为i+2的后缀的前两个字母。天哪。
这个性质有什么意义呢？
这就意味如果我们不断继续下去，我们珂以使用上一层的sec更新本层的fst，而不需额外计算
于是之后我们将会用到(i+4,i+8,i+16,dots)的后缀计算i的第一关键字，我们珂以将其简单理解为一种倍增
于是我们愉快的一直计算，知道所有后缀的排名不同，然后结束
由于最多倍增计算到n，所以复杂度最大为(Theta(n log_2(n)))
这样讲珂能(确实)很难理解，我们直接进入程序流程。

程序流程：
初始化：
根据字符串构造桶，并顺便初始化fst数组为该字母的ASCII码
这里我们要给桶求一个前缀，求玩前缀有什么好处呢？这珂以使桶中的数直接对应排名，方便计算
倍增循环部分：
待更。

P3809代码实现：

#include <cstdio>
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>

using namespace std;

namespace SuffixArray{ 
    //uses cstring, algorithm, cstdio. Program by lukelin
    #define MAXN 1000010 //len of max length
    #define MAXC 122 //len of max char (0, 255]
    #define ri register int
    int sa[MAXN], rnk[MAXN], fst[MAXN], sec[MAXN], buk[MAXN];
    char s[MAXN]; int s_len; int rnk_cnt;
    inline void clearBuk(){for (ri i = 0; i <= rnk_cnt; ++i) buk[i] = 0;}
    inline void getPrefixBuk(){for (ri i = 1; i <= rnk_cnt; ++i) buk[i] += buk[i - 1];}
    inline void printSA(){for (int i = 1; i <= s_len; ++i) printf("%d%c", sa[i], ((i == s_len)) ? '
' : ' ');}
    void getSuffixArray(){
        s_len = strlen(s); rnk_cnt = MAXC;
        clearBuk();
        for (int i = 1; i <= s_len; ++i) ++buk[fst[i] = s[i - 1]];
        getPrefixBuk();
        for (int i = s_len; i > 0; --i) sa[buk[fst[i]]--] = i;
        for (int k = 1; k <= s_len; k <<= 1){
            int cnt = 0;
            for (int i = s_len - k + 1; i <= s_len; ++i) sec[++cnt] = i;
            for (int i = 1; i <= s_len; ++i) if (sa[i] > k) sec[++cnt] = sa[i] - k;
            clearBuk();
            for (int i = 1; i <= s_len; ++i) ++buk[fst[i]];
            getPrefixBuk();
            for (int i = s_len; i >= 1; --i) sa[buk[fst[sec[i]]]--] = sec[i], sec[i] = 0;
            std::swap(fst, sec);
            fst[sa[1]] = 1, rnk_cnt = 1;
            for (int i = 2; i <= s_len; ++i)
                fst[sa[i]] = (sec[sa[i]] == sec[sa[i - 1]] && sec[sa[i] + k] == sec[sa[i - 1] + k]) ? rnk_cnt : (++rnk_cnt);
            if (rnk_cnt == s_len) break;
        }
    }
    #undef MAXN
    #undef MAXC
    #undef ri
};

int main(){
    cin >> SuffixArray::s;
    SuffixArray::getSuffixArray();
    SuffixArray::printSA();
    return 0;
}

后缀数组思想
(未完待更)