以前在工作中遇到了一个数据错误的问题,顺便写下 用 Math.Net 解决的思路。
1. 错误的数据#
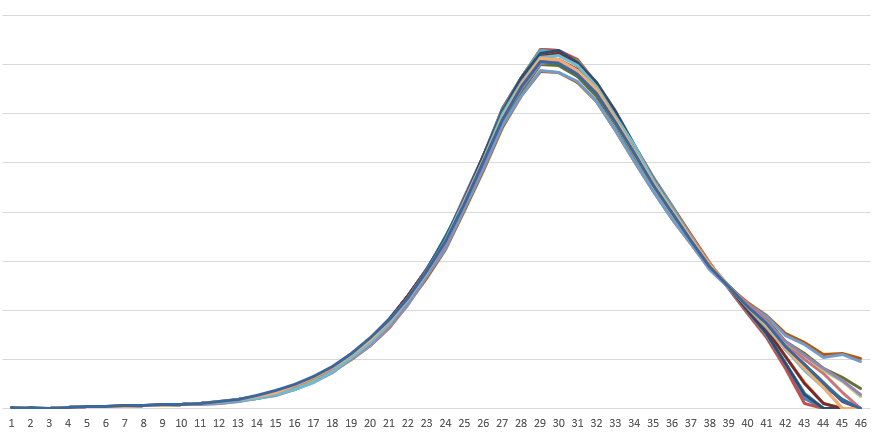
上图是同一组探测器在同一天采集到的 19 次数据,总体来说重复性不错,但很明显最后 8 个探测器出了问题,导致采集到的数据在最后八个点一片混乱。即使把其中看起来最好的一组数据拿出来使用多项式拟合,也可以看出最后几个点没有落在拟合曲线上(只拟合最后 14 个点):
虽然我知道这是硬件问题,但是遇到事情不能坐以待毙,软件方面也许可以做些什么。既然我从上图中得知出了最后几个点之外,其它数据都在拟合曲线上,那我可以使用前面几个点的拟合结果预测后面几个点并替换掉出错的数据,从而得到一组看起来正常的数据。
2. 曲线拟合与数据预测#
曲线拟合(curve fitting)是指选择适当的曲线类型来拟合观测数据,以便观察两组数据之间的内在联系,了解数据之间的变化趋势。
在数据分析时,我们有时需要通过已有数据来预测未来数据。在一些复杂的数据模型中,数据维度很多,数据之间的关系很复杂,我们可能会用到深度学习的算法。但是在一些简单的数据模型中,数据之间有很明显的相关性,那我们就可以使用简单的曲线拟合来预测未来的数据。
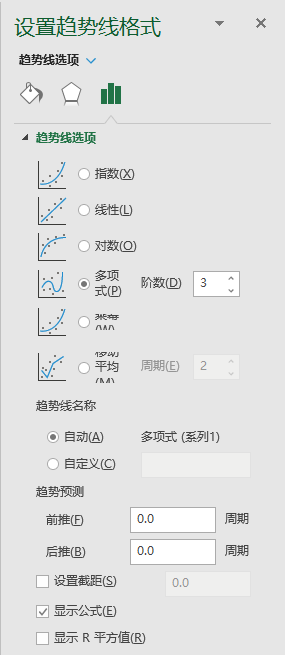
这些工作都可以使用 Excel 完成,先来尝试一下。把某组数据最后14个点(只选取峰值右边的14个点是因为容易计算)放进Excel中,插入一个散点图,右键点击其中的蓝色散点,选择添加趋势线:
然后在右侧出现的设置趋势线格式中选择多项式,阶数为 3,勾选显示公式:
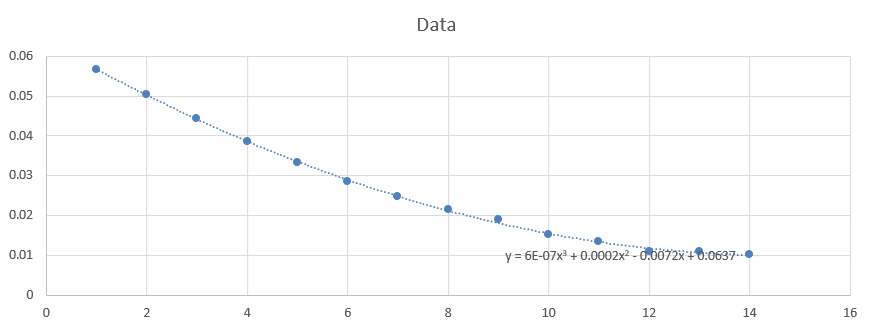
可以看到,曲线图中出现了一条虚线的曲线,并显示了对应的公式为 y = 6E-07x3 + 0.0002x2 - 0.0072x + 0.0637:
如果需要预测数据,可以修改前推数字以得到后面几个周期的数据。
3. 使用 Math.Net 进行曲线拟合#
当然我不可能对每一条数据都扔进 Excel 里进行拟合。在 C# 中我们可以使用 Math.Net 进行非线性拟合。
Math.Net 是一个开源项目,旨在构建和维护涵盖基础数学的工具箱,以满足 .Net 开发人员的高级需求和日常需求。其中 Math.NET Numerics 旨在为科学、工程和日常使用中的数值计算提供方法和算法。涵盖的主题包括特殊函数,线性代数,概率模型,随机数,插值,积分变换等等。
要使用 Math.NET Numerics,首先安装它的 Nuget 包:
Install-Package MathNet.Numerics
Math.NET Numerics 提供了 Fit.Polynomial 函数用作多项式拟合,如以下代码所示,其中 X 是 X 轴的数组, Y 是 Y 轴的数组, 函数的第三个参数是多项式的阶数,这里用 2 作为阶数。
double[] X = Enumerable.Range(1, 6).Select(r => (double)r).ToArray();
double[] Y = values.ToArray();
double[] parameters = Fit.Polynomial(X, Y, 2);
返回的结果是最佳拟合参数的数组 [p0,p1,p2,…,pk],将其带入公式 p0 + p1×x + p2×x2 + ... + pk×xk 即可算出对应的拟合数据。完整的代码如下,在这个示例里,我只需要用倒数第9到14个数据,通过 Fit.Polynomial 获得一个多项式的方程 ( f(x) = p0 + p1×x + p2×x2 ),然后用这个方程计算出后面 8 个点的数据替换原本出错的数据:
double[] X = Enumerable.Range(1, 6).Select(r => (double)r).ToArray();
double[] Y = values.ToArray();
double[] parameters = Fit.Polynomial(X, Y, 2);
List<double> result = new List<double>();
for (int i = 1; i < 15; i++)
{
result.Add(parameters[0] + parameters[1] * i + parameters[2] * i * i );
}
for (int i = 0; i < 8; i++)
{
data[data.Count - 1 - i] = result[result.Count - 1 - i];
}
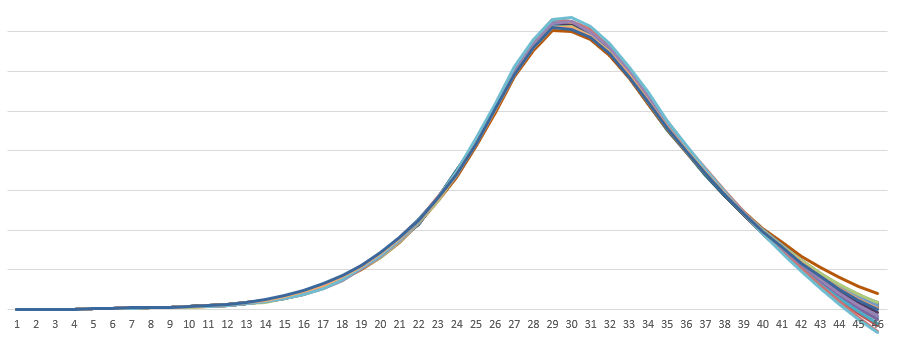
替换后的结果如上所示,整体符合前面数据的趋势,使用这组数据进行运算也能得到很好的结果。
4. 最后#
Math.Net 是一个强大的项目,这篇文章只介绍了它所有功能的冰山一角。想了解更多可以参考官方文档,或参考博客园上的文章,例如:
【目录】开源Math.NET基础数学类库使用总目录 - 数据之巅 - 博客园
5. 参考#
Curve Fitting Linear Regression
【目录】开源Math.NET基础数学类库使用总目录 - 数据之巅 - 博客园
6. 源码#
作者:Dino.C
出处:https://www.cnblogs.com/dino623/p/curve_fitting_and_data_prediction_using_math_net.html
版权:本文采用「CC BY 4.0」知识共享许可协议进行许可。