一、什么是二叉树?
1.1 定义
二叉树,是度为二的树,二叉树的每一个节点最多只有二个子节点,且两个子节点有序。
1.2 二叉树的重要特性
(1)二叉树的第 i 层上节点数最多为 2n-1;
(2)高度为 k 的二叉树中,最多有 2k-1个节点;
(3)在任意一棵二叉树中,如果终端节点的度为 n,度为 2 的节点数为 m,则 n=m+1;
(4)二叉树的子树有左右之分,顺序不能颠倒。
1.3 特殊二叉树
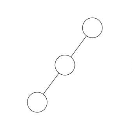
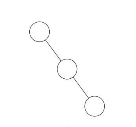
斜树:所有的结点都只有左子树的二叉树叫左斜树,有结点都是只有右子树的二叉树叫右斜树。
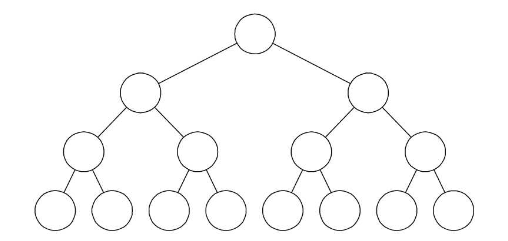
满二叉树:如果所有分支结点都存在左子树和右子树,并且所有的叶子都在同一层上,就称为满二叉树。
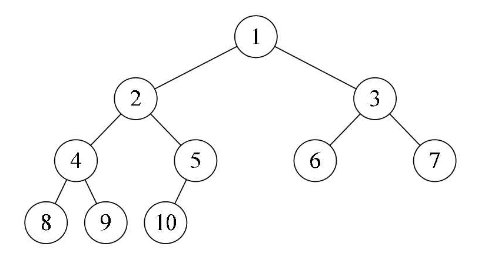
完全二叉树:如果二叉树的深度为 k,则除第 k 层外其余所有层节点的度都为 2,且叶子节点从左到右依次存在,将满二叉树的最后一层从左到右依次删除若干节点就得到满二叉树。满二叉树是一棵特殊的完全二叉树,但完全二叉树不一定是满二叉树。
因为二叉树的顺序存储结构缺点很明显,不能反应逻辑关系;对于特殊的二叉树(左斜树、右斜树),浪费存储空间。所以二叉树顺序存储结构一般只用于完全二叉树,因此这里只重点介绍二叉树的链式存储结构。
二、什么是链式二叉树?
链式二叉树:采用链式存储结构的二叉树。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法。
以下是链式二叉树的结点结构定义:
/* 二叉树结点结构 */
typedef struct BiTNode
{
ElemType data; // 结点数据
struct BiTNode *lchild, *rchild; // 左右孩子指针
}BiTNode, BiTree;
结构示意图如下图所示:
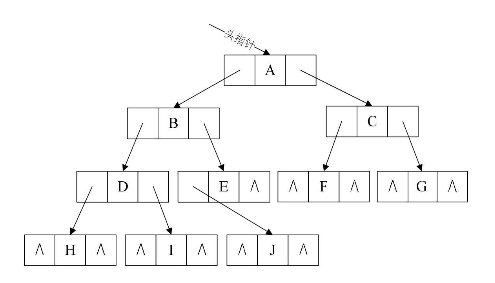
三、具体实现
3.1 二叉树的遍历
| 二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。 |
二叉树的遍历次序不同于线性结构,最多也就是从头至尾、循环、双向等简单的遍历方式。树的结点之间不存在唯一的前驱和后继关系,在访问一个结点后,下一个被访问的结点面临着不同的选择。
二叉树的遍历方式可以很多,如果我们限制了从左到右的习惯方式,那么主要就分为四种:
1. 前序遍历
规则是若二叉树为空,则返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。如下图所示,遍历顺序为:根节点-->左孩子-->右孩子,结果为:ABDGHCEIF。
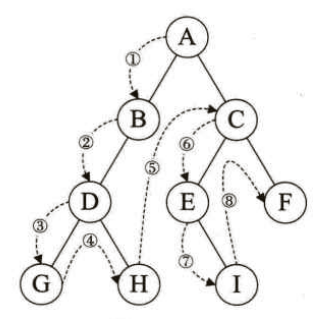
二叉树的定义是用递归的方式,所以,实现遍历算法也可以采用递归,而且极其简洁明了。实现代码如下:
// 前序遍历(递归方式)
void preOrderTraverse(BiTree *T)
{
// 判断二叉树是否存在
if (T == NULL)
return;
printf("%c", T->data); // 显示结点数据,可以更改为其它对结点操作
preOrderTraverse(T->lchild); // 再前序遍历左子树
preOrderTraverse(T->rchild); // 最后前序遍历右子树
}
对于结点 B,只会执行左子树遍历函数;到了结点 D,先执行左子树遍历函数,再执行右子树遍历函数;至此结点 A 的左子树递归完毕,然后就会回到结点 A,开始执行结点 A 的右子树遍历函数。
2. 中序遍历
规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。如下图所示,遍历顺序为:左孩子-->根节点-->右孩子,结果为:GDHBAEICF。
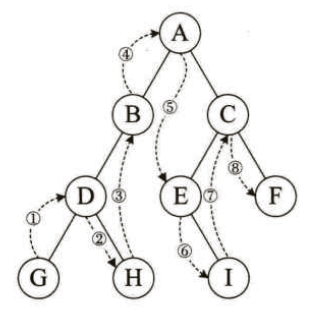
那么二叉树的中序遍历算法是如何呢?哈哈,别以为很复杂,它和前序遍历算法仅仅只是代码的顺序上的差异。实现代码如下:
// 中序遍历(递归方式)
void inOrderTraverse(BiTree *T)
{
// 判断二叉树是否存在
if (T == NULL)
return;
inOrderTraverse(T->lchild); // 中序遍历左子树
printf("%c", T->data); // 显示结点数据,可以更改为其它对结点操作
inOrderTraverse(T->rchild); // 最后中序遍历右子树
}
第一轮遍历到结点 D,接着执行左子树遍历函数,T指向结点 G,才到第一次执行 printf 的时候;然后回到结点 D,显示其数据,执行右子树遍历函数,显示结点 H 的数据。
3. 后序遍历
规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点。如下图所示,遍历顺序为:左孩子-->右孩子-->根节点,结果为:GHDBIEFCA。
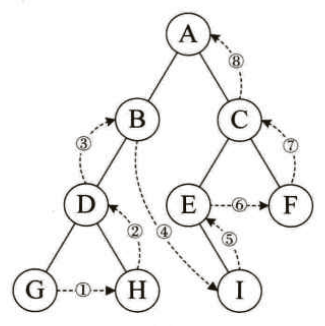
实现代码如下:
// 后序遍历(递归方式)
void postOrderTraverse(BiTree *T)
{
// 判断二叉树是否存在
if (T == NULL)
return;
postOrderTraverse(T->lchild); // 先后序遍历左子树
postOrderTraverse(T->rchild); // 再后序遍历右子树
printf("%c", T->data); // 显示结点数据,可以更改为其它对结点操作
}
4. 层序遍历
规则是若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。如下图所示,结果为:ABCDEFGHI。
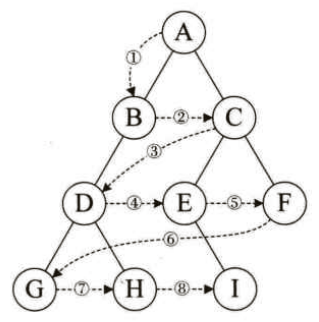
有同学会说,研究这么多遍历的方法干什么呢?
我们用图形的方式来表现树的结构,应该说是非常直观和容易理解,但是对于计算机来说,它只有循环、判断等方式来处理,也就是说,它只会处理线性序列,而我们刚才提到的四种遍历方法,其实都是在把树中的结点变成某种意义的线性序列,这就给程序的实现带来了好处。另外不同的遍历提供了对结点依次处理的不同方式,可以在遍历过程中对结点进行各种处理。
3.2 二叉树的建立
如果我们要在内存中建立一个如下图左这样的树,为了能让每个结点确认是否有左右孩子,我们对它进行了扩展,变成下图右的样子,也就是将二叉树中每个结点的空指针引出一个虚结点,其值为一特定值,比如 “#”。我们称这种处理后的二叉树为原二叉树的扩展二叉树。扩展二叉树就可以做到一个遍历序列确定一棵二叉树了。比如下图的前序遍历序列就为 AB#D##C##。
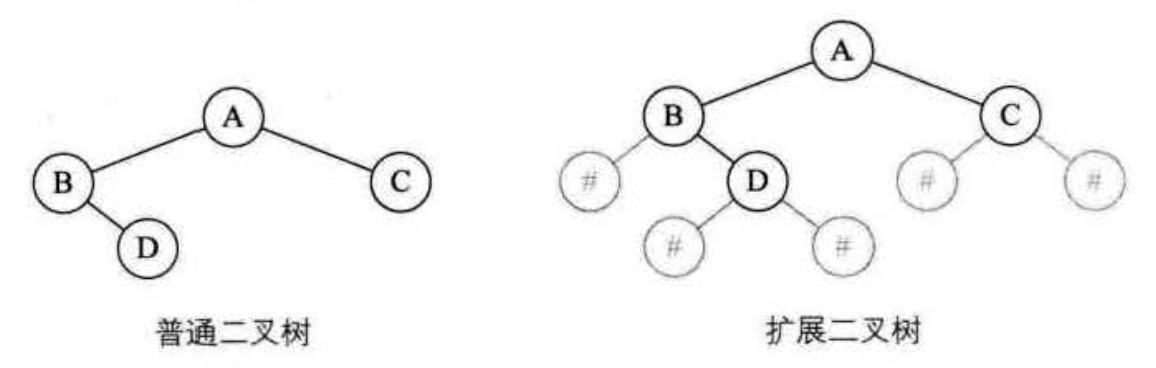
有了这样的准备,我们就可以来看看如何生成一棵二叉树了。假设二叉树的结点均为一个字符,我们把先前的前序遍历序列 ABDG##H###CE#I##F## 赋给一个字符数组。实现代码如下:
// 建立二叉树 [按前序输入二叉树中结点的值(一个字符)]
void createBiTree(BiTree **T)
{
ElemType ch;
// str是全局数组,指向 'length' + "ABDG##H###CE#I##F##" 字符串
ch = str[index++];
if (ch != '#')
{
*T = (BiTree *)malloc(sizeof(BiTNode));
if (!*T)
return;
(*T)->data = ch; // 生成根结点
createBiTree(&(*T)->lchild); // 构造左子树
createBiTree(&(*T)->rchild); // 构造右子树
}
else
{
*T = NULL; // 值为#表示空树
}
}
其实建立二叉树,也是利用了递归的原理。只不过在原来应该是打印结点的地 方,改成了生成结点、给结点赋值的操作而已。所以大家理解了前面的遍历的话,对于这段代码就不难理解了。
当然,你完全也可以用中序或后序遍历的方式实现二叉树的建立,只不过代码里生成结点和构造左右子树的代码顺序交换一下。另外,输入的字符也要做相应的更改。比如上图的扩展二叉树的中序遍历字符串就应该为 #B#D#A#C#,而后序字符串应该为 ###DB##CA。
四、完整程序
#include "stdio.h"
#include "stdlib.h"
#include "string.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如TRUE等 */
typedef char ElemType;
/* 二叉树结点结构 */
typedef struct BiTNode
{
ElemType data; // 结点数据
struct BiTNode *lchild, *rchild; // 左右孩子指针
}BiTNode, BiTree;
//Status strAssign(ElemType T[24], ElemType *chars); // 构建字符串
Status initBiTree(BiTree **T); // 初始化二叉树
void createBiTree(BiTree **T); // 建立二叉树 [按前序输入二叉树中结点的值(一个字符)]
void preOrderTraverse(BiTree *T); // 前序遍历(递归方式)
void inOrderTraverse(BiTree *T); // 中序遍历(递归方式)
void postOrderTraverse(BiTree *T); // 后序遍历(递归方式)
void destroyBiTree(BiTree **T); // 销毁二叉树
Status isEmpty(BiTree *T); // 判断是否是空二叉树
int getBiTreeDepth(BiTree *T); // 获得二叉树的深度
ElemType getRoot(BiTree *T); // 获得二叉树的根
ElemType getNodeValue(BiTree *p); // 获得指定结点的值
void setValue(BiTree *p, ElemType value); // 给指定节点设置值
/* 用于构造二叉树********************************** */
int index = 1; // 因为str的头字节是字符串的长度,所以从1开始插入
ElemType str[24] = {19, 'A','B','D','G','#','#','H','#','#','#','C','E','#','I','#','#','F','#','#'};
// 初始化二叉树
Status initBiTree(BiTree **T)
{
*T = NULL;
return TRUE;
}
// 建立二叉树 [按前序输入二叉树中结点的值(一个字符)]
void createBiTree(BiTree **T)
{
ElemType ch;
// str是全局数组,指向 'length' + "ABDG##H###CE#I##F##" 字符串
ch = str[index++];
if (ch != '#')
{
*T = (BiTree *)malloc(sizeof(BiTNode));
if (!*T)
return;
(*T)->data = ch; // 生成根结点
createBiTree(&(*T)->lchild); // 构造左子树
createBiTree(&(*T)->rchild); // 构造右子树
}
else
{
*T = NULL; // 值为#表示空树
}
}
// 前序遍历(递归方式)
void preOrderTraverse(BiTree *T)
{
// 判断二叉树是否存在
if (T == NULL)
return;
printf("%c", T->data); // 显示结点数据,可以更改为其它对结点操作
preOrderTraverse(T->lchild); // 再前序遍历左子树
preOrderTraverse(T->rchild); // 最后前序遍历右子树
}
// 中序遍历(递归方式)
void inOrderTraverse(BiTree *T)
{
// 判断二叉树是否存在
if (T == NULL)
return;
inOrderTraverse(T->lchild); // 中序遍历左子树
printf("%c", T->data); // 显示结点数据,可以更改为其它对结点操作
inOrderTraverse(T->rchild); // 最后中序遍历右子树
}
// 后序遍历(递归方式)
void postOrderTraverse(BiTree *T)
{
// 判断二叉树是否存在
if (T == NULL)
return;
postOrderTraverse(T->lchild); // 先后序遍历左子树
postOrderTraverse(T->rchild); // 再后序遍历右子树
printf("%c", T->data); // 显示结点数据,可以更改为其它对结点操作
}
// 销毁二叉树
void destroyBiTree(BiTree **T)
{
if (*T != NULL)
{
if ((*T)->lchild) // 有左孩子
destroyBiTree(&(*T)->lchild); // 销毁左孩子子树
if ((*T)->rchild) // 有右孩子
destroyBiTree(&(*T)->rchild); // 销毁右孩子子树
free(*T); // 释放根结点
*T = NULL; // 空指针赋NULL
}
}
// 判断是否是空二叉树
Status isEmpty(BiTree *T)
{
return T == NULL ? TRUE : FALSE;
}
// 获得二叉树的深度
int getBiTreeDepth(BiTree *T)
{
if (!T)
return 0;
int left = getBiTreeDepth(T->lchild); // 获得左子树的深度
int right = getBiTreeDepth(T->rchild); // 获得右子树的深度
return left>right ? left + 1 : right + 1;
}
// 获得二叉树的根
ElemType getRoot(BiTree *T)
{
if (isEmpty(T))
return ' ';
else
return T->data;
}
// 获得指定结点的值
ElemType getNodeValue(BiTree *p)
{
return p->data;
}
// 给指定节点设置值
void setValue(BiTree *p, ElemType value)
{
p->data = value;
}
int main()
{
BiTree *T;
// 初始化二叉树
initBiTree(&T);
// 建立二叉树
createBiTree(&T);
// 判断是否是空二叉树 | 获得二叉树的深度
printf("构造空二叉树后,树空否?%d(1:是 0:否) 二叉树的深度=%d
", isEmpty(T), getBiTreeDepth(T));
// 获得二叉树的根
ElemType e = getRoot(T);
printf("二叉树的根为: %c
", e);
// 遍历二叉树
printf("
前序遍历二叉树:");
preOrderTraverse(T);
printf("
中序遍历二叉树:");
inOrderTraverse(T);
printf("
后序遍历二叉树:");
postOrderTraverse(T);
printf("
");
// 销毁二叉树
destroyBiTree(&T);
printf("
销毁二叉树后,树空否?%d(1:是 0:否) 树的深度=%d
", isEmpty(T), getBiTreeDepth(T));
return 0;
}
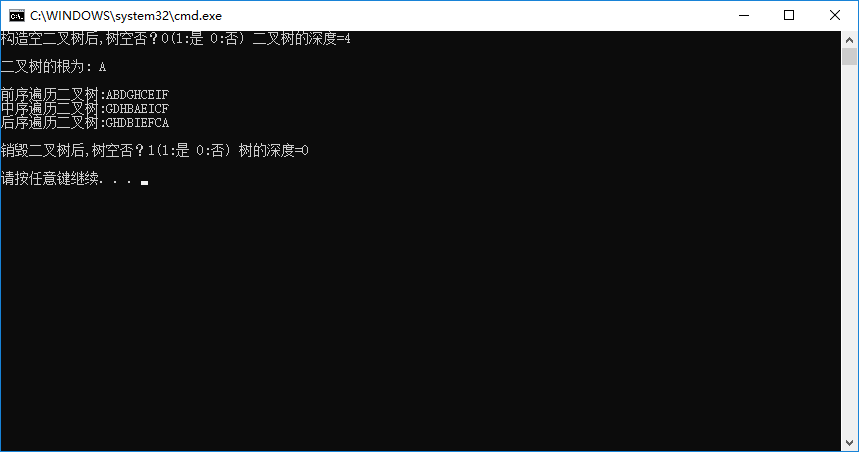
输出结果如下图所示:
参考:
《大话数据结构 - 第6章》 树