[数据结构

线性表是数据结构中最常用和最简单的一种结构。

一、线性表的定义

线性表，从名字上你就能感觉到，是具有像线一样的性质的表。例如一个班级的小朋友，一个跟着一个排着队，有一个打头，有一个收尾，当中的小朋友每一个都知道他前面一个是谁，他后面一个是谁，这样如同有一根线把他们串联起来了，就可以称之为线性表。

线性表：零个或多个数据元素的有限序列。

线性表的几个关键点：

• 它是一个序列，元素之间是有个先来后到的顺序。
• 若元素存在多个，则第一个元素无前驱，而最后一个元素无后继，其他元素都有且只有一个前驱和后继。
• 线性表强调是有限的。

若将线性表记为 (a₁，…，a_i-1, a_i, a_i+1, …, a_n)，则表中 a_i-1 领先于a_i，称 a_i-1 是 a_i 的直接前驱元素，a_i+1 是 a_i 的直接后继元素。当 i=1, 2,…, n-1 时，a_i 有旦仅有一个直接后继，当 i=2,3,…, n 时， a_i 有且仅有一个直接前驱。如下图所示：

所以线性表元素的个数 n(n>0) 定义为线性表的长度，当 n=0 时，称为空表。

在非空表中的每个数据元素都有一个确定的位置，如 a_i 是第一个数据元素，a_n 是最后一个数据元素，a_i 是第 i 个数据元素，称 i 为数据元素 a_i 在线性表中的位序。

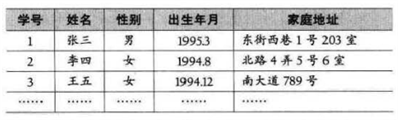
公司的组织架构，总经理管理几个总监，每个总监管理几个经理，每个经理都有各自的下属和员工。这样的组织架构是不是线性关系呢？
不是，为什么不是呢?哦，因为每一个元素，都有不只一个后继， 所以它不是线性表。

班级同学的点名册，是不是线性表？
是，这和刚才的友谊关系是完全不同了，因为它是有限序列，也满足类型相同的特点。这个点名册(如下表所示)中，每一个元素除学生的学号外，还可以有同学的姓名、性别、出生年月什么的，这其实就是我们之前讲的数据项。

在较复杂的线性表中， 一个数据元素可以由若干个数据项组成。

二、线性表的抽象数据类型

前面我们已经给了线性表的定义，现在我们来分析一下，线性表应该有一些什么样的操作呢

假设老师为了让小朋友有秩序地出入，所以就考虑给他们排一个队，并且是长期使用的顺序，这个考虑和安排的过程其实就是一个线性表的创建和初始化过程。

一开始没经验，把小朋友排好队后， 发现有的高有的矮，队伍很难看，于是就让小朋友解散重新排 - 这是一个线性表清空重置的操作。

排好了队，我们随时可以叫出队伍某一位置的小朋友名字及他的具体情况。这种可以根据位序得到数据元素也是一种很重要的线性表操作。

有时我们想知道，某个小朋友，比如麦兜是否是班里的小朋友。这种查找某个元素是否存在的操作很常用。

而后有家长问老师，班里现在到底有多少个小朋友呀，这种获得线性表长度的问题也很普遍。

对于一个幼儿园来说，加入一个新的小朋友到队列中，或因某个小朋友生病，需要移除某个位置，都是很正常的情况。对于一个线性表来说，插入数据和删除数据都是必须的操作。

所以，线性表的抽象数据类型定义如下:

ADT    线性表（List)
Data
        /*线性表的数据对象集合为{a1,a2,……an}，每个元素的类型均为DataType。其中，除第一个元素a1外，每一个元素有且只有一个直接前驱元素，除了最后一个元素an外，每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。*/
Operation
        initList(*L):    //初始化操作，建立一个空的线性表L。
        listEmpty(L):    //若线性表为空，返回true，否则返回false。
        clearList(*L):    //将线性表清空。
        getElem(L, i, *e):    //将线性表L中的第i个位置元素值返回给e。
        locateElem(L, e):    //在线性表L中查找与给定值e相等的元素。
        listInsert(*L, i, e):    //在线性表L中的第i个位置插入新元素e。
        listDelete(*L, i, *e):    //删除线性表L中第i个位置元素，并用e返回其值。
        listLength(L):    //返回线性表L的元素个数。
endADT

对于不同的应用，线性表的基本操作是不同的，上述操作是最基本的，对于实际问题中涉及的关于线性表的更复杂操作，完全可以用这些基本操作的组合来实现。

实现线性表的并集操作

比如，要实现两个线性表集合 A 和 B 的并集操作。即要使得集合 A=AUB。 说白了，就是把存在集合 B 中但并不存在 A 中的数据元素插入到 A 中即可。

仔细分析一下这个操作，发现我们只要循环集合 B 中的每个元素，判断当前元素是否存在 A 中，若不存在，则插入到 A 中即可。 思路应该是很容易想到的。

我们假设 La 表示集合 A， Lb 表示集合 B，则实现的代码如下:

void union(List *La, list *Lb)
{
    int La_len, Lb_len, i;
    ElemType e; 			 /* 声明与La和Lb相同的数据元素 e */
    La_len = listLength(La); /* 求线性表的长度 */
    Lb_len = list_length(Lb);
    for(i=1; i<=Lb_len; i++)
    {
        getElem(Lb, i, e); /* 取Lb中第i个数据元素给e */
        if(!locateElem(La, e, equal)) /* La中不存在和e相同的数据元素 */
            listInsert(La, ++La_len, e); /* 插入 */
    }
}    

这里，我们对于 union 操作，用到了前面线性表基本操作 ListLength、GetElem、
LocateElem、 Listlnsert 等，可见，对于复杂的个性化的操作，其实就是把基本操作组合起来实现的。

三、线性表的存储结构

线性表有两种物理存储结构：顺序存储结构和链式存储结构。下面就分别介绍一下。

3.1 顺序存储结构

线性表的顺序存储结构：用一段地址连续的存储单元依次存储线性表的数据元素，比如数组。

顺序存储结构的优缺点：

在存、读数据时，不管是哪个位置，时间复杂度都是 O(1)。而插入或删除时，时间复杂度都是 O(n)。这说明，它比较适合元素个数比较稳定，不经常插入和删除元素，更多的操作是存取数据的应用。

优点：

1. 无须为表中元素之间的逻辑关系而增加额外的存储空间（和链式存储比较而言）。
2. <可以快速地存取表中任意位置的元素。

缺点：

1. 插入和删除操作需要移动大量元素。
2. 当线性表长度变化较大时，难以确定存储空间的容量。
3. 容易造成存储空间的碎片。

应用：

使用顺序存储结构的线性表即为顺序线性表，分为静态和动态（不常用）两种。

3.2 链式存储结构

前面我们讲的线性表的顺序存储结构。它是有缺点的，最大的缺点就是插入和删除时需要移动大量元素，这显然就需要耗费时间。能不能想办法解决呢?

这就要使用线性表的链式存储结构了，即链表，其特点是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的。

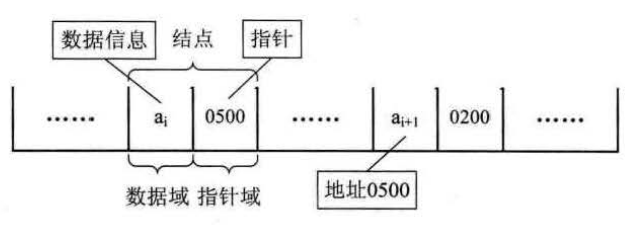
链式结构中，为了表示每个数据元素 a_i 与其直接后继数据元素 a_i+1 之间的逻辑关系， 对数据元素 a_i 来说， 除了存储其本身的信息之外，还需存储一个指示其直接后继的信息
(即直接后继的存储位置)。我们把存储数据元素信息的域称为数据域， 把存储直接后继位置的域称为指针域。这两部分信息组成数据元素 a_i 的存储映像，称为结点(Node)。

n 个结点(a_i 的存储映像) 链结成一个链表，即为线性表(a₁， a₂,…, a_n) 的链式存储结构，因为此链表的每个结点中只包含一个指针域，所以叫做单链表。单链表正是通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起，如下图所示：

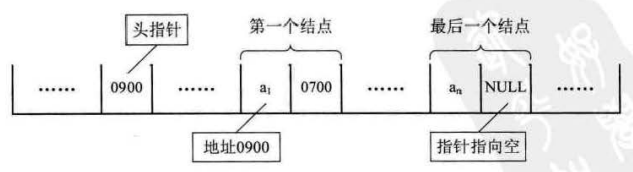
我们把链表中第一个结点的存储位置叫做头指针，那么整个链表的存取就必须是从头指针开始进行了。之后的每一个结点，其实就是上一个的后继指针指向的位置。想象一下，最后一个结点，它的指针指向哪里?
最后一个，当然就意味着直接后继不存在了，所以我们规定，线性链表的最后一个结点后继指针指向空，如下图所示：

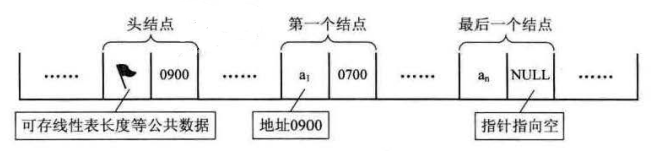
有时，我们为了更加方便地对链装进行操作，会在单链表的第一个结点前附设一个结点，称为头结点。头结点的数据域可以不存储任何信息，也可以存储如线性表的长度等附加信息，头结点的指针域存储指向第一个结点的指针，如下图所示：

3.3 头指针与头结点的异同点

头指针与头结点的异同点，如下图所示：

参考：

《大话数据结构 - 第3章》 线性表