题目1
标题:分数
1/1 + 1/2 + 1/4 + 1/8 + 1/16 + ....
每项是前一项的一半,如果一共有20项,
求这个和是多少,结果用分数表示出来。
类似:
3/2
当然,这只是加了前2项而已。分子分母要求互质。
注意:
需要提交的是已经约分过的分数,中间任何位置不能含有空格。
请不要填写任何多余的文字或符号。
解题思路:可直接手算通分,利用cmath里的pow()函数,很容易得出答案
答案:1048575/524288
题目2
标题:星期一
整个20世纪(1901年1月1日至2000年12月31日之间),一共有多少个星期一?
(不要告诉我你不知道今天是星期几)
注意:需要提交的只是一个整数,不要填写任何多余的内容或说明文字。
解题思路:算出1901年第一天开始到2000年最后一天的总天数sum(注意闰年的判断),
易得出sum=36525(天);由于2000年12月31日是周日,按照周日,六,五,四,三,
二,一的顺序往前推,共有36525/7=5217 个循环,余数是6. 故可知这六个数分别对应
的是前六项(不含周一)
因此答案应为:5217
题目3
标题:乘积尾零
如下的10行数据,每行有10个整数,请你求出它们的乘积的末尾有多少个零?
5650 4542 3554 473 946 4114 3871 9073 90 4329
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899
1486 5722 3135 1170 4014 5510 5120 729 2880 9019
2049 698 4582 4346 4427 646 9742 7340 1230 7683
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649
6701 6645 1671 5978 2704 9926 295 3125 3878 6785
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074
689 5510 8243 6114 337 4096 8199 7313 3685 211
注意:需要提交的是一个整数,表示末尾零的个数。不要填写任何多余内容
思路:两个数乘积结果产生0的情况只有两种:
(1)这两个数的因子分别应含有2和5
(2)某一个乘数本身含有尾零
#include<iostream>
using namespace std;
int main()
{
int num_2=0;//含有因子2的个数
int num_5=0;//含有因子5的个数
int a[10][10]={
{5650,4542,3554,473, 946, 4114, 3871, 9073, 90, 4329},
{2758 ,7949, 6113,5659, 5245, 7432, 3051, 4434, 6704, 3594},
{9937 ,1173 ,6866,3397 ,4759, 7557, 3070, 2287, 1453, 9899},
{1486 ,5722 ,3135,1170, 4014, 5510, 5120, 729, 2880, 9019},
{2049 ,698 ,4582,4346 ,4427, 646, 9742, 7340, 1230, 7683},
{5693 ,7015 ,6887,7381, 4172, 4341, 2909, 2027, 7355, 5649},
{6701 ,6645 ,1671,5978 ,2704, 9926, 295, 3125, 3878, 6785},
{2066,4247 ,4800,1578, 6652, 4616, 1113, 6205, 3264, 2915},
{3966,5291 ,2904,1285, 2193, 1428, 2265, 8730, 9436, 7074},
{689,5510,8243,6114, 337, 4096, 8199, 7313, 3685, 211}
} ;
int sum=0;
for(int i=0;i<10;i++)
{
for(int j=0;j<10;j++)
{
while(a[i][j]%10==0)
{
sum++;a[i][j]/=10;//含有末尾0的话,sum直接+1;
}
while(a[i][j]%2==0)
{
num_2++;a[i][j]/=2;
}
while(a[i][j]%5==0)
{
num_5++;a[i][j]/=5;
}
}
}
cout<<sum+((num_2<num_5)?num_2:num_5)<<endl;
return 0;
}
答案:31
题目4
标题:第几个幸运数
到x星球旅行的游客都被发给一个整数,作为游客编号。
x星的国王有个怪癖,他只喜欢数字3,5和7。
国王规定,游客的编号如果只含有因子:3,5,7,就可以获得一份奖品。
我们来看前10个幸运数字是:
3 5 7 9 15 21 25 27 35 45
因而第11个幸运数字是:49
小明领到了一个幸运数字 59084709587505,他去领奖的时候,人家要求他准确地说出这是第几个幸运数字,否则领不到奖品。
请你帮小明计算一下,59084709587505是第几个幸运数字。
需要提交的是一个整数,请不要填写任何多余内容。
解题思路:用一个队列装幸运数,从3,5,7出发,依次将队首乘3,5,7的结果加入队尾(注意判重),直到出现目标59084709587505.
程序代码如下:
#include<iostream>
#include<string.h>
#include<algorithm>
using namespace std;
long long q[10000];int mul[3]={3,5,7};
int main()
{
memset(q,sizeof(q),0);
q[0]=3;q[1]=5;q[2]=7;
int front=0;int rear=3;
while(front<rear)
{
for(int i=0;i<3;i++)
{
if(q[front]*mul[i]>59084709587505)continue;//大于59084709587505的排在后面的不入队列
long long t=q[front]*mul[i];
bool exist=0;
for(int j=rear-1;j>=0;j--)if(q[j]==t){exist=1;break;}//判断t是否已经在队列中
if(!exist)
{
q[rear]=t;rear++;//将t入队
if(t==59084709587505)//此时队尾元素已经是59084709587505,但还存在front到rear之间的元素和3,5,7相乘的结果小于59084709587505的可能
{
for(int k=front;k<rear-1;k++)//以上<59084709587505的可能情况,都应加入队列中
{
for(int i=0;i<3;i++)
{
long long t=q[k]*mul[i];
if(t<59084709587505)
{
bool exist=0;
for(int j=rear-1;j>=0;j--)if(q[j]==t){exist=1;break;}//判断t是否已经在队列中
if(!exist)
{
q[rear]=t;rear++;
}
}
}
}
sort(q,q+rear);//对3到59084709587505的幸运数进行排序
int pos=rear-1;
while(q[pos]!=59084709587505)pos--;//查找排序后的59084709587505所在的下标序号
cout<<pos+1<<endl;return 0;
}
}
}
front++;
}
return 0;
}
运行结果:1905
题目5
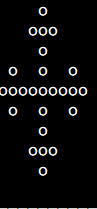
标题:打印图形
如下的程序会在控制台绘制分形图(就是整体与局部自相似的图形)。
当n=1,2,3的时候,输出如下:
请仔细分析程序,并填写划线部分缺少的代码。
n=1时:
n=2时:
n=3时:
源程序:
#include <stdio.h>
#include <stdlib.h>
void show(char* buf, int w){
int i,j;
for(i=0; i<w; i++){
for(j=0; j<w; j++){
printf("%c", buf[i*w+j]==0? ' ' : 'o');
}
printf("
");
}
}
void draw(char* buf, int w, int x, int y, int size){
if(size==1){
buf[y*w+x] = 1;
return;
}
int n = _________________________ ; //填空
draw(buf, w, x, y, n);
draw(buf, w, x-n, y ,n);
draw(buf, w, x+n, y ,n);
draw(buf, w, x, y-n ,n);
draw(buf, w, x, y+n ,n);
}
int main()
{
int N = 3;
int t = 1;
int i;
for(i=0; i<N; i++) t *= 3;
char* buf = (char*)malloc(t*t);
for(i=0; i<t*t; i++) buf[i] = 0;
draw(buf, t, t/2, t/2, t);
show(buf, t);
free(buf);
return 0;
}
注意:只提交划线部分缺少的代码,不要抄写任何已经存在的代码或符号。
解题思路:此题较简单。直接上答案: size/3