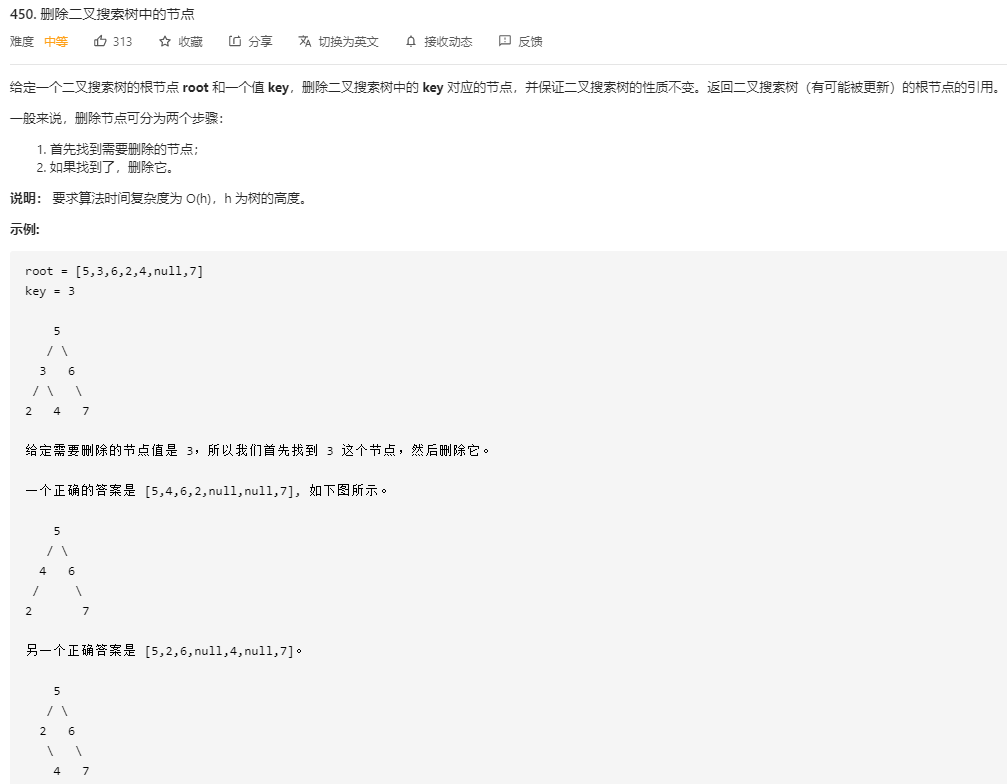
删除一个二叉搜索树中的节点,需要进行情况的分类讨论,看一下将这个节点删除之后是否需要对二叉搜索树进行调整(为了保持树的连接和维持二叉搜索树的性质)。
(1)如果删除的是一个叶子节点,那问题不大,因为它没有左子树和右子树,直接返回NULL就行了,表示它没了。
(2)如果要删除的节点,左右子树都存在,那麻烦了,删除这个节点是需要进行调整的,删除的这个节点可以用它左子树的最大值或者右子树的最小值来替代(为了
维持二叉搜索树的性质),这里我们用右子树的最小值来代替这个被删除的最小值。然后递归地到右子树删除那个原来右子树中的最小值(因为它已经滚到那个被删除的节点上了)。
(3)如果要删除的节点左子树不存在,那我们直接让这个被删除的节点的父节点的右指针指向被删除节点的右孩子就好了。也就是跳过了这个被删除的节点,表示这个节点被删除了。
这一步操作直接用root = root -> right;就可以完成。
(4)如果被删除的节点右子树不存在,那就类似(3),直接用root = root -> left;表示将被删除的节点的父节点的左指针指向被删除节点的左孩子,表示将这个节点删除。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* findSmallest(TreeNode* root) { // 找到以root为根的树中的最小值,这个函数是为了在删除某个节点且这个节点右子树不为空时,找到右子树中的最小值
if(root == NULL) {
return NULL;
} else if(root -> left != NULL) { // 如果左子树不为空,这最小值在左子树中,递归地去左子树中寻找最小值
return findSmallest(root -> left);
}
return root; // 如果左子树为空,这最小值就是root,这是由二叉搜索树的性质决定的
}
TreeNode* deleteNode(TreeNode* root, int key) {
if(root == NULL) {
return NULL;
} else if(key < root -> val) { // 要删除的值小于根节点的值,递归地到左子树中删除这个节点
root -> left = deleteNode(root -> left, key);
} else if(key > root -> val) { // 要删除的值大于根节点的值,递归地到右子树中删除这个节点
root -> right = deleteNode(root -> right, key);
} else {
if(root -> left == NULL && root -> right == NULL) { // 如果被删除的节点是叶节点,直接删除这个节点,返回NULL即可
return NULL;
} else if(root -> left != NULL && root -> right != NULL) { // 如果被删除的节点左、右子树都不为空
TreeNode* temp = findSmallest(root -> right); // 那就找到右子树中最小的值(也就是被删除的节点的中序后继),用这个节点代替被删除的节点
root -> val = temp -> val;
root -> right = deleteNode(root -> right, root -> val); // 然后递归地到右子树中删除这个节点
} else if(root -> left != NULL) { // 如果左子树不为空,这直接连接被删除的节点的父节点的左指针到这个左子树上
root = root -> left;
} else if(root -> right != NULL) { // 右子树不为空时同理
root = root -> right;
}
}
return root;
}
};