LeetCode第202场周赛

第一题 5185. 存在连续三个奇数的数组

class Solution {
public:
    bool threeConsecutiveOdds(vector<int>& arr) {
        int size = arr.size();
        for(int i = 0; i + 2 < size; ++i) {
            if(arr[i] % 2 == 1 && arr[i + 1] % 2 == 1 && arr[i + 2] % 2 == 1) {
                return true;
            }
        }
        return false;
    }
};

第二题 5488. 使数组中所有元素相等的最小操作数

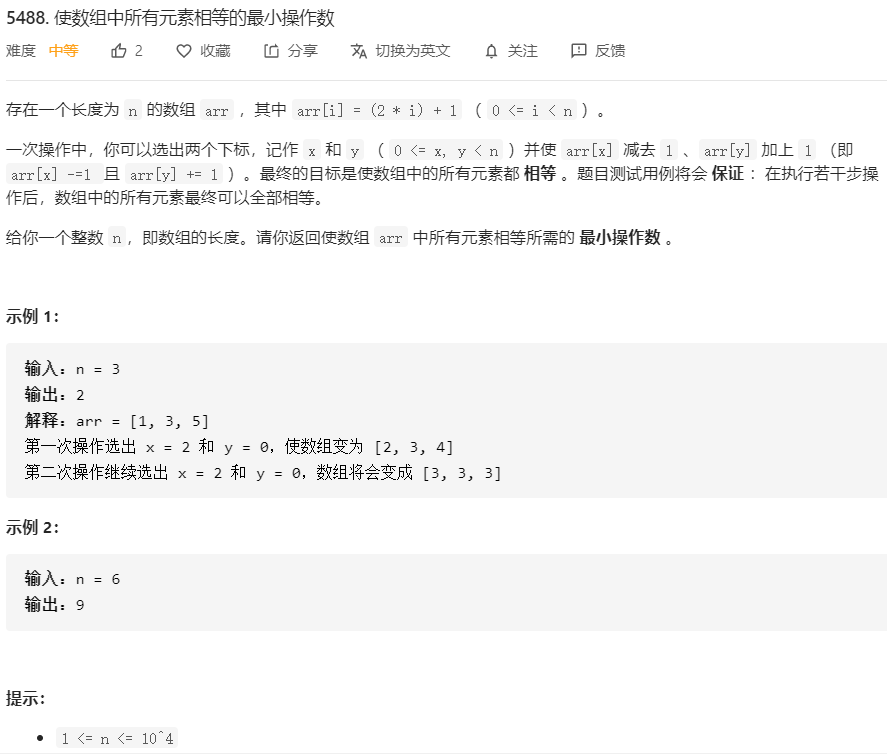
用等差数列求和公式计算一下就知道，不管n为多少，所有数的和都是n^2，这样平均数就是n，由于数组前半部分和后半部分关于n对称（关于中间位置对称的两个位置的
两个元素相加和为2*n)，所以我们只需要遍历数组的前半部分，把所有数和n的差值加起来，就是最终的答案了。

class Solution {
public:
    int minOperations(int n) {
        int res = 0;
        for(int i = 0; i < n / 2; ++i) {
            res += (n - (2 * i + 1));
        }
        return res;
    }
};

第三题 5489. 两球之间的磁力

首先，题目给的position数组可能是无序的，所以需要先对position数组排序，排序之后我们希望能够在所有篮子里放上m个球，让任意两个球
之间的最小距离最大。
由于position的最大范围到了1e9，所以我们如果从1开始逐个考虑增大最大距离来放球，就比较慢。
因为position范围大，所以我们可以考虑二分。

这里二分的是距离，也就是两个球之间的距离，假设现在二分到的距离为mid,因为第一个球肯定是放在最左边，所以我们遍历position数组，找到下一个距离大于
mid且离上一个球最近的篮子的position，在这里放一个球，然后再找下一个位置，就这样，如果遍历完数组之前能够放下所有的球，说明当前这个距离ok，我们就更新一下答案，
然后扩大mid，尝试两个球之前放远一点行不行。
如果某个距离mid使得遍历完position之后放不了m个球，说明距离太大了，我们需要减小距离（为了多放点球）。

由于需要多次判断某距离是否可以放下m个球，我们写一个check函数，判断在position数组中距离为dis时是否能放下m个球。

代码如下：

class Solution {
public:
    bool check(vector<int>& position, int m, int dis) {            //当前距离为dis,也就是说两个球之间的距离最小为dis
        int last = position[0];                  //第一个球放在最左边
        --m;                                     //剩余球的数量减一
        for(int i = 1; i < position.size() && m > 0; ++i) {
            if(position[i] - last >= dis) {            //找到了第一个和上个球的距离大于等于dis的篮子了
                last = position[i];                    //那就放一个球
                --m;                                   //剩余球的数量减一
            }
        }
        return m == 0;                                 //剩余球的数量为0，说明放满了m个球，说明最小距离为dis是ok的
    }

    int maxDistance(vector<int>& position, int m) {
        sort(position.begin(), position.end());
        int left = 0, right = 1e9 + 5;
        int res = 0;
        while(left < right) {                              //二分找出最小距离的最大值
            int mid = (left + right + 1) >> 1;
            if(check(position, m, mid) == true) {          //如果当前距离ok，可以考虑加大距离
                res = max(res, mid);
                left = mid;
            } else {                  
                right = mid - 1;
            }
        }
        return res;
    }
};

第四题 5490. 吃掉 N 个橘子的最少天数

每天都有可能有三种操作：（1）吃掉一个橘子; （2）如果当前橘子的数量是偶数的话，可以吃掉一半的橘子；
（3）如果当前橘子的数量是三的倍数的话，可以吃掉三分之二的橘子。

由于对于每个数量，都需要用到比它较小的几个数量的值，所以我们很容易想到记忆化搜索。以及递推计算每个数量的橘子
对应的天数。

由于每一天都可以吃掉一个橘子，所以理论上我们每天都会递推到前一天的状态，这样，我们记忆化搜索开的状态数组实际上就是O(n)的，
由于这题数据范围最大可以到2e9,因此这个空间开销还是太大了。

我们需要想办法优化递推方式。
可以这么想，对于一个较大的数，假设我们只可以进行前两个操作（1）吃掉一个橘子; （2）如果当前橘子的数量是偶数的话，可以吃掉一半的橘子。
那么，如果我们当前不能直接吃掉一半（橘子数量不是偶数），我们也希望吃掉一个橘子之后马上就吃掉一半橘子，而不是一个一个吃掉。
所以实际上，我们不需要一个一个往下算，减一操作到当前橘子数量是偶数就可以了。

同理，如果我们能让当前橘子数量除以3，我们也希望能在进行几次“吃掉一个橘子”的操作之后让橘子的数量达到3的倍数。
这样也能减小减一操作的次数，更重要的是，优化了空间。

同样的，由于经常进行除2和除3操作，所以我们没有必要存储太多的状态，只需要存储一些常用的，因此我们可以考虑用一个哈希表unordered_map来存储
每个数量的橘子对应的天数，这样，我们没有计算到的橘子数量，就没必要存储天数了，这进一步优化了空间。

代码如下：

class Solution {
public:
    unordered_map<int, int> dp;            //key是橘子数量，value是对应的天数

    int getDays(int n) {
        if(n == 1) {                        //递推边界
            return 1;
        }
        if(n == 2 || n == 3) {
            return 2;
        }
        auto it = dp.find(n);               
        if(it != dp.end()) {               //如果当前橘子数量对应的天数之前已经计算过了，直接查就好了，不用再算了
            return it -> second;
        }
        dp[n] = min(getDays(n / 2) + 1 + (n % 2), getDays(n / 3) + 1 + (n % 3));    //+1是因为除2或除3需要一天时间，(n % 2)和(n % 3）是让当前天数变为2或3的倍数需要“减一”的天数
        return dp[n];
    }
    
    int minDays(int n) {
        dp.clear();
        return getDays(n);
    }
};