LeetCode201. 数字范围按位与

暴力做法是，枚举从m~n的所有数，因为题目说了数据最大为2147483647，所以可以枚举0～30位，对所有数字的每一位做与运算。

数据比较大的时候这样做会超时（时间复杂度是O(n)）。

参考官方题解，有一个简单得多的做法。

观察发现，要对所有数做按位与，只要有一个数的某一位为0，则最后按位与的结果在这一位肯定也是0。

比如9, 10, 11, 12四个数做按位与，低三位各有一个数在那个位为0，因此最终按位与的结果在低三位肯定也是0，只有倒数第四位，四个数都是1，因此按位与的结果是1，所以最终所有数按位与的结果在倒数第四位也是1。
更高位的数就都是0了，没什么好说的。

可以发现，按位与的结果就是所有数的二进制公共前缀，低位全部是0.比如上面例子中公共前缀是倒数第四位的1，低三位都是0，所以结果就是1 0 0 0，也就是8.

因为从m到n，每一个数是逐渐加一的，每次加一，会从低位开始变化，所以所有数的公共前缀，就是左右端点m和n的公共前缀，所以我们只需要找到m和n的公共前缀，然后低位都补上0就可以了。

找公共前缀的方法可以用右移操作，同时右移m和n直到两个数相等，当然要记录位移的次数，然后把m（或n，此时m和n两个数已经相等了，就是他们的公共前缀）左移他们的位移次数（也就相当于低位补0）就是最后的答案了。

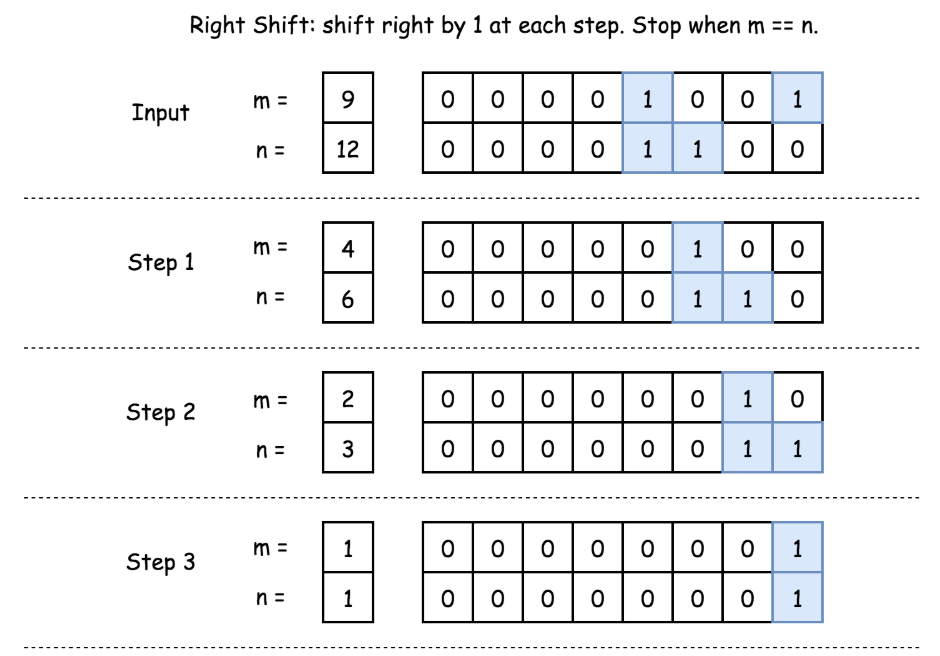
比如上图，9和12右移3次之后相等了，也就是找到公共前缀1，然后把1左移三次，就是9~12之间所有的数的按位与的结果了。

代码如下：

class Solution {
public:
    int rangeBitwiseAnd(int m, int n) {
        int shift = 0;                  //记录右移次数
        while(m < n) {                  //m和n同时右移，直到两个数相等（也就是找到了公共前缀）
            m >>= 1;
            n >>= 1;
            ++shift;
        }
        return m << shift;              //退出while循环后，m和n就是公共前缀了，左移shift次就是答案
    }
};