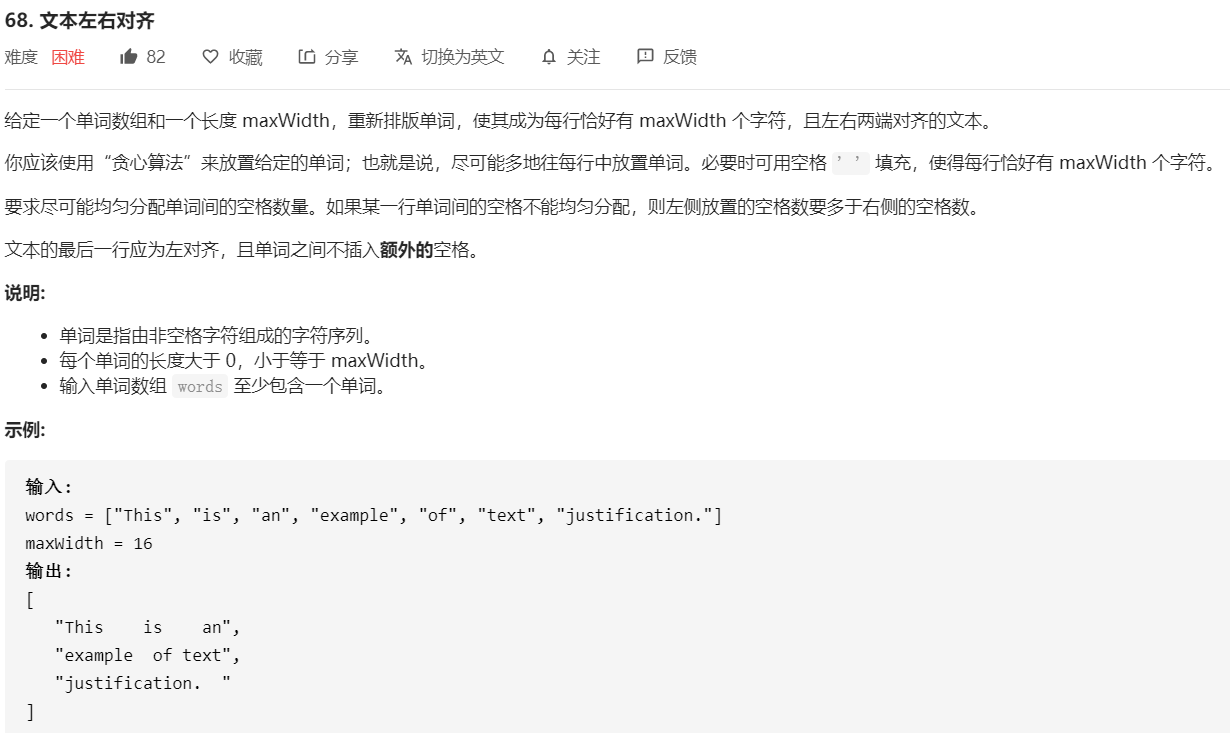

这题是一道模拟题,需要我们模拟word等文本编辑器都有的一个文本自动对齐功能。
从测试样例可以看出,文本对齐有三种情况需要判断:
1. 如果某行只含有一个字符串,这时只需要左对齐。比如某行可以放下100个字符,某单词长度98个字符,
这时不需要把这个单词左右对齐,让单词居中左右各一个空格,实际上这种情况是左对齐,剩下的长度全部用空格填充;
2. 如果是最后一行,那么这一行也是左对齐。即最后一行的每个单词之间的间隙只有一个空格,如果这一行长度没满maxWidth,剩下的部分用空格填充。
3. 剩下的情况都是左右对齐,也就是这一行的最左和最右都是单词,空格只出现在两个单词之间。
显然这种情况的间隙数量就是这一行单词数量减一(因为间隙需要出现在两个单词之间),
左右对齐还需要保证所有空格尽量均匀地分布在所有间隙里,如果无法让所有间隙的空格数量相同,
则“靠左”的间隙中空格数量会比“靠右”的间隙空格数量多一。
举个例子:如果某行有4个单词,有11个空格,由于有4个单词,因此能得到间隙数量是3。
11个空格要尽量均匀分布到三个间隙中,11 / 3 = 3(向下取整),11 - 3 * 3 = 2,
剩下的两个空格就从左到右分配到较靠左的间隙中,因此最后三个间隙的空格数量分别是4, 4, 3。
即靠左的间隙空格数量比靠右的间隙空格数量多一。
代码基本思路是:
遍历一遍words数组,先计算每行中每两个单词之间只放一个空格能放下多少个。
遍历的过程就计算得到这一行可以存放的字符串的开始下标和结束下标,然后我们再判断这一行的对齐方式,
上面分析过了,如果这一行就一个字符串,或者结尾单词到了words数组的末尾(说明当前行是最后一行),则对齐方式是左对齐;其他情况就是右对齐。
然后需要根据对齐方式得到这一行最后存放的字符串了。
-
如果是左对齐,那就根据开始和结束下标把所有单词连接起来(单词之间要再存一个空格),这样字符串长度可能小于maxWidth,剩下的部分用空格填充;
-
如果是左右对齐,那就需要先计算间隙数量gapNum和空格数量spaceNum了,靠左的间隙中的空格数量要比靠右的间隙的空格数量多一。
靠左的部分就是[0, spaceNum % gapNum - 1]。比如spaceNum = 11, gapNum = 3,那么[0, 1] 就是靠左的部分,间隙数量为spaceNum / gapNum + 1 = 4个。
靠右的部分就是[spaceNum % gapNum, gapNum),比如这个例子里就是[2, 3) -> 左开右闭,所以右边部分只有2,即第三个间隙比前两个间隙少一个空格,空格数量为spaceNum / gapNum = 3个。这和我们上面分析右对齐的时候的计算相同。
来看看代码:
class Solution {
public:
vector<string> fullJustify(vector<string>& words, int maxWidth) {
vector<string> res;
for(int i = 0; i < words.size(); ++i) {
int len = words[i].size(); //len表示当前行的第一个单词的开始到当前行最后一个单词结尾的字符总数(包含两个单词中间的空格)
int j = i + 1;
while(j < words.size() && len + 1 + words[j].size() <= maxWidth) { //只要当前行能放下一个空格再加上下一个单词,就加进来,这里判断条件len + 1的“加一”是加上间隙中空格的长度
len += 1 + words[j].size();
++j; //这个while循环结束后就确定了当前行的字符串数组下标: [i, j - 1],也就是说words[i]....words[j - 1]都在一行
}
string thisLine; //thisLine存放这一行最终的字符串,计算结束后压入res数组
if(j == i + 1 || j == words.size()) { //两种情况的对齐方式是左对齐:这一行就一个单词或者这一行是最后一行 j == i + 1表示这一行就一个单词, j == words.size()说明words数组已经遍历到了末尾,所以当前行是最后一行。 这两种情况都是左对齐,因此写到一个if语句里。
thisLine += words[i]; //最左边肯定是words[i],先加上
for(int k = i + 1; k < j; ++k) {
thisLine += ' ' + words[k]; //左对齐:每两个单词之间只有一个空格
}
while(thisLine.size() < maxWidth) { //如果当前行长度不满maxWidth,后面部分用空格填充
thisLine += ' ';
}
} else { //其他情况都是左右对齐,需要对每个间隙的空格数量做计算
thisLine += words[i]; //左右对齐的情况中当前行的最左边也是words[i],先加上
int gapNum = j - i - 1, spaceNum = maxWidth - len + gapNum; //计算间隙数量gapNum和空格数量spaceNum, 当前行的单词在words中的下标是[i, j),因此单词数量是j - i,间隙数量gapNum是单词数量减一,所以是j - i - 1, 空格数量是maxWidth减去len再加上len中的空格数量(正好是gapNum,因为每两个单词之间正好是一个空格,这是在第一个while循环里计算得到的)
int k = 0; //k表示从i开始的第几个单词
while(k < spaceNum % gapNum) { //靠左的间隙,分配到的空格数量要比靠右的间隙的空格数量多一,数量为spaceNum / gapNum + 1
thisLine += string(spaceNum / gapNum + 1, ' ') + words[i + k + 1];
++k;
}
while(k < gapNum) { //靠右的间隙,分配到的空格数量要比靠左的间隙的空格数量少一个,数量为spaceNum / gapNum
thisLine += string(spaceNum / gapNum, ' ') + words[i + k + 1];
++k;
}
}
res.push_back(thisLine);
i = j - 1; //因为当前行的单词是第i ~ 第j - 1个,所以下一行需要从j开始计算,由于最外层的for循环会作一个加一操作(++i),所以这里给i赋值为j - 1
}
return res;
}
};