前面介绍的Stack是新进后出,而Queue是先进先出的
1、Queue结构
public interface Queue<E> extends Collection<E> {
boolean add(E e);
boolean offer(E e);
E remove();
E poll();
E element();
E peek();
}
Queue是一个接口。
2、PriorityQueue源码分析
PriorityQueue是一个优先队列,和先进先出的队列的区别是: 优先队列每次出队的元素都是优先级最高的元素。 如何确定哪一个元素的优先级呢? jdk中使用堆这种数据结构,通过堆使得每次出队的元素总是队列里最小的,而元素大小的比较可以通过Compareator指定,相当于优先级。
3、什么是堆和二叉堆?
1) 堆中某个节点的值总是不大于或者不小于其父节点的值
2) 堆总是一颗完全树
场景的堆有二叉堆、斐波那契堆等。而PriorityQueue是二叉堆。
二叉堆是一种特殊的堆,二叉堆是完全二叉树或者近似完全二叉树。二叉堆有两种:最大堆和最小堆
最大堆: 父节点的键值总是大于或等于任何一个子节点的键值
最小堆:父节点的键值总是小于或者等于任何一个子节点的键值
二叉堆图例
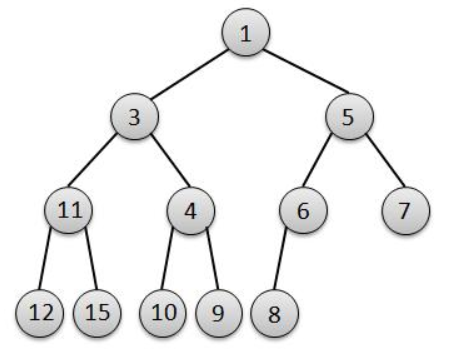
上图是一颗完全二叉树(二叉堆),特点是: 在第n层深度被填满之前,不会开始填第n+1层深度,而且元素插入是从左往右填满。
基于这个特点,二叉堆又可以用数组来表示而不是用链表。我们看一下下图用数组表示二叉堆
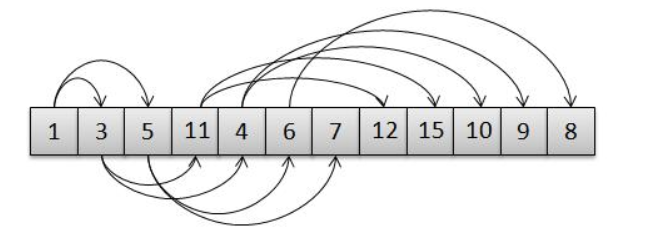
基于数组实现的二叉堆,对于数组中任意元素的n上元素,其左孩子在2n+1位置上,右孩子在2n+2位置上,它的父节点在(n-1)/2上,而根节点是0的位置上。
4、PriorityQueue的数据结构,就是堆
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
// 默认容量是11
private static final int DEFAULT_INITIAL_CAPACITY = 11;
//使用数组来存储元素
transient Object[] queue; // non-private to simplify nested class access
//队列元素大小
private int size = 0;
//通过这个比较器实现优先级队列
private final Comparator<? super E> comparator;
}
5、构造函数
我们看主要的构造函数
public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.queue = new Object[initialCapacity];
this.comparator = comparator;
}
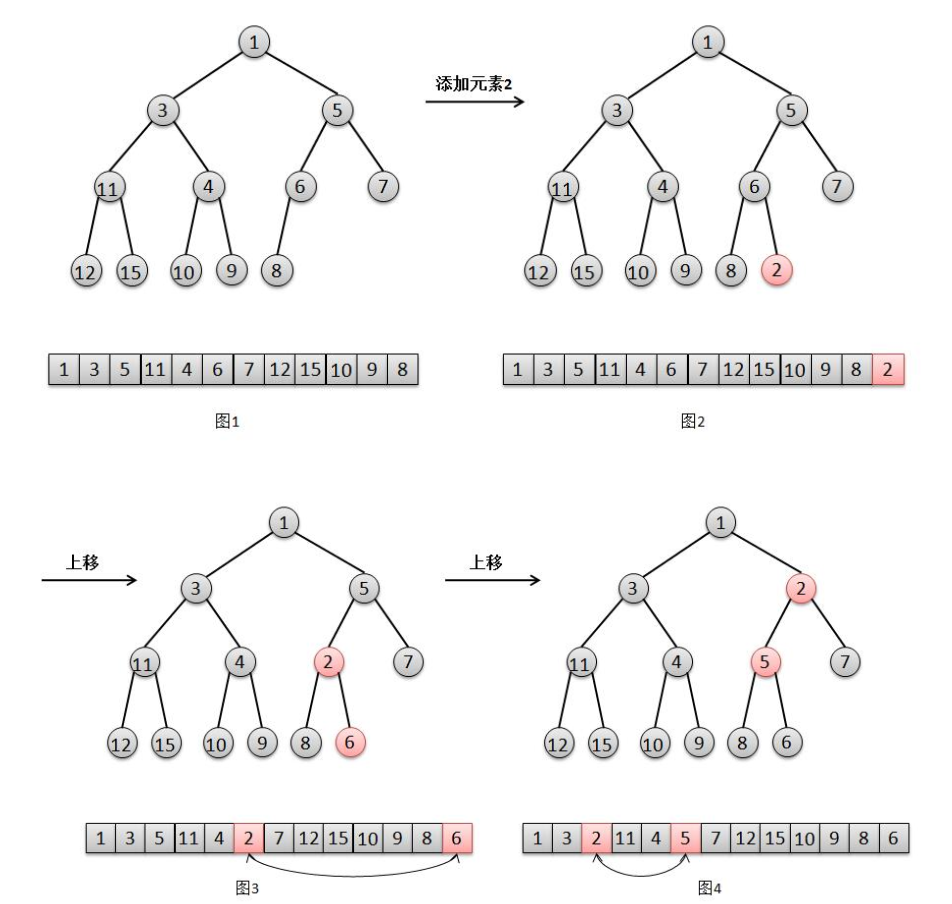
6、二叉堆的添加原理
二叉堆的特点:
1)父结点的键值总是小于或等于任何一个子节点的键值。
2)基于数组实现的二叉堆,对于数组中任意元素的n上元素,其左孩子在2n+1位置上,右孩子在2n+2位置上,它的父节点在(n-1)/2上,而根节点是0的位置上。
为了维护这个特点,二叉堆在添加元素的时候,需要一个“上移”的动作,如下图所示
7、添加元素源码解析
//添加一个元素
public boolean add(E e) {
return offer(e);
}
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
//修改版本+1
modCount++;
//记录当前队列元素的个数
int i = size;
//如果当前元素个数大于等于队列底层数组的长度,则进行扩容
if (i >= queue.length)
grow(i + 1);
//元素个数+1
size = i + 1;
//如果队列中没有元素,则将元素e直接添加到根
if (i == 0)
queue[0] = e;
//否则调用siftUp方法,将元素添加到尾部,进行上移判断
else
siftUp(i, e);
return true;
}
1) 扩容操作
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// 如果当前队列小于64,则扩容到2倍,否则扩容到1.5倍
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// 如果扩容后超出了int范围,则将newCapacity赋值为Integer.Max_VALUE
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
//数组copy进行扩容
queue = Arrays.copyOf(queue, newCapacity);
}
2)上移操作
//上移,x表示新插入元素,k表示新插入元素在数组中的位置
private void siftUp(int k, E x) {
//根据比较器是否为空,选择不同的上移操作方法
if (comparator != null)
siftUpUsingComparator(k, x);
else
siftUpComparable(k, x);
}
//比较器为空时,调用此方法进行上移操作
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
//k>0表示判断k不是根的情况下,也就是元素x有父节点。
while (k > 0) {
//计算元素x的父节点位置(n-1)/2
int parent = (k - 1) >>> 1;
//取出x的父元素e
Object e = queue[parent];
//如果新增的元素k比其父元素e大,则不需要“上移”,跳出循环结束
if (key.compareTo((E) e) >= 0)
break;
//x比父元素小,则需要进行“上移”
//交换元素x和父节点e的位置
queue[k] = e;
//将新插入元素位置k指向父节点位置,进行下一次循环
k = parent;
}
//找到新增元素x的合适位置k之后进行赋值
queue[k] = key;
}
总结: 二叉堆“上移”操作主要是不断的将新增的元素和父元素进行比较,比父节点小则上移。上移后再和父节点进行比较,直到根节点。
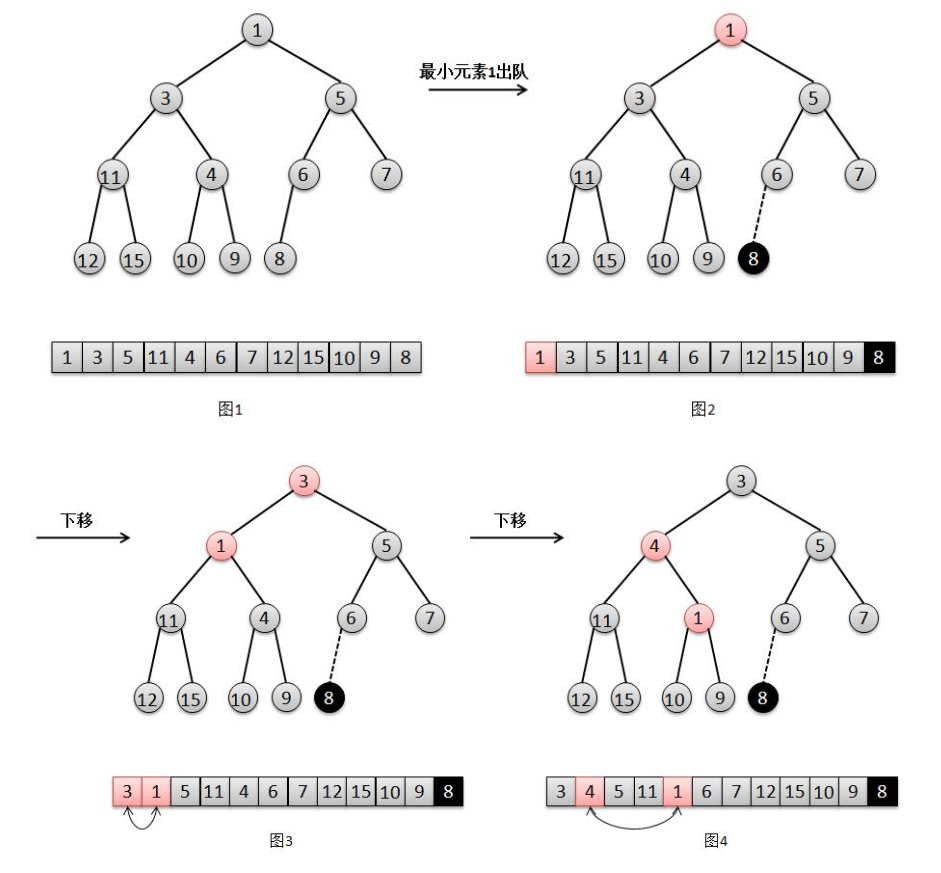
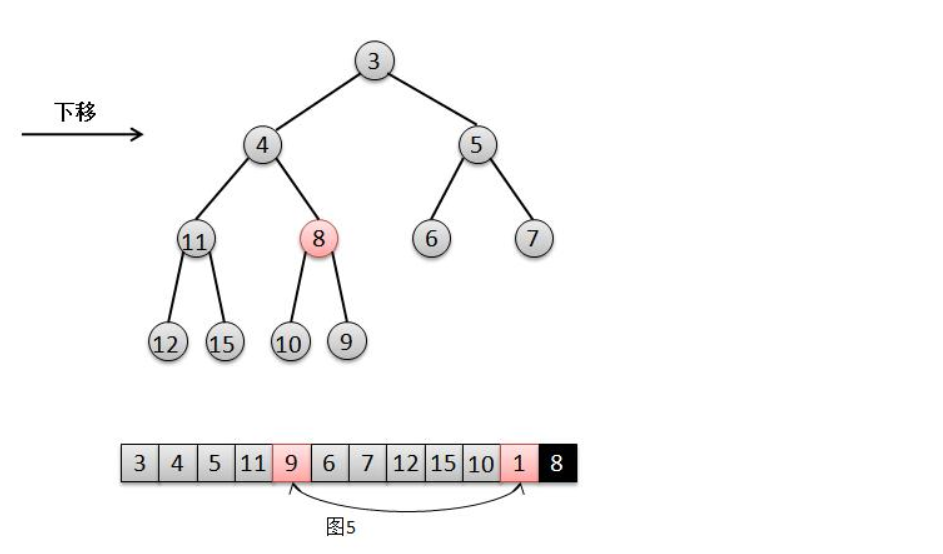
8、二叉堆删除原理
对应二叉堆出队操作,就是删除根元素,也就是最小的元素,找一个替代者移动到根位置,向对于被删除的元素来说就是“下移”