1.红黑树的根是黑的
2.所有外部节点[NIL]都是黑的
3.其余节点若为红则只能有黑孩子//红节点的儿子和父亲都是黑色的
4.外部节点到根途经的黑节点数目相等//黑深度
外部节点是一类本不存在的节点 引入是为了方便分析和实现
红黑树的局部结构无非四种
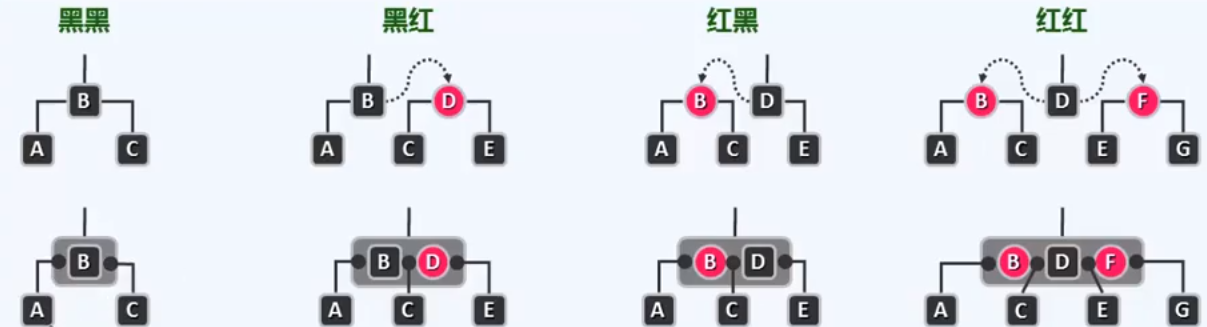
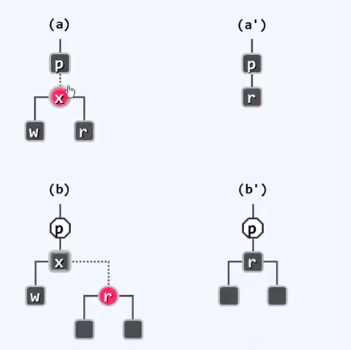
总是假设插入的节点是红色 除非是根
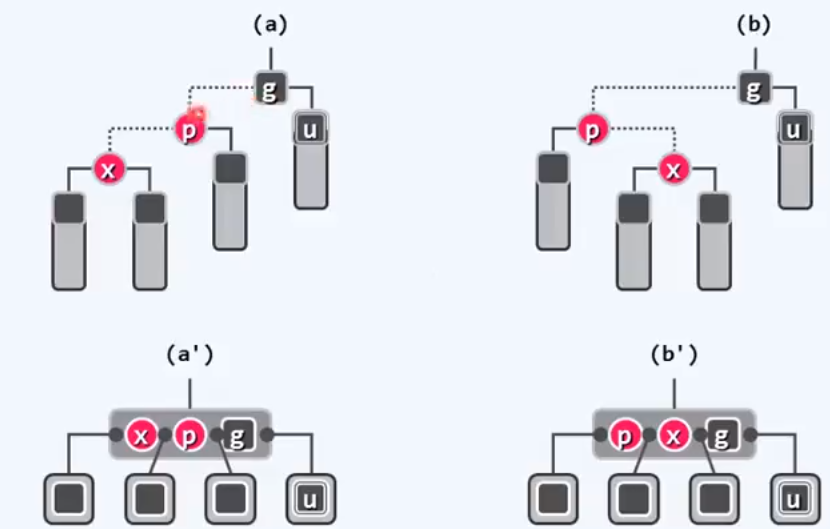
1.双红缺陷


情况1:叔父节点是黑色
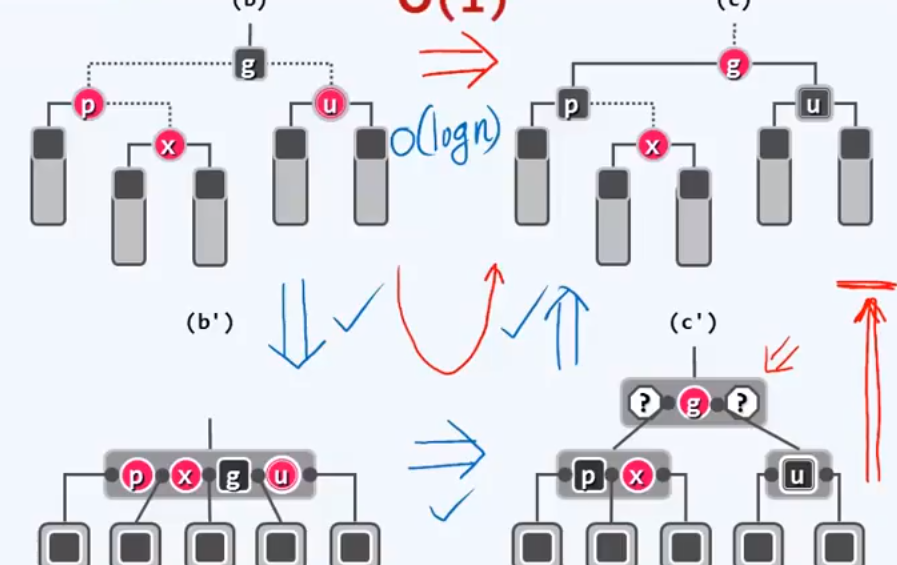
情况2:叔父节点是红色
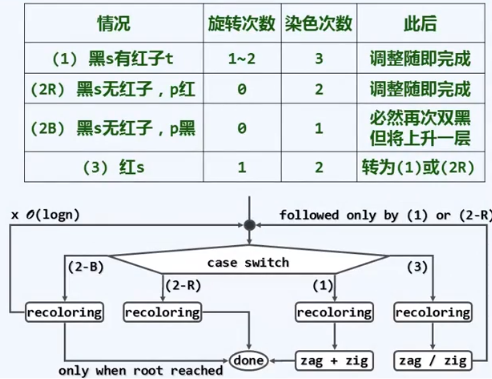
删除
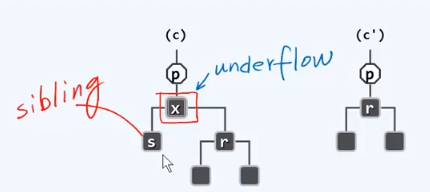
情况1:要删除的是红节点 红节点对黑高没有影响 或者删除的点是黑节点 但它至少有一个红儿子//x和它的儿子至少有一个是红的
双黑缺陷:x和它的儿子全是黑的 删除x后全树的黑深度不再统一
BB-1:x的兄弟节点s为黑 且s至少有一个红孩子t
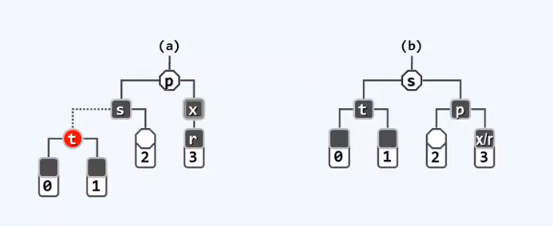
s直接继承p的颜色
BB-2R:x的兄弟s为黑 且s的两个孩子均为黑;p为红

BB-2B:x的兄弟s为黑 且s的两个孩子均为黑;p为黑
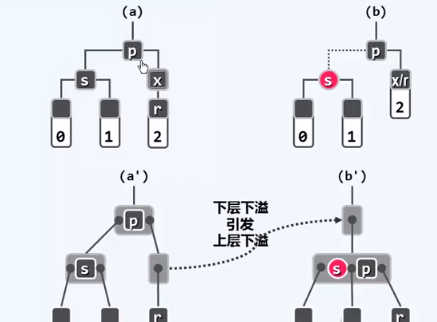
s染红相当于做合并
BB-3:x的兄弟s是红色 其余讨论节点均为黑
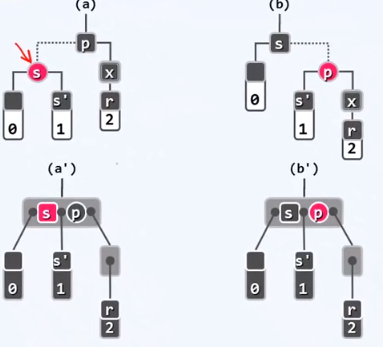
经过一次zig 或 zag s变黑 p变红 则此时情况转变为 x拥有一个黑兄弟s'的情况
既然p已经转红 那么只可能出现BB-1和BB-2R 因此我们不会连续出现下溢