(模板)AC自动机(简单版)
题目背景
这是一道简单的AC自动机模板题。
用于检测正确性以及算法常数。
为了防止卡OJ,在保证正确的基础上只有两组数据,请不要恶意提交。
提示:本题数据内有重复的单词,且重复单词应该计算多次,请各位注意
题目描述
给定(n)个模式串和(1)个文本串,求有多少个模式串在文本串里出现过。
输入格式
第一行一个(n),表示模式串个数;
下面(n)行每行一个模式串;
下面一行一个文本串。
输出格式
一个数表示答案
样例输入
2 a aa aa
样例输出
2
说明/提示
(subtask1)[(50pts)]:(sum length(模式串)<=10^6,length(文本串)<=10^6,n=1);
(subtask2)[(50pts)]:(sum length(模式串)<=10^6,length(文本串)<=10^6);
题解
AC自动机的板题,直接来讲AC自动机吧。
首先,字典树会吧,
其次,KMP会吧,
那么把这两个东西结合起来就是AC自动机了。
首先,我们根据输入的模式串建一棵字典树,
然后从根开始遍历这棵树,然后跑这棵树的KMP。
在KMP中,对于每一个点,我们需要求出(next),从头开始最长前缀等于以这个点为结尾的后缀(前缀长度小于开头到当前点的长度)。
但是对于AC自动机来说,这个前缀不一定是当前点的祖先,也有可能是其他子树的节点。
如下图:
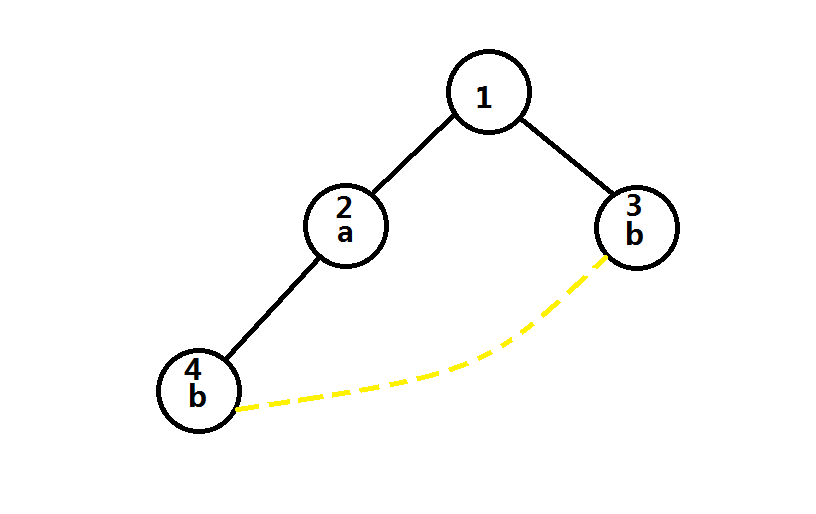
(4)号节点的(next)需要指向(3)号节点,
所以我们用一个很巧妙的方法解决这个问题,
只要用广搜来搜索这棵树就行了,
因为每个节点的(next)值所指向的点的深度一定是小于这个节点的,所以这个节点的(next)值所指向的点的(next)的值一定是求好了的(有点绕)。
然后我们按照KMP的算法求(next)值就好了。
接下来我们考虑一些小优化:
考虑到KMP求(next)值的时候经常会找到根节点,
那么我们就想到,要继续往上找(next)的条件是当前节点的(next)节点没有和将要搜索的字母相同的子节点,
那么当前节点的(next)节点的对应节点处应该是空着的,
那么我们如果用这个地方存这个节点所对应的(next)值(就是类似于这个地方连一条边到这个节点的(next)),那么后面求(next)找到这个地方的时候就可以直接放回需要的值了。
如下图:
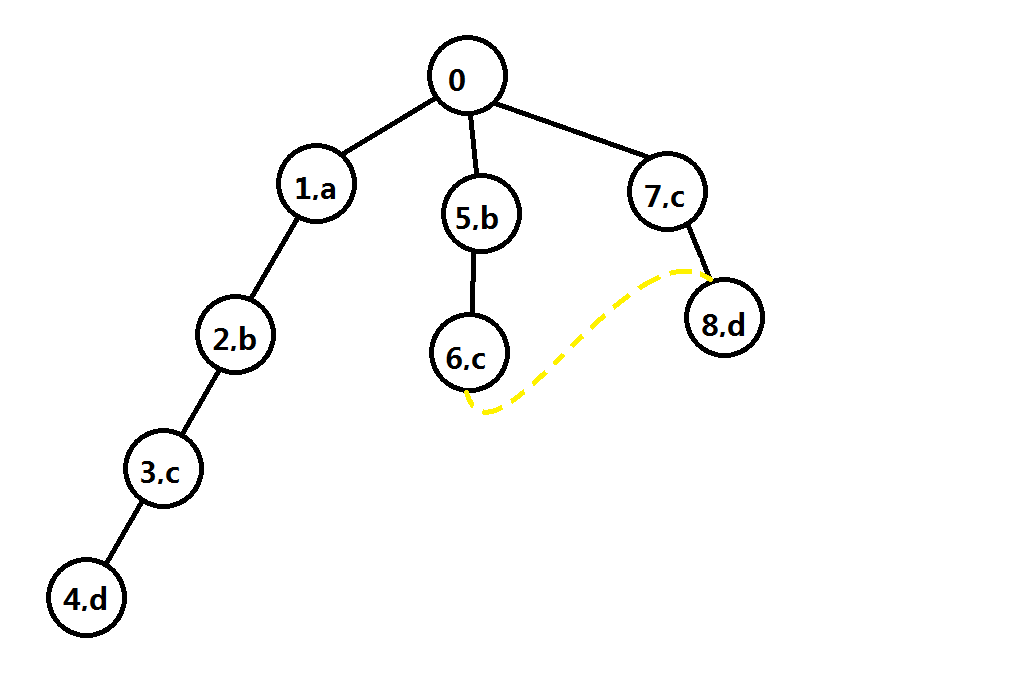
(6)号节点的(next)值指向(7),那么(6)号节点的("d")儿子就是(8)。
个人认为这个优化结合代码会好理解一点。
那么每次找(next)的时候时间复杂度就是(O(1))了。(只是一个常数级别的优化,也可以不加)
上代码:
#include<bits/stdc++.h>
using namespace std;
int n;
char c[1000009];
struct aa{
int s;
int up;
int to[30];
}p[1000009];
int len;
int ans;
void add(){
int l=strlen(c);
int u=0;
for(int j=0;j<l;j++){
if(p[u].to[c[j]-'a']) u=p[u].to[c[j]-'a'];
else {p[u].to[c[j]-'a']=++len;u=len;}
}
p[u].s++;
}
int q[1000009],l=1,r=0;
void bfs(){
for(int j=0;j<='z'-'a';j++)
if(p[0].to[j]) q[++r]=p[0].to[j];
while(l<=r){
int u=q[l++];
for(int j=0;j<='z'-'a';j++){
if(p[u].to[j]){
p[p[u].to[j]].up=p[p[u].up].to[j];
q[++r]=p[u].to[j];
}else p[u].to[j]=p[p[u].up].to[j];
}
}
}
int main(){
scanf("%d",&n);
for(int j=1;j<=n;j++){
scanf("%s",c);
add();
}
bfs();
scanf("%s",c);
int l=strlen(c);
int uu=0;
for(int j=0;j<l;j++){
uu=p[uu].to[c[j]-'a'];
int k=uu;
while(k && p[k].s!=-1){
ans+=p[k].s;
p[k].s=-1;
k=p[k].up;
}
}
printf("%d",ans);
return 0;
}