下文中的模型都是以Skip-gram模型为主。
1、论文发展
word2vec中的负采样(NEG)最初由 Mikolov在论文《Distributed Representations of Words and Phrases and their Compositionality》中首次提出来,是Noise-Contrastive Estimation(简写NCE,噪声对比估计)的简化版本。在论文中针对Skip-gram模型直接提出负采样的优化目标函数为:
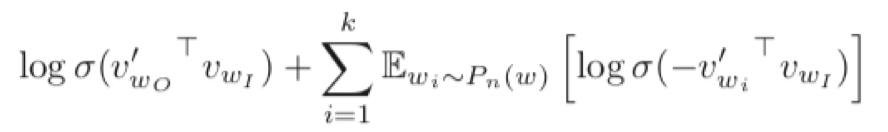
其中Pn(w)是目标词不是w的上下文的概率分布。
论文中没有给出证明,到了2014年,Yoav Goldberg在论文《word2vec Explained: Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method》里对上述目标函数给出了推导。
2、原始的skip-gram模型的目标函数
如果没有采用负采样的话,那么skip-gram模型的目标函数为:

相应地可以简化为

式中D是语料中所有单词和上下文的集合。
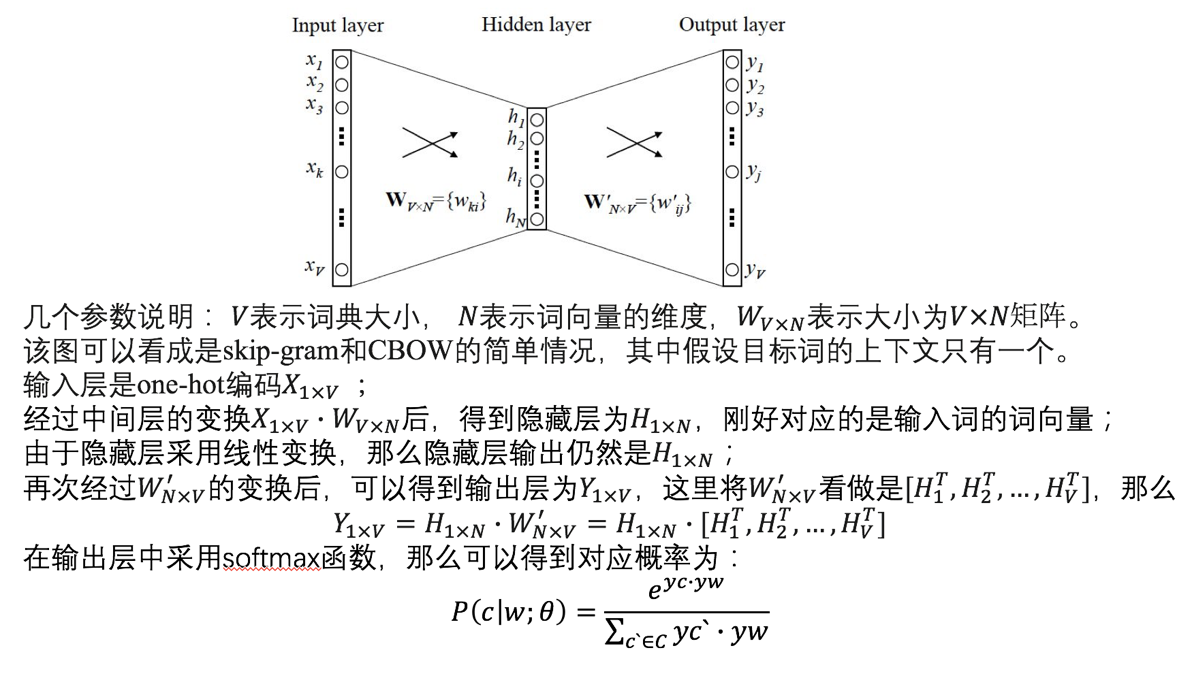
如果我们采用softmax函数的话,那么我们可以得到对应每个上下文的概率大小为:
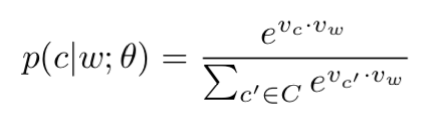
其中Vc和Vw可以看成是对应词c和词w的词向量。关于如何得到这个式子可以参考后面,那么将该式子代入上式并取log可以得到:
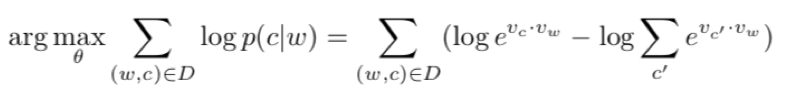
对上述目标函数求最大化,可以让相似的词具有相似的向量值。
3、采用负采样的目标函数
但是对上述目标函数进行优化,第二项需要对词典里的所有词进行优化,所以计算量比较大。如果换个角度考虑,如果我们将正常的上下问组合看成是1,不正常的上下文组合看成是0,那么问题转换为二分类问题,那么我们目标就是最大化下面的目标函数。

将输出层的softmax函数改为sigmoid函数,那么
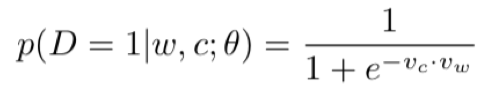
同样代入上式可以得到
但是这个目标函数存在问题,如果Vc=Vw,并且VcxVw足够大的话,就能取到最大值,这样所有词向量都是一样的,得到的词向量没有意义。所以考虑负采样,即引入负样本,那么
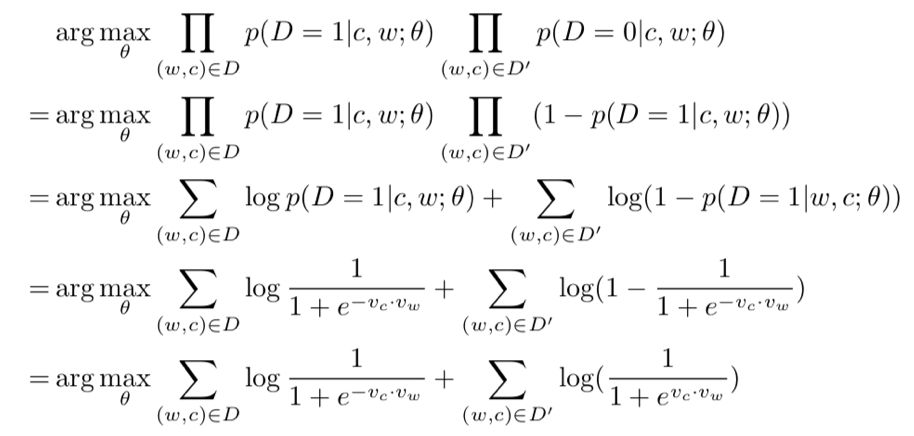
令
那么得到
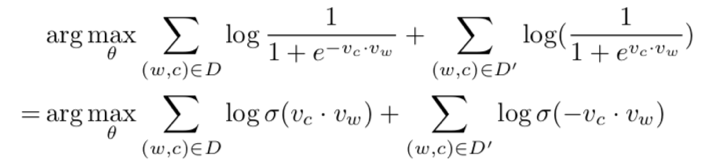
则与Mikolov提出的式子是一致的。
4、如何推导得到目标函数
5、举例
以“今天|天气|非常|不错|啊”举例,假设上下文只有一个词,选择目标词是“天气”,那么出现的情况有:
今天|天气,非常|天气,不错|天气,啊|天气
由于我们假设上下文只有一个词,那么在这些情况中只有【今天|天气,非常|天气】是正确的样本。
当我们采用【今天|天气】这个样本时,我们希望输入【天气】,会输出标签【今天】,其他概率都是0。
对于原始的skip-gram模型来说,这对应是一个4分类问题,当输入【今天|天气】时,那么我们可能出现的概率是P(今天|天气)、P(非常|天气)、P(不错|天气)和P(啊|天气),我们的目标就是让P(今天|天气)这个概率最大,但是我们得同时计算其他三类的概率,并在利用反向传播进行优化的时候需要对所有词向量都进行更新。这样计算量很大,比如我们这里就要更新5*100=500个参数(假设词向量维度是100维的)。
但是如果采用负采样,当输入【今天|天气】时,我们从【非常|不错|啊】中选出1个进行优化,比如【不错|天气】,即我们只需计算P(D=1|天气,今天)和P(D=0|天气,不错),并且在更新的时候只更新【不错】、【天气】和【今天】的词向量,这样只需更新300个参数,计算量大大减少了。
6、参考资料
[1]word2vec Parameter Learning Explained
[2]word2vec Explained: Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method
[3]Note on Word Representation
[4]Distributed Representations of Words and Phrases and their Compositionality