软件工程实践2019第三次作业

1.Github项目地址

https://github.com/1435738253/hello-world/tree/master/031702101

2.PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	20	15
Estimate	估计这个任务需要多少时间	30	20
Development	开发	300	210
Analysis	需求分析 (包括学习新技术)	100	50
Design Spec	生成设计文档	60	30
Design Review	设计复审	60	20
Coding Standard	代码规范 (为目前的开发制定合适的规范)	160	100
Design	具体设计	160	40
Coding	具体编码	200	300
Code Review	代码复审	30	10
Test	测试（自我测试，修改代码，提交修改）	100	70
Reporting	报告	50	100
Test Repor	测试报告	30	20
Size Measurement	计算工作量	30	10
Postmortem & Process Improvement Plan	事后总结, 并提出过程改进计划	30	20
合计		1360	1015

3.解题思路

写在前面
由于太久没进行代码相关练习，复健极为艰难，即使查了大量资料，使用文件输入输出还是有些不解，最后请教了班上大佬才整出来。
关于数独的解法，我一开始的想法是遍历+判断，但很明显，这样太浪费资源，于是在论坛上搜索数独发现了更好的办法——回溯法。翻了几篇博客之后，决定使用这种选优搜索算法来解决这道题目。
浏览并学习的几篇文章链接我会放在最后哒。

百度百科简介：

数独盘面是个九宫，每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次，所以又称“九宫格”。

首先给出解法的主体，利用回溯的思想。

void backtrace(int n)//回溯法进行填数
{
	int i;
	if (n == m * m)//满了就完成填数
	{
		output();//输出结果
		return;
	}
	int row = n / m;
	int col = n % m;
	if (a[row][col] == 0)
	{
		for (i = 1; i <= m; i++)
		{
			if (check(n,i))//可以填数
			{
				a[row][col] = i;
				backtrace(n + 1);//进入下一层函数
				a[row][col] = 0;//回溯
			}
		}
	}
	else
	{
		backtrace(n + 1);//进入下一层函数
	}
}

根据介绍，可以看出填数时需要验证行列以及宫内是否重复，由此
由于357宫格不用验证宫，4689需要验证，check()函数中需要一个判断是否验证宫的小小部分，然后若需要验证，则调用check_gong()函数进行验证。

下面给出check函数和检验宫的check_gong函数

bool check(int n,int x)//行和列的验证
{
	int row = n / m;
	int col = n % m;
	int i, j, k=1;
	for (i = 0; i < m; i++)//验证行
	{
		if (a[row][i] == x) return false;
	}
	for(j = 0; j<m; j++)//验证列
	{
		if (a[j][col] == x) return false;
	}
	//判断是否需要验证宫
	if (m == 4) k = check_gong(n, x, 2, 2);
	else if (m == 6) k = check_gong(n, x, 2, 3);
	else if (m == 8) k = check_gong(n, x, 4, 2);
	else if (m == 9) k = check_gong(n, x, 3, 3);
	if(k==1) return true;
	else return false;
}

bool check_gong(int n, int x, int row, int col)//验证宫
{
	int i, j;
	int r = n / m;
	int c = n % m;
	r = r / row * row;
	c = c / col * col;
	for (i = r; i < (r + row); i++)
	{
		for (j = c; j < (c + col); j++)
		{
			if (a[i][j] == x) return false;
		}
	}
	return true;
}

下面给出3宫格到9宫格的输入输出文件截图

3宫格

4宫格

5宫格

6宫格

7宫格

8宫格

9宫格

经过Code Quality Analysis工具的分析

Studio Profiling Tools测试有问题，出不来全部，目前的部分如下

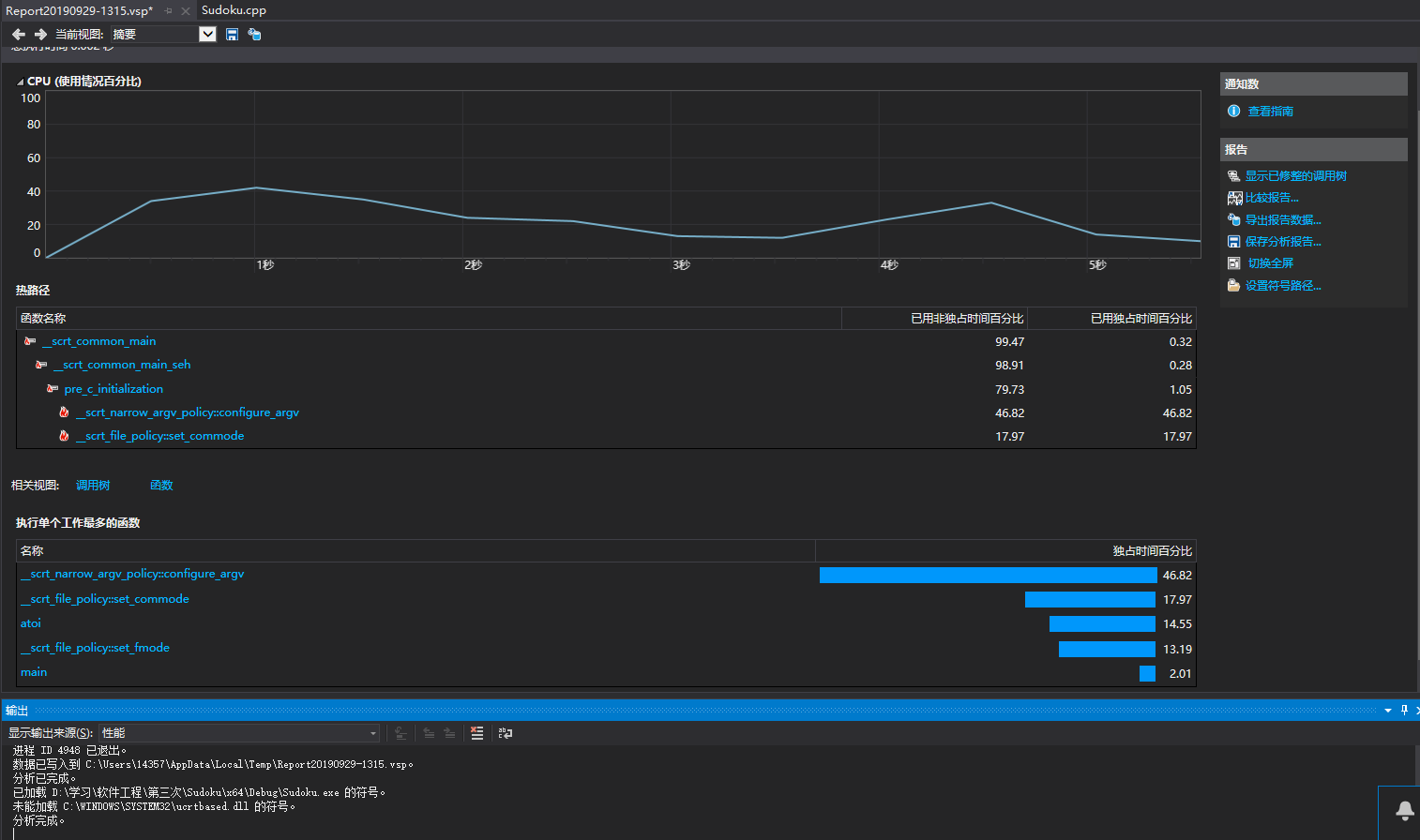
总结

总体来说最难的点我觉得是文件的输入输出，也稍微明白了一些vs的用法，但是还是有很多遗留问题需要解决，继续完善吧。

附学习资料：
求解数独（回溯法）
回溯法求解数独（C++实现）
递归回溯求解数独 C++实现方法
数独算法-递归与回溯
ofstream和ifstream详细用法